The Painter's Secret Geometry

A Study of Composition in Art

Charles Bouleau

• Verlag: Dover Publications
• Jahr: 2014
• ISBN:
  9780486795508
• Thema: Arte
• Thema: Técnicas artísticas

`This is an outstanding text for teachers and students.` — The Studio
This richly illustrated examination of visual arts in the European tradition shows how the great masters employed the `golden mean` and other geometrical patterns to compose their paintings. Author Charles Bouleau explores a tremendous variety of ancient and modern works: the Parthenon friezes, Italian mosaics, the Bayeux Tapestry, and Gothic stonemasons' marks of France and Germany as well as paintings by Picasso, Kandinsky, Klee, and Pollock. His insightful expositions cast new light on such well-known works as Raphael's `The School of Athens,` Botticelli's `Birth of Venus,` Rubens' `Descent from the Cross,` and Renoir's `Le Moulin de la Galette.`
Advancing step by step through each painter's vast body of work, the survey highlights new contributions from each period and artist. Every analysis is conducted according to strict methods, placing the work within the intellectual atmosphere of its time. Original, informative, and stimulating, The Painter's Secret Geometry reveals the framework of art as well as its most profound and secret poetry. This new edition of the cult classic is a vade mecum for any student of art history or artistic composition.
`I found the material presented in this book to be fascinating. Though originally published in the 1960's it's tenets hold up well. It would lend itself well to an art history course or to anyone interested in the concepts outlines.` — Tacoma Public Library

IV THE MUSICAL CONSONANCES

Raphael: School of Athens, detail. Pythagoras explaining the musical consonances with a diagram. (Rome, Vatican. Photo Anderson)

We come now to the generation of artists who lived at Florence or in Northern Italy in the middle of the fifteenth century and are known as the artists of the early Renaissance. Their period has also been called the age of humanism: some of these artists, with minds far above the ordinary, enthusiastic and incapable of keeping their discoveries to themselves, not only showed themselves innovators in their works but also expressed their thoughts in books that had a profound effect on their contemporaries. They were pioneers, theorists: Alberti, Serlio and Palladio for architecture, and Piero della Francesca for painting.

In his excellent book Architectural Principles in the Age of Humanism¹, Rudolf Wittkower says with great wisdom: ‘…in trying to prove that a system of proportions has been deliberately applied by painter, sculptor or architect, one is easily misled into finding in a given work those ratios which one sets out to find. Compasses in the scholar’s hand do not revolt. If we want to avoid the pitfall of useless speculation we must look for practical prescriptions of ratios supplied by the artists themselves. Curiously enough, that has never been done systematically.’ Let us try to apply to pictorial composition this admirable method applied by Wittkower to architecture, taking our stand, in the case of Piero della Francesca, on his own works and, more generally, as regards the whole of that generation, on the work of Alberti, which is just as essential in regard to painting as it is to architecture.

What is it that we find in these books? More mathematics. The prestige of mathematics is far from having diminished. As in the Middle Ages, men still traced that science back to Pythagoras through Plato’s Timaeus and looked to it for the secret meaning of the universe; but the knowledge of it had now become much more precise, and it was, above all, not now the same kind of mathematics. In the Middle Ages all research had been done with the compass-point. This had made possible a daily use of incommensurable quantities and, in particular, of the golden ratio—practical geometry in conformity with methods of working and studio tricks embellished by a mystical philosophy but still, after all, a labour of craftsmen. In contrast, the humanist generation plunged into books: it studied the Timaeus in Ficino’s commentary, of which printed editions were becoming available; it recovered direct access to Euclid, Vitruvius and Ptolemy, and looked for the distant Pythagoras in books on musical theory like that of Boethius. The result was, first, precision—clear ideas and exact numerical calculations; and in consequence less and less liking for compass-drawn figures that could not be calculated, and a growing taste for simple ratios. Wittkower² has shown what is the deep reason for this taste for simple, measurable relationships: it was the desire to attach the plastic arts to the major art, music, by the use of musical relationships.

Albertism

Any study of the period must start from Alberti: one cannot seriously try to recover the state of mind and tastes of that generation without reading his three books—the De re aedificatoria, published in Latin at Florence in 1485, the De statua and the De pictura. Their effect was considerable.

The latter book, though written in 1436, was not published till the sixteenth century; but it very quickly circulated in the artists’ studios in manuscript copies or extracts and was certainly known to Piero della Francesca, who drew inspiration from it in his Prospectiva pingendi. The De re aedificatoria, which was also known long before it was published, had an even wider influence. It is a treatise on architecture, but some of its chapters on proportion and on ornament are of interest to all artists, and the tone of the book, the peculiarly calm and serene aesthetic that emerges from it, awakened great sympathy in the painters.

Leaving aside the first books, devoted to problems that are largely technical (ground-plans, building materials, the organization of the work, etc.), let us look at book IX, which treats of the adornment of buildings. Here the conditions of beauty are laid down in a most precise way. In chapter V Alberti explains that the musical intervals agreeable to the ear, the octave, fifth and fourth, correspond to the division of a string in 2, in 3, or in 4 (1/2, 2/3, 3/4). These proportions, known at the time as the diapason, diapente and diatessaron, will also serve as bases for the plastic arts, and first of all for architecture. This is then studied in detail in chapter VI³, which treats of surfaces:

The ’short areas’ will be square, or 2/3, or 3/4. If one of the dimensions has to be longer than the other, twice these proportions will be taken, that is to say twice 2/3, which gives, if we start from 4 as the small side, 4, 6, 9 for the large side (4/6 = 6/9 = 2/3); or else twice 3/4, which gives, if we start from 9/9, 12, 16 (9/12 = 12/16 = 3/4).

Or again, one may simply take the ratio 1/2, the octave or diapason, not forgetting that the octave is made up of the fifth and fourth, or of the fourth and fifth. The former combination will divide the wall like this: 4, 6, 8 (4/6 or the fifth, and 6/8 or the fourth); the latter will divide it, for instance, like this: 3, 4, 6 (3/4 or the fourth, 4/6 or the fifth).

These proportions can be doubled or combined, but without ever exceeding the number 27, the third cube, for the Ancients observed that the mathematical laws of music were valid only for the small numbers.

Finally, Alberti recommends sticking to a single ratio: if in a building the length is twice the breadth, we shall not use for the height ratios deriving from the triple proportion…⁴

This analysis will become clearer if we refer to the text of Alberti’s De re aedificatoria, book IX. In chapter V of this book, Alberti expounds the theory of the musical relationship. Here are the salient points:

—The Diapason, octave or double: ‘The Numbers answer to one another in a double Proportion, as two to one, or the Whole to the Half.’ (Octave =1/2)

—The Diapente, fifth or sesquialtera: ‘The String which produced it bore the same Proportion to that to which it is compared, as one and an half does to one… The longer String must be allowed three, and the shorter, two.’ (Fifth = 2/3)

—The Diatessaron, fourth or sesquitertia: ‘…where the longer String contains the shorter one and one third more.’ (Fourth = 3/4)

—The Diapason-Diapente or triple: ‘They answer as three to one, or as the Whole to one third of itself.’ (1/2 × 2/3 = 1/3)

—The Tonus, ‘which was also called the Sesquioctave…, wherein the long String compared to shorter, exceeds it one eighth part of the shorter String.’ (1/8)⁵

‘Of all these Numbers,’ Alberti comments, ‘the Architects made very convenient Use, taking them sometimes two by two, as in planning out their Squares and open Areas…’

In chapter VI Alberti applies this theory to architectural ground-plans, or ‘areas’. He says:

‘Of these Proportions we are now to treat more particularly, and first we shall say something of those Areas where only two⁶ are used.

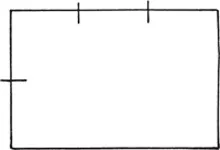
‘Of Areas, some are short, some long, and some between both. The shortest of all is the perfect Square, every Side whereof is of equal Length, all corresponding with one another at Right Angles. The nearest to this is the Sesquialtera, and the Sesquitertian also may be reckoned among the Shorter Areas.’ (figs. 1 and 2)

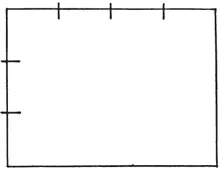
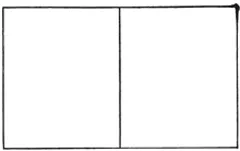
‘These three Proportions therefore, which we may also call simple, are proper for the smaller Platforms. There are likewise three others, which are proper for middling Platforms: The best of all is the Double (fig. 3), and the next best is that which is formed of the Sesquialtera doubled (fig. 4), which is produced as follows: Having set down the least Number of the Area, as, for instance, four, lengthen it to the first Sesquialtera, which will make six, and then add the Sesquialtera of this six, which will produce nine⁷. Thus the Length will exceed the Breadth in a double Proportion, and one Tone more⁸.’

Figure 1: Sesquialtera (Diapente 2/3).

Figure 2: Sesquitertia (Diatessaron 3/4).

Figure 3: Double (Diapason 1/2).

Figure 4: Double sesquialtera (Double diapente 4/6/9).

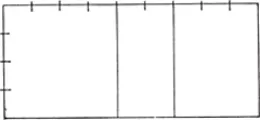
Figure 5: Double sesquitertia (Double diatessaron 9/12/16).

‘For moderate Platforms also; we may use that Proportion which arises from the Sesquitertian doubled in the same Manner as the former (fig. 5); where-in the Length and Breadth will be as nine and sixteen⁹. Here the longer Line contains the shorter twice, excluding one Tone¹⁰.’

‘In the longest Areas we either add the Duple to the Sesquialtera, which will produce the Triple¹¹ (fig. 6); or add the Sesquitertia to the Duple, which will make the Proportion as three to eight¹²; or lastly make the Lines correspond to each other in a Quadruple Proportion.’

The Renaissance artists took Alberti’s text literally, preferring to base their practice on the numbers given by him as examples, and even marking them in their diagrams¹³. The ‘mean areas’ were particularly right for the painters, who therefore took a special interest in the ratios 4/6/9 and 9/12/16. The ‘long areas’ were of little use to them, since their proportions rarely corresponded to those of a picture.

We are here a long way from Pacioli’s book, in which a certain proportion, called ‘divine’, was held up to admiration precisely because it was incommensurable. Here, on the contrary, beauty resides in the relations between the first whole numbers, simple relationships easily read at a glance and always measurable. Not just any relationships, it is true, but only those that are found in the musical scale: the resulting aesthetic is different from that of Pacioli, but the inte...