
Elements of Fluid Dynamics
Guido Buresti
- 604 páginas
- English
- ePUB (apto para móviles)
- Disponible en iOS y Android
Elements of Fluid Dynamics
Guido Buresti
Información del libro
Elements of Fluid Dynamics is intended to be a basic textbook, useful for undergraduate and graduate students in different fields of engineering, as well as in physics and applied mathematics. The main objective of the book is to provide an introduction to fluid dynamics in a simultaneously rigorous and accessible way, and its approach follows the idea that both the generation mechanisms and the main features of the fluid dynamic loads can be satisfactorily understood only after the equations of fluid motion and all their physical and mathematical implications have been thoroughly assimilated. Therefore, the complete equations of motion of a compressible viscous fluid are first derived and their physical and mathematical aspects are thoroughly discussed. Subsequently, the necessity of simplified treatments is highlighted, and a detailed analysis is made of the assumptions and range of applicability of the incompressible flow model, which is then adopted for most of the rest of the book. Furthermore, the role of the generation and dynamics of vorticity on the development of different flows is emphasized, as well as its influence on the characteristics, magnitude and predictability of the fluid dynamic loads acting on moving bodies.
The book is divided into two parts which differ in target and method of utilization. The first part contains the fundamentals of fluid dynamics that are essential for any student new to the subject. This part of the book is organized in a strictly sequential way, i.e. each chapter is assumed to be carefully read and studied before the next one is tackled, and its aim is to lead the reader in understanding the origin of the fluid dynamic forces on different types of bodies. The second part of the book is devoted to selected topics that may be of more specific interest to different students. In particular, some theoretical aspects of incompressible flows are first analysed and classical applications of fluid dynamics such as the aerodynamics of airfoils, wings and bluff bodies are then described. The one-dimensional treatment of compressible flows is finally considered, together with its application to the study of the motion in ducts.
Sample Chapter(s)
Chapter 1: Introduction (133 KB)
Request Inspection Copy
Contents:
- Fundamentals:
- Introduction
- Properties of Fluids
- Characterization of the Motion of Fluids
- The Equations of Motion of Fluids
- The Incompressible Flow Model
- Vorticity Dynamics in Incompressible Flows
- Incompressible Boundary Layers
- Fluid Dynamic Loads on Bodies in Incompressible Flows
- Deeper Analyses and Classical Applications:
- Exact Solutions of the Incompressible Flow Equations
- The Role of the Energy Balance in Incompressible Flows
- Supplementary Issues on Vorticity in Incompressible Flows
- Airfoils in Incompressible Flows
- Finite Wings in Incompressible Flows
- An Outline of Bluff-Body Aerodynamics
- One-Dimensional Compressible Flows
Readership: Graduates and undergraduates in the fields of fluid mechanics and engineering, specifically aerospace, mechanical and civil engineering.
Preguntas frecuentes
Información
INCOMPRESSIBLE FLOW EQUATION
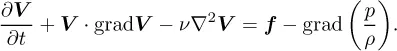 | (9.1) |
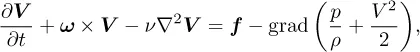 | (9.2) |
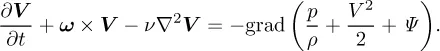 | (9.3) |
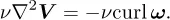 | (9.4) |