Structural Dynamic Analysis with Generalized Damping Models

Identification

Sondipon Adhikari

• Publisher: Wiley-ISTE
• Year: 2014
• ISBN:
  9781118863022
• Edition: 1
• Topic: Technology & Engineering
• Subtopic: Aeronautic & Astronautic Engineering
• Index: Technology & Engineering

Since Lord Rayleigh introduced the idea of viscous damping in his classic work "The Theory of Sound" in 1877, it has become standard practice to use this approach in dynamics, covering a wide range of applications from aerospace to civil engineering. However, in the majority of practical cases this approach is adopted more for mathematical convenience than for modeling the physics of vibration damping.
Over the past decade, extensive research has been undertaken on more general "non-viscous" damping models and vibration of non-viscously damped systems. This book, along with a related book Structural Dynamic Analysis with Generalized Damping Models: Analysis, is the first comprehensive study to cover vibration problems with general non-viscous damping. The author draws on his considerable research experience to produce a text covering: parametric senistivity of damped systems; identification of viscous damping; identification of non-viscous damping; and some tools for the quanitification of damping. The book is written from a vibration theory standpoint, with numerous worked examples which are relevant across a wide range of mechanical, aerospace and structural engineering applications.

Contents

1. Parametric Sensitivity of Damped Systems.
2. Identification of Viscous Damping.
3. Identification of Non-viscous Damping.
4. Quantification of Damping.

About the Authors

Sondipon Adhikari is Chair Professor of Aerospace Engineering at Swansea University, Wales. His wide-ranging and multi-disciplinary research interests include uncertainty quantification in computational mechanics, bio- and nanomechanics, dynamics of complex systems, inverse problems for linear and nonlinear dynamics, and renewable energy. He is a technical reviewer of 97 international journals, 18 conferences and 13 funding bodies.He has written over 180 refereed journal papers, 120 refereed conference papers and has authored or co-authored 15 book chapters.

Chapter 1

Parametric Sensitivity of Damped Systems

Changes of the eigenvalues and eigenvectors of a linear vibrating system due to changes in system parameters are of wide practical interest. Motivation for this kind of study arises, on the one hand, from the need to come up with effective structural designs without performing repeated dynamic analysis, and, on the other hand, from the desire to visualize the changes in the dynamic response with respect to system parameters. Furthermore, this kind of sensitivity analysis of eigenvalues and eigenvectors has an important role to play in the area of fault detection of structures and modal updating methods. Sensitivity of eigenvalues and eigenvectors is useful in the study of bladed disks of turbomachinery where blade masses and stiffness are nearly the same, or deliberately somewhat altered (mistuned), and one investigates the modal sensitivities due to this slight alteration. Eigensolution derivatives also constitute a central role in the analysis of stochastically perturbed dynamical systems. Possibly, the earliest work on the sensitivity of the eigenvalues was carried out by Rayleigh [RAY 77]. In his classic monograph, he derived the changes in natural frequencies due to small changes in system parameters. Fox and Kapoor [FOX 68] have given exact expressions for the sensitivity of eigenvalues and eigenvectors with respect to any design variables. Their results were obtained in terms of changes in the system property matrices and the eigensolutions of the structure in its current state, and have been used extensively in a wide range of application areas of structural dynamics. Nelson [NEL 76] proposed an efficient method to calculate an eigenvector derivative, which requires only the eigenvalue and eigenvector under consideration. A comprehensive review of research on this kind of sensitivity analysis can be obtained in Adelman and Haftka [ADE 86]. A brief review of some of the existing methods for calculating sensitivity of the eigenvalues and eigenvectors is given in section 1.6 (Chapter 1, [ADH 14]).

The aim of this chapter is to consider parametric sensitivity of the eigensolutions of damped systems. We first start with undamped systems in section 1.1. Parametric sensitivity of viscously damped systems is discussed in section 1.2. In section 1.3, we discuss the sensitivity of eigensolutions of general non-viscously damped systems. In section 1.4, a summary of the techniques introduced in this chapter is provided.

1.1. Parametric sensitivity of undamped systems

The eigenvalue problem of undamped or proportionally damped systems can be expressed by

[1.1]

where λ_j and x_j are the eigenvalues and the eigenvectors of the dynamic system.

and

, the mass and stiffness matrices, are assumed to be smooth, continuous and differentiable functions of a parameter vector

. Note that λ_j =

where ω_j is the jth undamped natural frequency. The vector p may consist of material properties, e.g. mass density, Poisson’s ratio and Young’s modulus; or geometric properties, e.g. length, thickness and boundary conditions. The eigenvalues and eigenvectors are smooth differentiable functions of the parameter vector p.

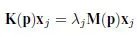
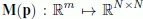
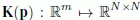
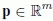
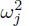
1.1.1. Sensitivity of the eigenvalues

We rewrite the eigenvalue equation as

[1.2]

[1.3]

The functional dependence of p is removed for notational convenience. Differentiating the eigenvalue equation [1.2] with respect to the element p of the parameter vector we have

[1.4]

Premultiplying by

, we have

[1.5]

Using the identity in [1.3], we have

[1.6]

[1.7]

Note that when the modes are mass normalized,

Mx_j = 1. Equation [1.7] shows that the derivative of a given eigenvalue depends only on eigensolutions corresponding to that particular eigenvalue. Next, we show that this fact is not true when we consider the derivative of the eigenvectors.

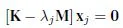
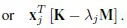
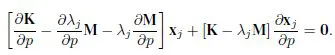
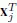
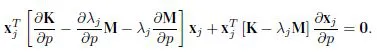
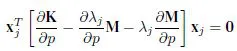
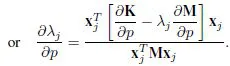
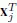
1.1.2. Sensitivity of the eigenvectors

Different methods have been developed to calculate the derivatives of the eigenvectors. One way to express the derivative of an eigenvector is by a linear combination of all the eigenvectors

[1.8]

This can always be done as x_r, r = 1,2, …, N forms a complete basis. It is necessary to find expressions for the constant a_jr for all r = 1,2, … N. Substituting this in equation [1.4], we have...