Mathematics of the Financial Markets

Financial Instruments and Derivatives Modelling, Valuation and Risk Issues

Alain Ruttiens

• Publisher: Wiley
• Year: 2013
• ISBN:
  9781118513484
• Edition: 1
• Topic: Business
• Subtopic: Finance
• Index: Business

Mathematics of the Financial Markets
Financial Instruments and Derivatives Modeling, Valuation and Risk Issues

"Alain Ruttiens has the ability to turn extremely complex concepts and theories into very easy to understand notions. I wish I had read his book when I started my career!"
Marco Dion, Global Head of Equity Quant Strategy, J.P. Morgan

"The financial industry is built on a vast collection of financial securities that can be valued and risk profiled using a set of miscellaneous mathematical models. The comprehension of these models is fundamental to the modern portfolio and risk manager in order to achieve a deep understanding of the capabilities and limitations of these methods in the approximation of the market. In his book, Alain Ruttiens exposes these models for a wide range of financial instruments by using a detailed and user friendly approach backed up with real-life data examples. The result is an excellent entry-level and reference book that will help any student and current practitioner up their mathematical modeling skills in the increasingly demanding domain of asset and risk management."
Virgile Rostand, Consultant, Toronto ON

"Alain Ruttiens not only presents the reader with a synthesis between mathematics and practical market dealing, but, more importantly a synthesis of his thinking and of his life."
René Chopard, CEO, Centro di Studi Bancari Lugano, Vezia / Professor, Università dell'Insubria, Varese

"Alain Ruttiens has written a book on quantitative finance that covers a wide range of financial instruments, examples and models. Starting from first principles, the book should be accessible to anyone who is comfortable with trading strategies, numbers and formulas."
Dr Yuh-Dauh Lyuu, Professor of Finance & Professor of Computer Science & Information Engineering, National Taiwan University

Part I

The Deterministic Environment

1

Prior to the yield curve: spot and forward rates

1.1 INTEREST RATES, PRESENT AND FUTURE VALUES, INTEREST COMPOUNDING

Consider a period of time, from t0 to t, in Figure 1.1.

Figure 1.1 Interest on a period of time, from t0 to t

$1 invested (or borrowed) @ i from t0 up to t gives $A. t is the maturity or tenor of the operation. $1 is called the present value (PV), and $A the corresponding future value (FV). i represents the interest rate or yield.

In this basic operation, no interest payment is made between t0 and t: in such a case, i is called a “0-coupon rate” or “zero” in short. Zeroes are also called “spot rates” as they refer to currently prevailing rates (at t0). Let us denote zt the current zero for a maturity t.

In the financial markets, the unit period of time is the year, and the interest rates, or yields, are expressed in percent per annum (% p.a.), that is, per year. In the US market, interest rates may also be expressed on a semi-annual basis (s.a.) with respect to the market of US bonds paying semi-annual coupons. Database providers, such as Bloomberg or Reuters, do well in always specifying whether the rates they mention are expressed on an annual or a semi-annual basis.

If the maturity t = 1 year, and z1 the corresponding zero rate expressed in % p.a., the relationship between PV and FV is

(1.1)

meaning that the future value FV is the sum of the present value PV plus the interest computed on PV @ z1, that is, PV × z1.

If the maturity t is shorter than 1 year, the interest is computed pro rata temporis, t being counted as a fraction of a year. Equation 1.1 becomes

(1.2)

The time unit period of 1 year is a natural compounding time unit, that is, above 1 year, interests must be compounded (see the following). On the US market, the compounding time unit is normally 0.5 years.

If t > 1 year for zeroes expressed on an annual basis, or >0.5 year for zeroes expressed on a semi-annual basis,

• 
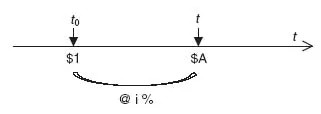
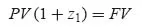
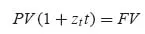
  either t is a round number of years (or of half-years in the case of semi-annual basis), Eq. 1.1 becomes

(1.3)

that is, zt is compounded t times. Indeed, suppose that t = 2 years. Since for a zero-coupon there are no cash flows (of interest) paid between t0 and year 2, the interest relating to the first year is compounded so that, for the second year, the present value at the beginning of year 2 becomes

and earns interest @ z2 during the second year so that

In the case of compounding of s.a. rates, Eq. 1.3 becomes

And, more generally, if the zero rates were to be compounded n times a year,

(1.4)

• 
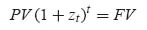
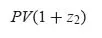
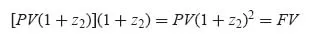
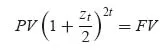
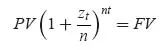
  or t is not a round number of years, for example t = n years + t′. In this case the market practice consists of combining both rules (Eq. 1.2 and Eq. 1.3):

1.1.1 Counting the number of days

The rules for expressing t differ from one market to another: fractions of a year may be counted as a number of days nd that can be based on the actual (ACT) number of days, or on full months of 30 days plus actual number of days for a fraction of a month, the year being counted as a 360-days or a 365-days year, to follow the most usual conventions.

The market practice uses the following day count conventions:

In USD:

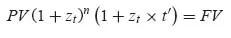
• on the money market (cf. Section 2.1): ACT/360, that is, the actual number of days, divided by (a year of) 360 days;
• on longer maturities: USD swap rates ¹: 30/360 (semi-annual), US government Treasury bonds: ACT/365 (semi-annual).

In EUR:

• on the money market: ACT/360;
• on longer maturities: EUR swap rates: 30/360, EUR sovereign bonds: ACT/ACT.

The set of zts, or {zt}, is called the term structure of interest rates, or the yield curve. Strictly speaking, this wording should apply only to spot or zero-coupon interest rates, and not to usual bond yields.

The set {zt} plays a key role in financial calculus, especially for pricing interest rate products, such as bonds, or instruments such as derivatives. Indeed, these instruments are anything but combinations of cash flows to be paid or received on some future dates, so that to value them at the current time, one needs to compute the present value of any future cash flows involved, by ...