Mathematik und Statistik in der Finanzwirtschaft

Grundlagen - Anwendungen - Fallstudien

Reinhold Hölscher, Christian Kalhöfer

• Publisher: De Gruyter Oldenbourg
• Year: 2015
• Print ISBN: 9783486716481
• eBook ISBN: 9783110398502
• Edition: 1
• Topic: Economics
• Subtopic: Economic Theory
• Index: Economics

Die Beschäftigung mit finanzwirtschaftlichen Fragestellungen erfordert heute mehr denn je fundierte mathematische Kenntnisse – nicht nur im Rahmen der betrieblichen Finanzwirtschaft, sondern auch im Umgang mit privaten Investitions- und Finanzierungsentscheidungen sowie für Kundenberater in der Finanzdienstleistungsindustrie. Das Buch entwickelt das notwendige Wissen, das von finanzmathematischen Standards der Zins-, Barwert- und Effektivzinsrechnung bis zum modernen Risikomanagement mit Elementen aus Portfoliotheorie, Optionspreisbestimmung sowie der Risikomessung mit dem Value at Risk reicht. Die dafür notwendigen Grundkenntnisse der Statistik werden ebenfalls vermittelt. Umfangreiche Beispiele erläutern die theoretischen Ansätze praxisbezogen. Zu jedem Kapitel gibt es umfassende Fallstudien, mit deren Hilfe ein Selbststudium möglich ist.

1 Zinsrechnung

1.1 Grundlagen und Verfahren

1.1.1 Die Notwendigkeit der Berücksichtigung von Zinsen

Zinsen stellen in der Geschäftswelt den Preis für die Überlassung von Kapital auf Zeit dar. Ein Gläubiger überlässt einem Schuldner für eine gewisse Zeitspanne einen bestimmten Kapitalbetrag, der dafür ein Entgelt in Form von Zinsen zu bezahlen hat. Die Existenz von Zinsen führt im Allgemeinen zu der Beobachtung, dass gleich hohe Zahlungen, die ein Wirtschaftssubjekt alternativ zu verschiedenen Zeitpunkten erhält bzw. leisten muss, nicht die gleiche Wertschätzung genießen.

Beispiel

Eine Einzahlung von 100 EUR am 1. Januar wird einer Einzahlung am 1. Januar des Folgejahres vorgezogen, denn bei der ersten Einzahlung könnten die 100 EUR für ein Jahr zinsbringend angelegt werden. Beträgt der Zinssatz beispielsweise 5%, dann hat die Einzahlung vom 1. Januar ein Jahr später einen Wert von 105 EUR. Im Vergleich zu der zweiten Alternative, einer Einzahlung in Höhe von 100 EUR am 1. Januar des Folgejahres, ist damit die frühere Einzahlung um 5 EUR vorteilhafter.

Umgekehrt wird im Fall von Auszahlungen vorgegangen. Hierbei ist eine Auszahlung von 100 EUR am 1. Januar des Folgejahres natürlich einer Auszahlung von 100 EUR am 1. Januar vorzuziehen.

In allgemeiner Form kann also gesagt werden, dass bei gleicher Höhe der Zahlungen eine zeitlich frühere Einzahlung vorteilhafter als eine zeitlich spätere Einzahlung und eine zeitlich frühere Auszahlung unvorteilhafter als eine zeitlich spätere Auszahlung sind. Zahlungen, die zu verschiedenen Zeitpunkten anfallen, lassen sich nur durch Einbeziehung der Zinseffekte vergleichen. Diese Aussage gilt erst recht, wenn die Zahlungen nicht gleich groß sind, sondern unterschiedliche Beträge aufweisen oder wenn es sich dabei um ganze Zahlungsreihen, d. h. mehrere Zahlungen zu unterschiedlichen Zeitpunkten handelt.

Wenn in diesem Zusammenhang von Vorteilhaftigkeit die Rede ist, dann stellt sich die Frage, von welchen Faktoren denn die Höhe des Vorteils abhängig ist. Mit anderen Worten geht es um die Frage der Berechnung der Zinsen. Die Höhe eines (absoluten) Zinsbetrages hängt bei feststehendem Zinssatz im Wesentlichen von drei Faktoren ab:

• Der erste Einflussfaktor ist natürlich der Zeitraum, für den Zinsen gezahlt werden, z. B. die Laufzeit eines Kredites in Jahren.
• Der zweite Einflussfaktor ist der Abstand zwischen den Zinszahlungen, die sogenannte Zinsperiode. Hier wird also beispielsweise berücksichtigt, ob die Zinsen jährlich, halbjährlich oder vierteljährlich gezahlt werden.
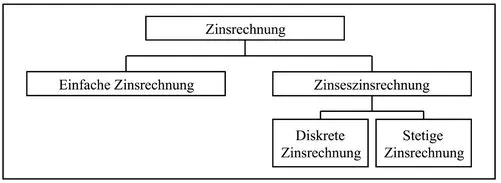
• Der dritte Einflussfaktor ist die Berücksichtigung bereits angefallener Zinsen. In diesem Zusammenhang werden zwei Formen der Zinsrechnung unterschieden. Bei der einfachen Zinsrechnung werden die angefallenen Zinsen nicht mit verzinst, während bei der Zinseszinsrechnung die angefallenen Zinsen in die Berechnung einbezogen werden, d. h. sie werden mit verzinst. Wie die folgende Abbildung 1.1 verdeutlicht, kann bei der Zinseszinsrechnung des Weiteren zwischen der diskreten und der stetigen Form der Zinsrechnung unterschieden werden.

Abbildung 1.1: Verfahren der Zinsrechnung

Bevor die verschiedenen Verfahren der Zinsrechnung erläutert werden, müssen noch die wichtigsten in den Folgekapiteln verwendeten finanzmathematischen Abkürzungen erläutert werden.

Um in der Finanzmathematik allgemeingültige Formeln aufstellen zu können, wird nicht mit konkreten Jahreszahlen gearbeitet, sondern es erfolgt eine Indizierung der Zahlungszeitpunkte. Die erste Zahlung fällt normalerweise zum Zeitpunkt 0 an, die betrachtete Laufzeit wird mit n bezeichnet. Zwischenzeitliche Zahlungszeitpunkte tragen den Laufindex j. Auf einem Zeitstrahl (vgl. Abbildung 1.2) lässt sich dieser Sachverhalt veranschaulichen.

Abbildung 1.2: Zeitstrahl

Auch für die Zinssätze und die Kapitalgrößen im Zeitablauf werden Symbole verwendet. Im Folgenden bezeichnen

• p den Nominalzins pro Zinsperiode in Prozent,
• i das Verhältnis p/100,
• q die Summe 1 + i,
• K₀ das Ausgangs- oder Startkapital zum Zeitpunkt 0,
• K_n das Endkapital nach n Zinsperioden,
• K_j den Zwischensaldo nach der j-ten Zinsperiode.

Bei der Angabe von Zinssätzen kann zwischen dem Nominal- und dem Effektivzins unterschieden werden. Dabei bezieht sich der Nominalzins immer auf den Nennwert des betrachteten Produkts, beispielsweise also des Kredits oder des festverzinslichen Wertpapiers. Als Nennwert wird in der Regel der Betrag bezeichnet, zu dem die Anlage bei Fälligkeit zurückgezahlt wird. Sofern Auszahlungs- und Rückzahlungsbetrag der Anlage übereinstimmen, ist die Angabe des Effektivzinssatzes (bei jährlicher Zahlungsweise) unproblematisch, denn Nominal-und Effektivzinssatz sind identisch. Ein Problem entsteht dann, wenn Auszahlungs- und Rückzahlungsbetrag nicht gleich groß sind, was in der Praxis durchaus häufig vorkommt. Für finanzmathematische Berechnungen ist i. d. R.. zunächst der Nominalzinssatz erforderlich. Der Nominalzins wird üblicherweise als Jahreszinssatz (p.a.) angegeben. Aus dem Nominalzinssatz kann unmittelbar der Zahlungsstrom eines Produktes hergeleitet werden.

Beispiel

Ein Unternehmer benötigt einen Kredit über 9.500 EUR für die Dauer von einem Jahr. Mit seiner Hausbank vereinbart er einen Kredit über 10.000 EUR zu einem Nominalzinssatz von 8%. Der Kreditvertrag enthält eine Vereinbarung über ein Disagio von 5%, d. h. der Unternehmer erhält eine Summe von 9.500 EUR ausgezahlt. Der Rückzahlungsbetrag ist allerdings 10.000 EUR, sodass Auszahlungs- und Rückzahlungsbetrag nicht identisch sind. Ferner muss der Unternehmer nach einem Jahr 800 EUR Zinsen zahlen. Ohne auf die Einzelh...

Table of contents

• Titel
• Impressum
• Vorwort
• Inhaltsverzeichnis
• Übersicht der Zeichnungen
• Übersicht der Tabellen
• 1 Zinsrechnung
• 2 Statistik
• 3 Beispiele finanzwirtschaftlicher Anwendungen
• 4 Anhang: Mathematische Grundlagen
• 5 Lösungsvorschläge
• Literaturverzeichnis
• Index