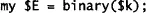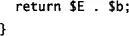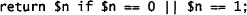Higher-Order Perl

Transforming Programs with Programs

Mark Jason Dominus

• Publisher: Morgan Kaufmann
• Year: 2005
• ISBN:
  9780080478340
• Topic: Informatica
• Subtopic: Programmazione

Most Perl programmers were originally trained as C and Unix programmers, so the Perl programs that they write bear a strong resemblance to C programs. However, Perl incorporates many features that have their roots in other languages such as Lisp. These advanced features are not well understood and are rarely used by most Perl programmers, but they are very powerful. They can automate tasks in everyday programming that are difficult to solve in any other way. One of the most powerful of these techniques is writing functions that manufacture or modify other functions. For example, instead of writing ten similar functions, a programmer can write a general pattern or framework that can then create the functions as needed according to the pattern. For several years Mark Jason Dominus has worked to apply functional programming techniques to Perl. Now Mark brings these flexible programming methods that he has successfully taught in numerous tutorials and training sessions to a wider audience.* Introduces powerful programming methods—new to most Perl programmers—that were previously the domain of computer scientists* Gradually builds up confidence by describing techniques of progressive sophistication* Shows how to improve everyday programs and includes numerous engaging code examples to illustrate the methods

CHAPTER 1 RECURSION AND CALLBACKS

The first “advanced” technique we’ll see is recursion. Recursion is a method of solving a problem by reducing it to a simpler problem of the same type.

Unlike most of the techniques in this book, recursion is already well known and widely understood. But it will underlie several of the later techniques, and so we need to have a good understanding of its fine points.

1.1 DECIMAL TO BINARY CONVERSION

Until the release of Perl 5.6.0, there was no good way to generate a binary numeral in Perl. Starting in 5.6.0, you can use sprintf (“%b”, $num), but before that the question of how to do this was Frequently Asked.

Any whole number has the form 2k + b, where k is some smaller whole number and b is either 0 or 1. b is the final bit of the binary expansion. It’s easy to see whether this final bit is 0 or 1; just look to see whether the input number is even or odd. The rest of the number is 2k, whose binary expansion is the same as that of k, but shifted left one place. For example, consider the number 37 = 2 · 18 + 1; here k is 18 and b is 1, so the binary expansion of 37 (100101) is the same as that of 18 (10010), but with an extra 1 on the end.

How did I compute the expansion for 37? It is an odd number, so the final bit must be 1; the rest of the expansion will be the same as the expansion of 18. How can I compute the expansion of 18? 18 is even, so its final bit is 0, and the rest of the expansion is the same as the expansion of 9. What is the binary expansion for 9? 9 is odd, so its final bit is 1, and the rest of its binary expansion is the same as the binary expansion of 4. We can continue in this way, until finally we ask about the binary expansion of 1, which of course is 1.

This procedure will work for any number. To compute the binary expansion of a number n we proceed as follows:

1. If n is 1, its binary expansion is 1, and we may ignore the rest of the procedure. Similarly, if n is 0, the expansion is simply 0. Otherwise:

2. Compute k and b so that n = 2k + b and b = 0 or 1. To do this, simply divide n by 2; k is the quotient, and b is the remainder, 0 if n was even, and 1 if n was odd.

3. Compute the binary expansion of k, using this same method. Call the result E.

4. The binary expansion for n is Eb.

Let’s build a function called binary() that calculates the expansion. Here is the preamble, and step 1:

Here is step 2:

For the third step, we need to compute the binary expansion of k. How can we do that? It’s easy, because we have a handy function for computing binary expansions, called binary() —or we will once we’ve finished writing it. We’ll call binary() with k as its argument:

Now the final step is a string concatenation:

This works. For example, if you invoke binary(37), you get the string 100101.

The essential technique here was to reduce the problem to a simpler case. We were supposed to find the binary expansion of a number n; we discovered that this binary expansion was the concatenation of the binary expansion of a smaller number k and a single bit b. Then to solve the simpler case of the same problem, we used the function binary() in its own definition. When we invoke binary() with some number as an argument, it needs to compute binary() for a different, smaller argument, which in turn computes binary() for an even smaller argument. Eventually, the argument becomes 1, and binary() computes the trivial binary representation of 1 directly.

This final step, called the base case of the recursion, is important. If we don’t consider it, our function might never terminate. If, in the definition of binary(), we had omitted the line:

then binary() would have computed forever, and would never have produced an answer for any argument.

1.2 FACTORIAL

Suppose you have a list of n different items. For concreteness, we’ll suppose that these items are letters of the alphabet. How many different orders are there for such a list? Obviously, the answer depends on n, so it is a function of n. This function is called the factorial function. The factorial of n is the number of different orders for a list of n different items. Mathematicians usually write it as a postfix (!) mark, so that the factorial of n is n!. They also call the different orders permutations.

Let’s compute some factorials. Evidently, there’s only one way to order a list of one item, so 1! = 1. There are two permutations of a list of two items: A-B and B-A, so 2! = 2. A little pencil work will reveal that there are six permutations of three items:

How can we be sure we didn’t omit anything from the list? It’s not hard to come up with a method that constructs every possible ordering, and in Chapter 4 we will see a program to list them all. Here is one way to do it. We can make any list of three items by adding a new item to a list of two items. We have two choices for the two-item list we start with: AB and BA. In each case, we have three choices about where to put the C: at the beginning, in the middle, or at the end. There are 2 · 3 = 6 ways to make the choices together, and since each choice leads to a different list of three items, there must be six such lists. The preceding left column shows all the lists we got by inserting the C into AB, and the right column shows the lists we got by inserting the C into BA, so the display is complete.

Similarly, if we want to know how many permutations there are of four items, we can figure it out the same way. There are six different lists of three items, and there are four positions where we could insert the fourth item into each of the lists, for a total of 6 · 4 = 24 total orders:

Now we’ll write a function to compute, for any n, how many permutations there are of a list of n elements.

We’ve just seen that if we know the number of possible permutations of n – 1 things, we can compute the number of permutations of n things. To make a list of n things, we take one of the (n – 1)! lists of n – 1 things and insert the nth thing into one of th...