La restituzione della geometria pitagorica

Arturo Reghini

• Publisher: Youcanprint
• Year: 2018
• eBook ISBN: 9788827809112
• Topic: Literature
• Subtopic: Literary Collections
• Index: Literature

Una delle opere base di Reghini, senza questi libri tanta parte delle opere di altri autori, non sarebbero neppure avvicinabili. INDICE: PREMESSE CAPITOLO I - L TEOREMA DEI DUE RETTI CAPITOLO II - IL TEOREMA DI PITAGORA CAPITOLO III - IL PENTALFA CAPITOLO IV - I POLIEDRI REGOLARI CAPITOLO V - IL SIMBOLO DELL'UNIVERSO CAPITOLO VI - DIMOSTRAZIONE DEL POSTULATO DI EUCLIDE

CAPITOLO IV - I POLIEDRI REGOLARI

I. Per vedere in quale modo Pitagora pervenne alla costruzione dei poliedri regolari ed alla loro inscrizione nella sfera occorrerebbe fare per lo spazio quel che abbiamo fatto, in parte, per il piano. Ossia ricostruire la geometria pitagorica dello spazio senza introdurre i concetti di rette parallele, di rette e piani paralleli, di piani paralleli, e mostrare come si possa egualmente pervenire ai risultati che Eudemo attraverso Proclo ci tramanda come conseguiti da Pitagora. Ma per non allungare troppo questo nostro studio ci limiteremo ad indicare per sommi capi la via da tenere, o una delle vie da seguire, tralasciando in generale le dimostrazioni che ognuno può trovare da sé.

Perciò, ammettendo che un piano divida lo spazio in due semispazii, ammettiamo anche il postulato del semispazio: Il segmento congiungente due punti situati da parti opposte rispetto ad un piano è tagliato in un suo punto dal piano. Può darsi che anche questo caso particolare del postulato di continuità fosse ammesso tacitamente come una verità primordiale. Si dimostra poi nel modo ordinario che:

a) Una retta non giacente in un piano e che abbia con esso un punto comune è divisa da esso in due semirette situate da parti opposte rispetto a quel piano.

b) Se due piani hanno un punto in comune la loro intersezione è una retta passante per quel punto; uno qualunque dei due piani è diviso dalla comune intersezione in due semipiani situati da parti opposte rispetto all'altro.

c) Se per un punto H di una retta m si conducono ad essa in piani diversi due perpendicolari a e b, ogni altra retta del piano ab passante per H è perpendicolare alla m, e viceversa ogni perpendicolare alla m per H giace nel piano ab. Il piano ab dicesi perpendicolare alla retta m in H; e la retta perpendicolare m al piano ab in H.

d) Per un punto A appartenente o no ad una retta passa un piano ed uno solo perpendicolare ad essa.

e) Teorema delle tre normali: Se una retta m è perpendicolare ad un piano α e dal piede H esce nel piano una retta a perpendicolare ad una retta r di α (passante o no per il piede H), la terza retta r è perpendicolare al piano am delle prime due.

f) Due piani che si intersecano dividono lo spazio in quattro parti (diedri). Seguono le definizioni di diedro convesso, piatto e concavo.

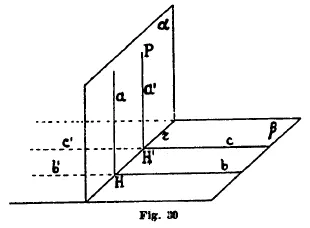
g) Sia β (fig. 30) un piano perpendicolare ad una retta a e sia H il suo piede. Conduciamo per a un piano qualunque α, e sia r la αβ; e conduciamo per H in β la bb' perpendicolare alla r. Per il teorema delle tre normali la b è perpendicolare al piano α e quindi ad a; i due angoli risultano retti. Facendo ruotare il piano ab intorno ad H su se stesso esso rimane perpendicolare alla r e quando la semiretta b va sulla a e la a sulla b', il semipiano β va sul semipiano α ed α su β'. I due diedri e si sovrappongono, sono quindi eguali; il semipiano α biseca dunque il diedro piattoOgni altro semipiano per r è interno all'uno od all'altro dei diedriequindi per una retta r del piano β si può condurre uno ed un solo piano α che bisechi il diedro piattoIl piano α dicesi perpendicolare al piano β; l'angolodicesi sezione normale di ed è retto.

Se per un punto P di α si conduce la perpendicolare a' alla r dal piede e la c in β perpendicolare alla r, anche il piano a'c è perpendicolare alla r; facendo ruotare attorno alla r il semipiano β va in α ed α in β', la semiretta c va sulla a', e la a' sulla c'; dunque= un retto, e quindi a' risulta perpendicolare anche a β e la sezione normaledel diedrorisulta eguale all'altra

h) Retta perpendicolare ad un piano per un punto. Sia H un punto di un piano β (fig. 30), e si conduca per H in β una retta b qualunque, e per H il piano α perpendicolare alla b; sia r la Per H conduciamo nel piano α la perpendicolare a alla r; per il teorema delle tre normali risulta a perpendicolare a β. La unicità della perpendicolare a β per H si dimostra per assurdo.

Se poi il punto dato fosse P esterno al piano β, condotta in β una retta b qualunque e per P il piano α perpendicolare alla b, esso interseca la b e quindi il piano β secondo una retta r. Da P in α si conduca la PH' perpendicolare alla r e per il teorema delle tre normali risulta PH' perpendicolare a β. Per assurdo se ne dimostra subito la unicità.

i) I piani passanti per una retta perpendicolare ad un piano sono perpendicolari ad esso.

k) Se i piani α e β sono tra loro perpendicolari, la perpendicolare PH' alla intersezione abbiamo veduto che è perpendicolare a β. Viceversa, per l'unicità della perpendicolare ad un piano, se due piani α e β sono perpendicolari, e da un punto P di α si conduce la perpendicolare a β essa giace in α.

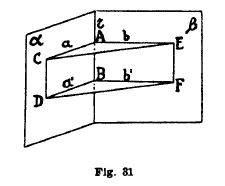
l) Sezione normale di un diedro qualunque. Per due punti A e B (fig. 31) della costola r di un diedro conduciamo nella faccia α le perpendicolari a, a' alla r, e nella faccia β le perpendicolari b, b' alla r. Chiameremo sezioni normali del diedro gli angoliEssi sono eguali. Presi infatti su α AC = BD e su β AE = BF i quadrilateri ACDB, ABFE sono dei rettangoli e quindi CD = AB = EF. La r è perpendicolare ai piani ab ed a'b'; quindi il piano α è perpendicolare ai piani ab ed a'b', la CD che è perpendicolare alla intersezione a dei due piani α ed ab risulta perpendicolare al piano ab e perciò anche alla CE; analogamente risulta perpendicolare alla DF; ed analogamente la EF risulta perpendicolare alle CE ed FD. Inoltre, essendo CD perpendicolare al piano ACE, il piano CDE è perpendicolare al piano ACE, e la EF, perpendicolare anche essa al piano ACE, giace nel piano CDE; perciò il quadrilatero CDEF è un quadrilatero piano cogli angoli retti, ossia è un rettangolo. I triangoli ACE e BDF risultano quindi eguali per il terzo criterio, e gli angoli sono eguali. Le sezioni normali di un diedro qualunque sono dunque eguali.

m) Se due piani α e β sono perpendicolari ad un terzo γ la loro intersezione è perpendicolare a γ.

n) Due piani perpendicolari ad una retta non si incontrano.

o) Definizione di piano assiale di un segmento.

Si dimostra che esso è il luogo geometrico dei punti equidistanti dagli estremi del segmento.

p) Distanza di un punto da un piano; e luogo geometrico dei punti del piano aventi distanza assegnata da un punto esterno.

Corollario: Dato un poligono regolare inscritto in una circonferenza, un punto qualunque della perpendicolare al piano del poligono condotta per il centro è equidistante dai vertici del poligono.

q) Piano bisettore di un diedro e sue proprietà.

Per un punto P del piano γ bisettore del diedro si conduca il piano δ perpendicolare allo spigolo r. I tre piani α, β, γ sono perpendicolari a δ; condotte da P le perpendicolari PH e PK ad α e β esse giacciono in δ; ed unendo il punto M di intersezione della r e di δ con H, P, K, i triangoli rettangoli PHM, PKM sono eguali per avere l'ipotenusa PM in comune e gli angoli eguali perché γ è bisettore di e facendo ruotare attorno alla r, quando γ va su β, α va su γ ed i due angoli si sovrappongono.

Viceversa si dimostra che se un punto P interno ad è equidistante da α e da β, esso appartiene al piano γ bisettore del diedro

r) Definizione di triedro e di angoloide convesso.

s) TEOREMA: In un triedro una faccia è minore della somma delle altre due.

Si dimostra nel solito modo, e si estende all'angoloide.

t) TEOREMA: La somma delle facce di un triedro è minore di quattro retti.

Si dimostra nel solito modo e si estende all'angoloide convesso.

v) Definizione degli angoloidi regolari.

Hanno tutte le facce eguali, ed eguali i diedri formati da due facce consecutive.

x) Definizione di poliedro. Il poliedro si dice regolare quando tutte le facce sono poligoni regolari eguali e gli angoloidi sono regolari eguali.

z) Possono esistere al massimo cinque poliedri regolari, uno con tre, uno con quattro ed uno con cinque facce congruenti in un vertice eguali a dei triangoli equilateri; uno con tre quadrati congruenti in un vertice, ed uno con tre pentagoni regolari congruenti in un vertice.

Questa possibilità si dimostra nel solito modo.

2. Costruzione del tetraedro regolare.

Dimostrata la possibilità dell'esistenza dei cinque poliedri regolari passiamo alla loro effettiva costruzione.

La proprietà del baricentro di un triangolo qualunque si può riconoscere valida anche nella nostra geometria pitagorica indipendentemente dal postulato di Euclide; nel caso del triangolo equilatero è poi facilissimo riconoscere che il baricentro è anche centro delle due circonferenze circoscritta ed inscritta e che il raggio della prima è doppio di quello della seconda.

Per il centro H di un triangolo (fig. 32) equilatero ABC si condurrà la perpendicolare h al piano ABC, e siccome AH è minore di AB si determina nel piano Ah l'intersezione di h con la circonferenza di centro A e raggio AB. Si unisce questo punto D con A, B, C; e si ha DA = DB = DC = AB. Il tetraedro DABC ha per facce quattro triangoli equilateri eguali; gli angoloidi sono dei triedri a facce eguali; ed i diedri sono pure eguali, perché il diedro di spigolo AC ha per sezione normale l'angolo del triangolo isoscele KDB che ha per lato l'altezza della faccia e per base lo spigolo, ed è quindi lo stesso per tutti i diedri. Esiste dunque un tetraedro regolare di dato spigolo AB.

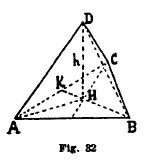
Chiamando l4 lo spigolo, con il teorema di Pitagora si ha:

e quindi

e

Il centro della sfera circoscritta sta sulla h che è il luogo dei punti equidistanti da A, B, C; quindi se D' è l'altro estremo del diametro OD, il piano ADD' è diametrale, il triangolo ADD' è rettangolo perché il punto medio di DD' è equidistante dai vertici, AH è l'altezza di questo triangolo rettangolo e quindi si ha:

Ne segue la regola per la

Inscrizione del tetraedro regolare nella sfera di raggio r.

Preso OD = r e da parte opposta OH =r

si ha in DH l'altezza. Si conduce una circonferenza di diametro DD' = 2r, e per H la perpendicolare al diametro; la sua intersezione con la circonferenza sia il vertice B del tetraedro. Condotto infine il piano passante per HB e perpendicolare al diametro DD', si descrive in esso la circonferenza di raggio HB ed in essa si inscrive il triangolo equilatero ABC. Il tetraedro ABCD è il tetraedro regolare inscritto.

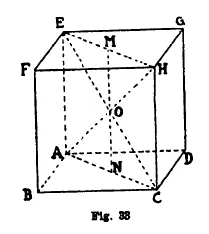
3. Esistenza e costruzione dell'esaedro regolare.

Sia ABCD (fig. 33) un quadrato. Conduciamo per i vertici le perpendicolari al piano del quadrato ABCD da una stessa parte del piano, e prendiamo su esse i segmenti AE, BF, CH, DG eguali al lato AB. I piani EAB, EAD risultano perpendicolari al piano α del quadrato ABCD; e le perpendicolari BF e DG al piano ABCD giacciono rispettivamente nei piani EAB, EAD, dimodoché ABFE e ADGE sono due quadrati eguali al dato. Analogamente la CH coincide con la intersezione dei piani FBC e GDC perpendicolari ad α, e quindi anche FBCH e CDGH sono dei quadrati. Perciò CH è perpendicolare al piano FHG; CD è perpendicolare a CB e CH, quin...

Table of contents

• PREMESSE
• CAPITOLO I - IL TEOREMA DEI DUE RETTI
• CAPITOLO II - IL TEOREMA DI PITAGORA
• CAPITOLO III - IL PENTALFA
• CAPITOLO IV - I POLIEDRI REGOLARI
• CAPITOLO V - IL SIMBOLO DELL'UNIVERSO
• CAPITOLO VI - DIMOSTRAZIONE DEL POSTULATO DI EUCLIDE