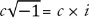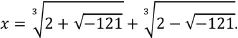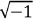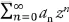Riemann - La geometria dello spazio curvo

Alberto Cogliati, AA.VV., Alberto Cogliati

• Publisher: Pelago
• Year: 2022
• ISBN:
  9791255010371
• Topic: Naturwissenschaften
• Subtopic: Mathematische & Computerphysik

Bernhard Riemann è uno dei fondatori della matematica contemporanea. Portatore di nuove idee nei campi più disparati, dalla geometria, all'analisi, alla teoria dei numeri, è stato uno degli ultimi matematici universali capaci di dominare il sapere del loro tempo con profondità e straordinaria capacità di determinarne gli sviluppi futuri. Il suo approccio, definito concettuale per l'importanza che attribuiva ai concetti anteponendoli a laboriose deduzioni algoritmiche, gli ha permesso di sviluppare teorie di eccezionale portata innovativa. I suoi studi nel campo della geometria differenziale hanno rivoluzionato la concezione stessa dello spazio e fornito, qualche decennio dopo, strumenti indispensabili per la formulazione della teoria della relatività. L'ipotesi di Riemann sulla distribuzione dei numeri primi nell'insieme dei numeri naturali rappresenta ancora oggi una delle sfide che più appassionano i matematici e una sua dimostrazione porterebbe un grande arricchimento delle nostre conoscenze in diversi ambiti della matematica.

FOCUS

L’IMPORTANZA DI RIEMANN

In matematica, è stato scritto, esistono due tipi di scienziati. Da un lato coloro che inaugurano vie lastricate di nuove idee che, per quanto semplici, non sono occorse ad alcuno prima di loro; dall’altro, i matematici che sulle vaste aree rese praticabili dai primi si prodigano a seminare e a raccogliere ricchissime messi. Entrambe le categorie sono indispensabili al progredire della matematica ma solo ai pochi, illustri esponenti della prima schiera è concesso l’onore di scrivere il proprio nome fra i padri della disciplina. Senza dubbio la figura di Bernhard Riemann si colloca tra questi.

L’audacia delle sue vedute, la fecondità dei metodi introdotti e la vastità dei suoi variegati interessi fanno di lui uno dei fondatori della matematica contemporanea.

L’eccezionalità della produzione matematica di Riemann è del resto acuita dalla sua mirabile densità concettuale. Innegabilmente, la breve durata della sua carriera (poco più di un quindicennio) insieme alla difficoltà, più volte lamentata, di dare forma definitiva ai concetti e ai procedimenti che egli si rappresentava nella mente impedirono che la ricchezza del suo pensiero trovasse adeguata espressione nella parola scritta; tuttavia la portata innovativa del suo approccio fu tale che ogni settore del sapere matematico di cui egli si occupò risultò rivoluzionato e profondamente arricchito. Riemann, in grado di dedicarsi con eguale successo alla geometria, all’analisi, alla fisica matematica e alla teoria dei numeri, fu uno degli ultimi matematici universali ai quali fu concesso di dominare il sapere del loro tempo con profondità e straordinaria capacità di determinarne gli sviluppi futuri.

La solidità della figura scientifica di Riemann stride con i tratti di una biografia segnata da ipocondria, salute cagionevole e patologica insicurezza che limitarono fortemente la sua capacità di diffondere le proprie idee al di là di una assai ristretta cerchia di amici e colleghi. Il riconoscimento della fecondità del suo pensiero da parte della comunità matematica fu in buona parte postumo ma nondimeno determinante nel plasmare la forma della matematica odierna.

Al di là dei fondamentali contributi in campi specifici, l’eredità di Riemann consistette anche in un nuovo approccio alla ricerca matematica che segnò una discontinuità rispetto alle precedenti generazioni.

Un nuovo modo di operare che giustamente è stato definito concettuale, per indicare la preponderanza da lui accordata ai concetti rispetto alle laboriose deduzioni algoritmiche che avevano dominato sino ad allora l’opera della maggior parte dei matematici. Per più di una ragione, l’opera di Riemann sembra incarnare il motto di quello che può essere considerato come uno dei suoi maestri, Gustav Lejeune Dirichlet, il quale ebbe a scrivere «prima il pensiero e poi i calcoli».

Una considerazione a parte merita il ruolo delle ricerche di Riemann nel campo della geometria differenziale. Il concetto di varietà in un numero qualunque di dimensioni insieme ad una generalizzazione della nozione classica di curvatura, che era stata propria, sino ad allora, della sola geometria delle superfici, costituì lo strumento tecnico in virtù del quale Einstein poté sviluppare ed enunciare la teoria della relatività generale, ancora oggi alla base della nostra comprensione dell’universo su larga scala.

LE OPERE SCIENTIFICHE

L’ANALISI COMPLESSA

Il primo dei contributi di Riemann risale al dicembre del 1851 quando, a conclusione degli studi all’Università di Gottinga, egli fu chiamato a difendere la propria dissertazione di dottorato. Il titolo, Fondamenti di una teoria generale delle funzioni di una variabile complessa, richiamava gli aspetti fondazionali della trattazione, la quale, come si vedrà, non si limitò ad enunciare nuovi teoremi, ma propose nozioni e procedimenti affatto nuovi i quali segnarono profondamente lo sviluppo della odierna analisi complessa.

Per descrivere i contenuti di questo lavoro conviene procedere un poco a ritroso per ripercorrere la storia dei numeri complessi e accennare agli sviluppi della teoria delle funzioni precedenti ai contributi di Riemann.

Succede di frequente nella storia della matematica che scoperte cruciali si presentino in contesti più complicati rispetto a quelli che oggi ci parrebbe naturale introdurre per descriverle. È questo il caso dei numeri complessi.

Generalmente il primo incontro con queste “esotiche” entità avviene nel contesto della teoria delle equazioni algebriche di secondo grado, cioè equazioni del tipo ax² + bx + c = 0, e più precisamente quando si riconosce che per valori opportuni dei coefficienti reali a, b, c l’equazione non ammette soluzioni reali [cioè numeri reali come soluzioni – ndr] giacché nella formula risolutiva dell’equazione compaiono radici di numeri negativi. Tuttavia, questa circostanza di per sé non conduce in alcun modo alla necessità di introdurre una estensione della nozione di numero reale; infatti essa può essere interpretata semplicemente come una manifestazione del fatto che in tali casi l’equazione non ammette soluzioni (reali).

Tale necessità si manifestò in un altro contesto.

In effetti, l’introduzione di quantità immaginarie, cioè numeri del tipo

, si compì nel corso dei tentativi di risoluzione delle equazioni generali di terzo grado: ax³ + bx² + cx + d = 0, dove a, b, c, d sono numeri assegnati. In un caso particolare, il cosiddetto caso irriducibile, la formula risolutiva di tale equazione (dovuta nel Cinquecento a Niccolò Tartaglia e a Girolamo Cardano) conduce a soluzioni reali che tuttavia sono rappresentate da quantità immaginarie. Un esempio è quello dell’equazione cubica x³ = 15x + 4. Si verifica facilmente che x = 4 è soluzione dell’equazione; tuttavia essa è espressa, in virtù della formula di Cardano, da

Al matematico rinascimentale Raffaele Bombelli va riconosciuto il merito di aver introdotto nel suo trattato Algebra (1572) regole pratiche per il maneggio di queste nuove entità, pur senza porsi il problema di fornirne una definizione precisa. Del resto, per molto tempo il loro stato si mantenne precario, come attestano le varie caratterizzazioni a cui i numeri complessi furono soggetti. Ancora nel 1702, Gottfried Wilhelm Leibniz, ad esempio, arrivò a parlare del numero

addirittura come di «quel mostro dell’analisi, quel portento del mondo ideale, quell’anfibio fra essere e non essere che chiamiamo radice dell’unità negativa».¹

Gradualmente, i matematici si familiarizzarono con i numeri complessi fino ad impiegarli diffusamente nel corso dei loro calcoli e delle loro deduzioni, non solo per affrontare problemi di carattere algebrico, come la soluzione di un’equazione di terzo grado, ma anche in ambito analitico, ad esempio nel calcolo degli integrali definiti di funzioni reali.

Si scoprì che gli strumenti del calcolo differenziale, come la derivata e l’integrale, potevano essere applicati altrettanto proficuamente al campo dei numeri complessi; anzi, l’impiego di quantità immaginarie metteva in luce proprietà e fenomeni assai diversi ed in qualche caso persino più interessanti rispetto a quelli che si presentavano abitualmente nell’ambito della cosiddetta analisi reale.

Una svolta importante si ebbe con la scoperta della rappresentazione geometrica dei numeri complessi ad opera di matematici quali il cartografo danese Caspar Wessel e lo svizzero Jean-Robert Argand, vissuti tra il Settecento e l’Ottocento, che per primi identificarono un numero complesso a + ib con il punto del piano le cui coordinate, rispetto ad un riferimento cartesiano ortogonale, sono date dalla coppia (a, b).

Il grande Carl Friedrich Gauss, pur con qualche tentennamento, si servì implicitamente di tale rappresentazione geometrica nelle varie dimostrazioni da lui fornite del cosiddetto teorema fondamentale dell’algebra (il cui asserto sancisce l’esistenza di n radici complesse di un polinomio di grado n). Egli fu più esplicito in una lettera del 1811 all’amico matematico e astronomo Friedrich Bessel nella quale scriveva: «proprio come pensiamo alla totalità dei numeri reali in termini di una retta infinita, così ci possiamo rappresentare l’insieme di tutte le quantità, reali e immaginarie, per mezzo di un piano infinito nel quale a ogni punto di ascissa = a e ordinata = b corrisponde il numero a + ib».²

La rappresentazione geometrica qui descritta era impiegata dallo stesso Gauss per estendere il concetto di integrale a funzioni di variabile complessa, la quale richiedeva che l’ordinaria nozione di intervallo di integrazione venisse sostituita dalla prescrizione di un particolare cammino di integrazione, cioè da una curva nel piano complesso.

Nella stessa lettera a Bessel, egli informava l’amico circa le proprie ricerche, peraltro mai pubblicate, sull’integrazione di funzioni di variabile complessa. «Che cosa bisogna intendere con ∫ φ(x) dx quando il limite superiore [di integrazione] è a + ib? […] Il passaggio continuo da un valore di x all’altro nel piano complesso ha luogo lungo una curva ed è perciò possibile lungo molti cammini. Affermo ora che l’integrale ∫ φ(x) dx ha un unico valore anche se preso lungo cammini diversi purché φ(x) sia a un sol valore e non diventi infinita nello spazio compreso fra due cammini. Questo è un teorema molto bello».³

Il teorema cui Gauss faceva cenno, oggi noto come teorema integrale di Cauchy, fu uno dei risultati principali delle numerose indagini che impegnarono il matematico francese Augustin-Louis Cauchy per quasi un quarantennio. A lui si devono i primi enunciati e le prime dimostrazioni di risultati cruciali in analisi complessa: oltre al già citato teorema integrale, l’individuazione di equazioni (oggi dette di Cauchy-Riemann) che garantiscono, in buona sostanza, notevoli proprietà di regolarità tra le quali l’infinita derivabilità e la possibilità di espandere in serie di potenze (cioè espressioni del tipo

) una qualunque funzione di variabile complessa, z → f(z) che vi soddisfi.

Era questo lo stato di avanzamento della disciplina quando, nel novembre del 1851, Riemann presentò all’università di Gottinga la sua tesi di dottorato sui fondamenti della teoria delle funzioni di una variabile complessa.

Inizialmente orientato verso studi di teologia e filologia, nel 1846, all’età di diciannove anni, Riemann si era iscritto all’Università di Gotti...