eBook - ePub
Infinite Powers
The Story of Calculus - The Language of the Universe
Steven Strogatz
This is a test
Share book
- English
- ePUB (mobile friendly)
- Available on iOS & Android
eBook - ePub
Infinite Powers
The Story of Calculus - The Language of the Universe
Steven Strogatz
Book details
Book preview
Table of contents
Citations
About This Book
Shortlisted for the Royal Society Science Book Prize 2019 A magisterial history of calculus (and the people behind it) from one of the world's foremost mathematicians. This is the captivating story of mathematics' greatest ever idea: calculus. Without it, there would be no computers, no microwave ovens, no GPS, and no space travel. But before it gave modern man almost infinite powers, calculus was behind centuries of controversy, competition, and even death. Taking us on a thrilling journey through three millennia, professor Steven Strogatz charts the development of this seminal achievement from the days of Archimedes to today's breakthroughs in chaos theory and artificial intelligence. Filled with idiosyncratic characters from Pythagoras to Fourier, Infinite Powers is a compelling human drama that reveals the legacy of calculus on nearly every aspect of modern civilisation, including science, politics, medicine, philosophy, and much besides.
Frequently asked questions
How do I cancel my subscription?
Can/how do I download books?
At the moment all of our mobile-responsive ePub books are available to download via the app. Most of our PDFs are also available to download and we're working on making the final remaining ones downloadable now. Learn more here.
What is the difference between the pricing plans?
Both plans give you full access to the library and all of Perlego’s features. The only differences are the price and subscription period: With the annual plan you’ll save around 30% compared to 12 months on the monthly plan.
What is Perlego?
We are an online textbook subscription service, where you can get access to an entire online library for less than the price of a single book per month. With over 1 million books across 1000+ topics, we’ve got you covered! Learn more here.
Do you support text-to-speech?
Look out for the read-aloud symbol on your next book to see if you can listen to it. The read-aloud tool reads text aloud for you, highlighting the text as it is being read. You can pause it, speed it up and slow it down. Learn more here.
Is Infinite Powers an online PDF/ePUB?
Yes, you can access Infinite Powers by Steven Strogatz in PDF and/or ePUB format, as well as other popular books in Mathématiques & Algèbre. We have over one million books available in our catalogue for you to explore.
Information
Topic
MathématiquesSubtopic
Algèbre
THE BEGINNINGS OF mathematics were grounded in everyday concerns. Shepherds needed to keep track of their flocks. Farmers needed to weigh the grain reaped in the harvest. Tax collectors had to decide how many cows or chickens each peasant owed the king. Out of such practical demands came the invention of numbers. At first they were tallied on fingers and toes. Later they were scratched on animal bones. As their representation evolved from scratches to symbols, numbers facilitated everything from taxation and trade to accounting and census taking. We see evidence of all this in Meso-potamian clay tablets written more than five thousand years ago: row after row of entries recorded with the wedge-shaped symbols called cuneiform.
Along with numbers, shapes mattered too. In ancient Egypt, the measurement of lines and angles was of paramount importance. Each year surveyors had to redraw the boundaries of farmers’ fields after the summer flooding of the Nile washed the borderlines away. That activity later gave its name to the study of shape in general: geometry, from the Greek gē, “earth,” and metrēs, “measurer.”
At the start, geometry was hard-edged and sharp-cornered. Its predilection for straight lines, planes, and angles reflected its utilitarian origins — triangles were useful as ramps, pyramids as monuments and tombs, and rectangles as tabletops, altars, and plots of land. Builders and carpenters used right angles for plumb lines. For sailors, architects, and priests, knowledge of straight-line geometry was essential for surveying, navigating, keeping the calendar, predicting eclipses, and erecting temples and shrines.
Yet even when geometry was fixated on straightness, one curve always stood out, the most perfect of all: the circle. We see circles in tree rings, in the ripples on a pond, in the shape of the sun and the moon. Circles surround us in nature. And as we gaze at circles, they gaze back at us, literally. There they are in the eyes of our loved ones, in the circular outlines of their pupils and irises. Circles span the practical and the emotional, as wheels and wedding rings, and they are mystical too. Their eternal return suggests the cycle of the seasons, reincarnation, eternal life, and never-ending love. No wonder circles have commanded attention for as long as humanity has studied shapes.
Mathematically, circles embody change without change. A point moving around the circumference of a circle changes direction without ever changing its distance from a center. It’s a minimal form of change, a way to change and curve in the slightest way possible. And, of course, circles are symmetrical. If you rotate a circle about its center, it looks unchanged. That rotational symmetry may be why circles are so ubiquitous. Whenever some aspect of nature doesn’t care about direction, circles are bound to appear. Consider what happens when a raindrop hits a puddle: tiny ripples expand outward from the point of impact. Because they spread equally fast in all directions and because they started at a single point, the ripples have to be circles. Symmetry demands it.
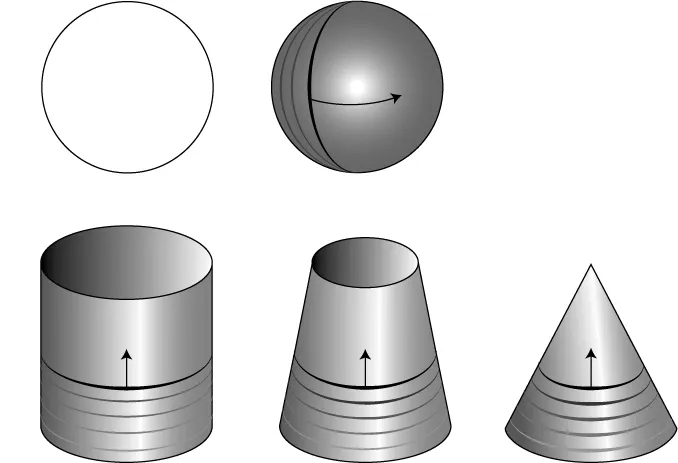
Circles can also give birth to other curved shapes. If we imagine skewering a circle on its diameter and spinning it around that axis in three-dimensional space, the rotating circle makes a sphere, the shape of a globe or a ball. When a circle is moved vertically into the third dimension along a straight line at right angles to its plane, it makes a cylinder, the shape of a can or a hatbox. If it shrinks at the same time as it’s moving vertically, it makes a cone; if it expands as it moves vertically, it makes a truncated cone (the shape of a lampshade).
Circles, spheres, cylinders, and cones fascinated the early geometers, but they found them much harder to analyze than triangles, rectangles, squares, cubes, and other rectilinear shapes made of straight lines and flat planes. They wondered about the areas of curved surfaces and the volumes of curved solids but had no clue how to solve such problems. Roundness defeated them.
Infinity as a Bridge Builder
Calculus began as an outgrowth of geometry. Back around 250 BCE in ancient Greece, it was a hot little mathematical startup devoted to the mystery of curves. The ambitious plan of its devotees was to use infinity to build a bridge between the curved and the straight. The hope was that once that link was established, the methods and techniques of straight-line geometry could be shuttled across the bridge and brought to bear on the mystery of curves. With infinity’s help, all the old problems could be solved. At least, that was the pitch.
At the time, that plan must have seemed pretty far-fetched. Infinity had a dubious reputation. It was known for being scary, not useful. Worse yet, it was nebulous and bewildering. What was it exactly? A number? A place? A concept?
Nevertheless, as we’ll see soon and in the chapters to come, infinity turned out to be a godsend. Given all the discoveries and technologies that ultimately flowed from calculus, the idea of using infinity to solve difficult geometry problems has to rank as one of the best ideas anyone ever had.
Of course, none of that could have been foreseen in 250 BCE. Still, infinity did put some impressive notches in its belt right away. One of its first and finest was the solution of a long-standing enigma: how to find the area of a circle.
A Pizza Proof
Before I go into the details, let me sketch the argument. The strategy is to reimagine the circle as a pizza. Then we’ll slice that pizza into infinitely many pieces and magically rearrange them to make a rectangle. That will give us the answer we’re looking for, since moving slices around obviously doesn’t change their area from what they were originally, and we know how to find the area of a rectangle: we just multiply its width times its height. The result is a formula for the area of a circle.
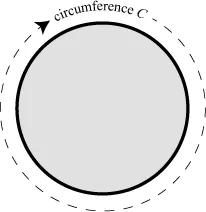
For the sake of this argument, the pizza needs to be an idealized mathematical pizza, perfectly flat and round, with an infinitesimally thin crust. Its circumference, abbreviated by the letter C, is the distance around the pizza, measured by tracing around the crust. Circumference isn’t something that pizza lovers ordinarily care about, but if we wanted to, we could measure C with a tape measure.
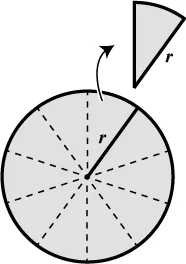
Another quantity of interest is the pizza’s radius, r, defined as the distance from its center to every point on its crust. In particular, r also measures how long the straight side of a slice is, assuming that all the slices are equal and cut from the center out to the crust.
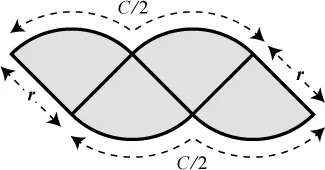
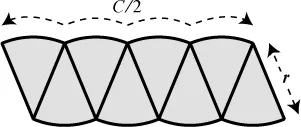
Suppose we start by dividing the pie into four quarters. Here’s one way to rearrange them, but it doesn’t look too promising.
The new shape looks bulbous and strange with its scalloped top and bottom. It’s certainly not a rectangle, so its area is not easy to guess. We seem to be going backward. But as in any drama, the hero needs to get into trouble before triumphing. The dramatic tension is building.
While we’re stuck here, though, we should notice two things, because they are going to hold true throughout the proof, and they will ultimately give us the dimensions of the rectangle we’re seeking. The first observation is that half of the crust became the curvy top of the new shape, and the other half became the bottom. So the curvy top has a length equal to half the circumference, C/2, and so does the bottom, as shown in the diagram. That length is eventually going to turn into the long side of the rectangle, as we’ll see. The other thing to notice is that the tilted straight sides of the bulbous shape are just the sides of the original pizza slices, so they still have length r. That length is eventually going to turn into the short side of the rectangle.
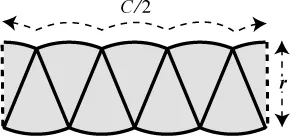
The reason we aren’t seeing any signs of the desired rectangle yet is that we haven’t cut enough slices. If we make eight slices and rearrange them like so, our picture starts to look more nearly rectangular.
In fact, the pizza starts to look like a parallelogram. Not bad — at least it’s almost rectilinear. And the scallops on the top and bottom are a lot less bulbous than they were. They flattened out when we used more slices. As before, they have curvy length C/2 on the top and bottom and a slanted-side length r.
To spruce up the picture even more, suppose we cut one of the slanted end pieces in half lengthwise and shift that half to the other side.
Now the shape looks very much like a rectangle. Admittedly, it’s still not perfect because of the scalloped top and bottom caused by the curvature of the crust, but at least we’re making progress.
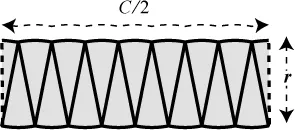
Since making more pieces seems to be helping, let’s keep slicing. With sixteen slices and the cosmetic sprucing-up of the end piece, as we did before, we get this result:
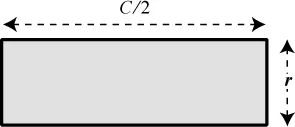
The more slices we take, the more we flatten out the scallops produced by the crust. Our maneuvers are producing a sequence of shapes that are magically homing in on a certain rectangle. Because the shapes keep getting closer and closer to that rectangle, we’ll call it the limiting rectangle.
The point of all this is that we can easily find the area of this limiting rectangle by multiplying its width by its height. All that remains is to find that height and width in terms of the circle’s dimensions. Well, since the slices are standing upright, the height is just the radius r of the original circle. And the width is half the circumference of the circle; that’s because half of the circumference (the crust of the pizza) went into making the top of the rectangle and the other half got used on the bottom, just as it did at every intermediate stage of working with the bulbous shapes. Thus the width is half the circumference, C/2. Putting everything together, the area of the limiting rectangle is given by its height times its width, namely, A = r × C/2 = rC/2. And since moving the pizza slices around did not change their area, this must also be the area of the original circle!
This result for the area of a circle, A = rC/2, was first proved (using a similar but much more careful argument) by the ancient Greek mathematician Archimedes (287–212 BCE) in his essay “Measurement of a Circle.”
The most innovative aspect of the proof is the way infinity came to the rescue. When we had only four slices, or eight, or sixteen, the best we could do was rearrange the pizza into an imperfect scalloped shape. After an unpromising start, the more slices we took, the more rectangular the shape became. But it was only in the limit of infinitely many slices that it became truly rectangular. That’s the big idea behind calculus. Everything becomes simpler at infinity.
Limits and the Riddle of the Wall
A limit is like an unattainable goal. You can get closer and closer to it, but you can never get all the way there.
For example, in the pizza proof we were able to make the scalloped shapes more and more nearly rectangular by cutting enough slices and rearranging them. But we could never make them genuinely rectangular. We could only approach that state of perfection. Fortunately, in calculus, the unattainability of the limit usually doesn’t matter. We can often solve the problems we’re working on by fantasizing that we can actually reach the limit and then seeing what that fantasy implies. In fact, many of the greatest pioneers of the subject did precisely that and made great discoveries by doing so. Logical, no. Imaginative, yes. Successful, very.
A limit is a subtle concept but a central one in calculus. It’s elusive because it’s not a common idea in daily life. Perhaps the closest analogy is the Riddle of the Wall. If you walk halfway to the wall, and then you walk half the remaining distance, and then you walk half of that, and on and on, will there ever be a step when you finally get to the wall?
The answer is clearly no, because the Riddle of the Wall stipulates that at each step,...