Beautiful Geometry

Eli Maor, Eugen Jost

• Publisher: Princeton University Press
• Year: 2014
• ISBN:
  9781400848331
• Topic: Mathematik
• Subtopic: Geometrie

An exquisite visual celebration of the 2, 500-year history of geometry If you've ever thought that mathematics and art don't mix, this stunning visual history of geometry will change your mind. As much a work of art as a book about mathematics, Beautiful Geometry presents more than sixty exquisite color plates illustrating a wide range of geometric patterns and theorems, accompanied by brief accounts of the fascinating history and people behind each. With artwork by Swiss artist Eugen Jost and text by math historian Eli Maor, this unique celebration of geometry covers numerous subjects, from straightedge-and-compass constructions to intriguing configurations involving infinity. The result is a delightful and informative illustrated tour through the 2, 500-year-old history of one of the most important branches of mathematics.

Plate 1. Sunrise over Miletus

 

1

Thales of Miletus

Thales (ca. 624–546 BCE) was the first of the long line of mathematicians of ancient Greece that would continue for nearly a thousand years. As with most of the early Greek sages, we know very little about his life; what we do know was written several centuries after he died, making it difficult to distinguish fact from fiction. He was born in the town of Miletus, on the west coast of Asia Minor (modern Turkey). At a young age he toured the countries of the Eastern Mediterranean, spending several years in Egypt and absorbing all that their priests could teach him.

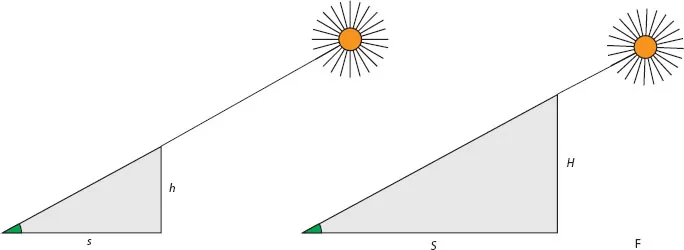
While in Egypt, Thales calculated the height of the Great Cheops pyramid, a feat that must have left a deep impression on the locals. He did this by planting a staff into the ground and comparing the length of its shadow to that cast by the pyramid. Thales knew that the pyramid, the staff, and their shadows form two similar right triangles. Let us denote by H and h the heights of the pyramid and the staff, respectively, and by S and s the lengths of their shadows (see figure 1.1). We then have the simple equation H/S = h/s, allowing Thales to find the value of H from the known values of S, s, and h. This feat so impressed Thales’s fellow citizens back home that they recognized him as one of the Seven Wise Men of Greece.

Mathematics was already quite advanced during Thales’s time, but it was entirely a practical science, aimed at devising formulas for solving a host of financial, commercial, and engineering problems. Thales was the first to ask not only how a particular problem can be solved, but why. Not willing to accept facts at face value, he attempted to prove them from fundamental principles. For example, he is credited with demonstrating that the two base angles of an isosceles triangle are equal, as are the two vertical angles formed by a pair of intersecting lines. He also showed that the diameter of a circle cuts it into two equal parts, perhaps by folding over the two halves and observing that they exactly overlapped. His proofs may not stand up to modern standards, but they were a first step toward the kind of deductive mathematics in which the Greeks would excel.

Thales’s most famous discovery, still named after him, says that from any point on the circumference of a circle, the diameter always subtends a right angle. This was perhaps the first known invariance theorem—the fact that in a geometric configuration, some quantities remain the same even as others are changing. Many more invariance theorems would be discovered in the centuries after Thales; we will meet some of them in the following chapters.

Figure 1.1

Thales’s theorem can actually be generalized to any chord, not just the diameter. Such a chord divides the circle into two unequal arcs. Any point lying on the larger of these arcs subtends the chord at a constant angle α < 90°; any point on the smaller arc subtends it at an angle β = 180° – α > 90°.¹ Plate 1, Sunrise over Miletus, shows this in vivid color.

NOTE:

1. The converse of Thales’s theorem is also true: the locus of all points from which a given line segment subtends a constant angle is an arc of a circle having the line segment as chord. In particular, if the angle is 90°, the locus is a full circle with the chord as diameter.

2

Triangles of Equal Area

Around 300 BCE, Euclid of Alexandria wrote his Elements, a compilation of the state of mathematics as it was known at his time. Written in 13 parts (“books”) and arranged in strict logical order of definitions, postulates (today we call them axioms), and propositions (theorems), it established mathematics as a deductive discipline, in which every theorem must be proved based on previously established theorems, until we fall back on a small set of postulates whose validity we assume to be true from the outset. Euclid’s 23 opening definitions, 10 axioms, and 465 theorems cover all of classical (“Euclidean”) geometry—the geometry we learn in school—as well as elementary number theory. The Elements is considered the most influential book in the history of mathematics. It has had an enormous influence on generations of mathematicians, scientists, and philosophers, and its terse style and rigid structure of definitions, postulates, propositions, and demonstrations (proofs) became the paradigm of how mathematics should be done.

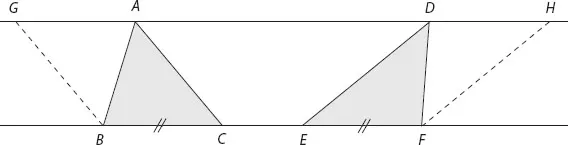
Proposition 38 of Book I of the Elements says, Triangles which are on equal bases and in the same parallels are equal to one another. In modern language this reads: all triangles with the same base and top vertices that lie on a line parallel to the base have the same area.

In proving this theorem, it would be tempting to use the familiar formula for the area of a triangle, A = bh/2, and argue that since two triangles with the same base b and top vertices that lie on a line parallel to the base also have the same height h, they must have the same area. This “algebraic” proof, however, would not satisfy Euclid; he insisted that a proof should be based strictly on geometric considerations. Here is how he proved it:

In figure 2.1, let triangles ABC and DEF have equal bases BC and EF. Their vertices A and D are on a line parallel to BC and EF. We extend AD to points G and H, where GB is parallel to AC and HF is parallel to DE. Then the figures GBCA and DEFH are parallelograms with the same area, for they have equal bases BC and EF and lie between the same parallels BF and GH. Now the area of triangle ABC is half the area of parallelogram GBCA, and the area of triangle DEF is half the area of parallelogram DEFH. Therefore the two triangles have the same area—QED.¹

 

Plate 2. Triangles of Equal Area

 

Figure 2.1

Our illustration (plate 2) shows three identical red triangles, each of whose sides can be regarded as a base. A series of blue triangles are built on each base, with their vertices moving along a line parallel to that base. They get narrower as the vertices move farther out, yet they all have exactly the same area, providing another example of a quantity that remains unchanged even as other quantities in the configuration vary.

This theorem may seem rather unassuming, but Euclid makes good use of it in proving other, more advanced theorems; most famous among them is the Pythagorean theorem, to which we will turn in chapters 5 and 6.

NOTE:

1. QED stands for quod erat demonstrandum, Latin for “that which was to be demonstrated.”

3

Quadrilaterals

Here is a little-known jewel of a theorem that never fails to amaze me: take any quadrilateral (four-sided polygon), connect the midpoints of adjacent sides, and—surprise—you’ll get a parallelogram! The surprise lies in the word any. No matter how skewed your quadrilateral is, the outcome will always be a parallelogram. The theorem holds true even for the dart-shaped quadrilateral shown in the top-left corner of plate 3. And that’s not all: the area of the parallelogram will ...