Einstein's Apple: Homogeneous Einstein Fields

Homogeneous Einstein Fields

Engelbert L Schucking, Eugene J Surowitz

• Publisher: WSPC
• Year: 2015
• eBook ISBN: 9789814630092
• Topic: Biological Sciences
• Subtopic: Science General
• Index: Biological Sciences

We lift a veil of obscurity from a branch of mathematical physics in a straightforward manner that can be understood by motivated and prepared undergraduate students as well as graduate students specializing in relativity. Our book on "Einstein Fields" clarifies Einstein's very first principle of equivalence (1907) that is the basis of his theory of gravitation. This requires the exploration of homogeneous Riemannian manifolds, a program that was suggested by Elie Cartan in "Riemannian Geometry in an Orthogonal Frame," a 2001 World Scientific publication.

Einstein's first principle of equivalence, the key to his General Relativity, interprets homogeneous fields of acceleration as gravitational fields. The general theory of these "Einstein Fields" is given for the first time in our monograph and has never been treated in such exhaustive detail. This study has yielded significant new insights to Einstein's theory. The volume is heavily illustrated and is accessible to well-prepared undergraduate and graduate students as well as the professional physics community.

Contents:

• "The Happiest Thought of My Life"
• Accelerated Frames
• Torsion and Telemotion
• Inertial and Gravitational Fields in Minkowski Spacetime
• The Notion of Torsion
• Homogeneous Fields on Two-dimensional Riemannian Manifolds
• Homogeneous Vector Fields in N-dimensions
• Homogeneous Fields on Three-dimensional Spacetimes: Elementary Cases
• Proper Lorentz Transformations
• Limits of Spacetimes
• Homogeneous Fields in Minkowski Spacetimes
• Euclidean Three-dimensional Spaces
• Homogeneous Fields in Arbitrary Dimension
• Summary

Readership: Physics graduates, physicists, mathematicians, people interested in Einstein.
Key Features:

• An introduction to the use of mathematical torsion and teleparallelism for general relativity
• Elie Cartan's suggestions to an uncomprehending Einstein were initially overlooked but later used by him to explore possibilities for unified field theories
• Our presentation provides an introduction to torsion and its relation to gravitation considered too esoteric for most textbooks

CHAPTER 1

ACCELERATED FRAMES

A.Born Motion

Born’s motion stands in analogy to an observer’s motion on the circle

of radius ρ in the (x-y)-plane. If the motion is at constant speed along the circle, an observer experiences a constant acceleration in the direction opposite from the center of motion. In Born motion, we require an observer to feel constant acceleration in Minkowski spacetime.

We introduce into the (x-t)-plane (with c = 1) “Born-polar” coordinates

and they yield the line element in the form

since the differentials of equations (1.A.2) are related by

The vector form of the line element is

where the vector fields

are orthonormal. The coordinate lines ρ = constant are the hyperbolae

of Born motion. Its time-like worldlines, with proper time s as parameter,

have the unit tangent vector

The acceleration vector is given by

with the aid of (1.A.4). This shows that 1/ρ is the magnitude of the acceleration and the hyperbolae (1.A.7) are the worldlines of constant acceleration.

For Born motion, acceleration becomes the analog of the curvature of circular motion and the hyperbolic functions replace the trigonometric ones of circular motion.

It is easy to construct a picture of the vector fields e₀ and e₁ of (1.A.3) that show, in a region of Minkowski spacetime, the local four-velocity and four acceleration. [See Figure 1.A.1.]

It is clear that the frame field is invariant under motions in the new time coordinate τ but not under motions in the ρ-direction because the size of the acceleration is 1/ρ.

Here was a problem that Einstein apparently had not noticed in his 1907 paper on the equivalence principle. In Newton’s theory the acceleration, γ, could be a vector in the x-direction, constant in space and time, independent of the velocity of a body moving in the x-direction. Not so in Minkowski spacetime. There the acceleration vector has to be orthogonal to the 4-velocity; it would appear that homogeneity of the acceleration field in spacetime could no longer be achieved.

Figure 1.A.1 Born Motion Vectors

Apparently Max Planck had noticed the problem. It was four months after Einstein had mailed his paper that he sent a correction to the Jahrbuch. It began:

“A letter by Mr. Planck induced me to add the following supplementary remark so as to prevent a misunderstanding that could arise easily: In the section ‘Principle of relativity and gravitation’, a reference system at rest situated in a temporally constant, homogeneous gravitational field is treated as physically equivalent to a uniformly accelerated, gravitation-free reference system. The concept ‘uniformly accelerated’ needs further clarification.” [Einstein, 1908]

Einstein then pointed out that the equivalence was to be restricted to a body with zero velocity in the accelerated system. In a linear approximation, he concluded, this was sufficient because only linear terms had to be taken into account.

Ei...

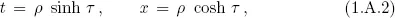
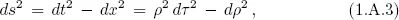
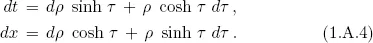
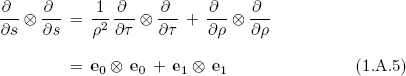
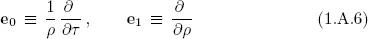
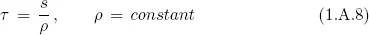
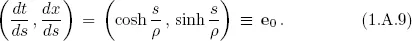
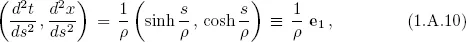
Table of contents

• Cover Page
• Title
• Copyright
• Dedication
• Preface
• Table of Contents
• List of Figures
• 0. “The Happiest Thought of My Life”
• 1. Accelerated Frames
• 2. Torsion and Telemotion
• 3. Inertial and Gravitational Fields in Minkowski Spacetime
• 4. The Notion of Torsion
• 5. Homogeneous Fields on Two-dimensional Riemannian Manifolds
• 6. Homogeneous Vector Fields in N-dimensions
• 7. Homogeneous Fields on Three-dimensional Spacetimes: Elementary Cases
• 8. Proper Lorentz Transformations
• 9. Limits of Spacetimes
• 10. Homogeneous Fields in Minkowski Spacetimes
• 11. Euclidean Three-dimensional Spaces
• 12. Homogeneous Fields in Arbitrary Dimension
• 13. Summary
• Appendix A. Basic Concepts
• Appendix B. A Non-trivial Global Frame Bundle
• Appendix C. Geodesics of the Poincaré Half-Plane
• Appendix D. Determination of Homogeneous Fields in Two-dimensional Riemannian Spaces
• Appendix E. Space Expansion
• Appendix F. The Reissner-Nordstrom Isotropic Field
• Appendix G. The Cremona Transformation
• Appendix H. Hessenberg’s “Vectorial Foundation of Differential Geometry”
• Appendix K. Gravitation Is Torsion
• Appendix R. References
• Appendix X. Index
• Appendix N. Notations and Conventions