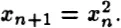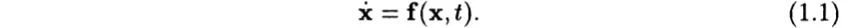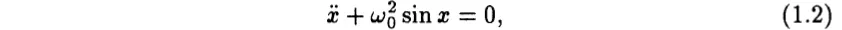Chaotic Dynamics of Nonlinear Systems

S. Neil Rasband

• Editorial: Dover Publications
• Año: 2015
• ISBN:
  9780486805771
• Categoría: Ciencias físicas
• Categoría: Comportamiento caótico en los sistemas

Written when the young science of chaos was gaining a foothold in the scientific community, this book introduces the field's concepts, applications, theory, and technique. Suitable for advanced undergraduates and graduate students, researchers, and teachers of mathematics, physics, and engineering, the text's major prerequisite is familiarity with differential equations and linear vector spaces.
Author S. Neil Rasband discusses the major models for the transitions to chaos exhibited by dynamic systems, introducing the `classical` topics and examples fundamental to the discipline. The most important routes to chaos are presented within a unified framework and supported by integrated problem sets. Topics include one- and two-dimensional maps, universality theory, fractal dimension, differential and conservative dynamics, and other subjects. The text is supplemented by a helpful glossary, references, and an index.

CHAPTER ONE

INTRODUCTION

There are more things in heaven and earth, Horatio, than are dreamt of in your philosophy.

(W. Shakespeare, Hamlet, Act I, Scene 5)

Arguably the most broad based revolution in the worldview of science in the twentieth century will be associated with chaotic dynamics. Yes, I know about Quantum Mechanics and Relativity, and for physicists and philosophers these theories must rank above Chaos for their impact on the way we view the world. My assertion, however, refers to science in general, not just to physics. Leaving improved diagnostic instrumentation aside, it is not clear that Quantum Mechanics or Relativity have had any appreciable effect whatever on medicine, biology, or geology. Yet chaotic dynamics is having an important impact in all of these fields, as well as many others, including chemistry and physics.

Surely part of the reason for this broad application is that chaotic dynamics is not something that is part of a specific physical model, limited in its application to one small area of science. But rather chaotic dynamics is a consequence of mathematics itself and hence appears in a broad range of physical systems. Thus, although the mathematical representations of these physical systems can be very different, they often share common properties. In this introductory chapter we outline in a qualitative way some of the common features of chaos and introduce the reader to some chaotic phenomena. We further introduce some of the methods employed in the study of chaotic dynamics. Precision is left to discussions in subsequent chapters.

1.1 Chaos and Nonlinearity

The very use of the word “chaos” implies some observation of a system, perhaps through some measurement, and that these observations or measurements vary unpredictably. We often say observations are chaotic when there is no discernable regularity or order. We may refer to spatial patterns as chaotic if they appear to have less symmetry than other, more ordered states. In more technical terms we would say that the correlation in observations separated by either space or time appears to be limited. However, from the outset we must make clear that we are not speaking of the observation of random events, such as the flipping of a coin. Chaotic dynamics refers to deterministic development with chaotic outcome. Another way to say this is that from moment to moment the system is evolving in a deterministic way, i.e., the current state of a system depends on the previous state in a rigidly determined way. This is in contrast to a random system where the present observation has no causal connection to the previous one. The outcome of one coin toss does not depend in any way on the previous one. A system exhibiting chaotic dynamics evolves in a deterministic way, but measurements made on the system do not allow the prediction of the state of the system even moderately far into the future.

Whenever dynamical chaos is found, it is accompanied by nonlinearity. Nonlinearity in a system simply means that the measured values of the properties of a system in a later state depend in a complicated way on the measured values in an earlier state. By complicated we mean something other than just proportional to, differing by a constant, or some combination of these two. Although by these remarks, we do not mean to imply that somewhat complicated phenomena cannot be modeled by linear relations.

A simple, nonlinear, mathematical example would be for the observable x in the (n + l)th state to depend on the square of the observable x in the nth state, i.e.,

Such relations are termed mappings, and this is a simple example of a nonlinear map of the nth state to the (n + l)th state. A familiar physical example would be the temperature from one moment to the next as water is brought to a boil. At the end of this process the temperature in the (n + l)th state is just equal to the temperature in the nth state, but this is clearly not true as the water is being heated to its boiling temperature. Frequently the problem of modeling real-world systems with mathematical equations begins with a linear model. But when finer details or more accurate results are desired, additional nonlinear terms must be added.

Naturally, an uncountable variety of nonlinear relations is possible, depending perhaps on a multitude of parameters. These nonlinear relations are frequently encountered in the form of difference equations, mappings, differential equations, partial differential equations, integral equations, or even sometimes combinations of these. As we look deeper into specific causes of chaos, we shall see that chaos is not possible without nonlinearity. Nonlinear relations are not sufficient for chaos, but some form of nonlinearity is necessary for chaotic dynamics.

Having considered briefly nonlinear mappings, we now consider somewhat more closely systems modeled by differential equations. It is convenient when discussing the properties of differential equations to write them in a standard, first-order form:

If the f in (1.1) is independent of t, then the equation is said to be autonomous; otherwise it is nonautonomous. For such a system to be chaotic it must have than one degree of freedom, or be nonautonomous. We illustrate this with the familiar example of a simple pendulum. The differential equation for a simple pendulum is often written in the form

where x represents the angular displacement of the pendulum from the vertical position, two overdots denote two derivatives with respect to time in the usual way, and ω₀ denotes the natural frequency of the pendulum for small angular displacements. Even though this system is highly nonlinear, it does not exhibit chaotic dynamics. There is only the single degree of freedom associated with x and the right-hand side is the constant zero. If, instead, we replaced the zero in (1.2) with some function f(x, t), then the system becomes nonautonomous and may exhibit chaotic dynamics, depending of course, on the exact nature of the function f(x, t). ...