Foundations and Fundamental Concepts of Mathematics

Howard Eves

• Editorial: Dover Publications
• Año: 2012
• ISBN:
  9780486132204
• Categoría: Mathematics
• Categoría: Logic in Mathematics

This third edition of a popular, well-received text offers undergraduates an opportunity to obtain an overview of the historical roots and the evolution of several areas of mathematics.
The selection of topics conveys not only their role in this historical development of mathematics but also their value as bases for understanding the changing nature of mathematics. Among the topics covered in this wide-ranging text are: mathematics before Euclid, Euclid's Elements, non-Euclidean geometry, algebraic structure, formal axiomatics, the real numbers system, sets, logic and philosophy and more. The emphasis on axiomatic procedures provides important background for studying and applying more advanced topics, while the inclusion of the historical roots of both algebra and geometry provides essential information for prospective teachers of school mathematics.
The readable style and sets of challenging exercises from the popular earlier editions have been continued and extended in the present edition, making this a very welcome and useful version of a classic treatment of the foundations of mathematics. `A truly satisfying book.` — Dr. Bruce E. Meserve, Professor Emeritus, University of Vermont.

1

MATHEMATICS BEFORE EUCLID

1.1 The Empirical Nature of Pre-Hellenic Mathematics

The thesis can be advanced that mathematics arose from necessity. The annual inundation of the Nile Valley, for example, forced the Egyptians to develop some system for redetermining land markings; in fact, the word geometry means “measurement of the earth.” The need for mensuration formulas was especially imperative if, as Herodotus remarked, taxes in Egypt were paid on the basis of land area. The Babylonians likewise encountered an urgent need for mathematics in the construction of the great engineering structures for which they were famous. Marsh drainage, irrigation, and flood control made it possible to convert the land along the Tigris and Euphrates rivers into a rich agricultural region. Similar undertakings undoubtedly occurred in early times in south-central Asia along the Indus and Ganges rivers, and in eastern Asia along the Hwang Ho and the Yangtze. The engineering, financing, and administration of such projects required the development of considerable technical knowledge and its attendant mathematics. A useable calendar had to be computed to serve agricultural needs, and this required some basic astronomy with its concomitant mathematics. Again, the demand for some system of uniformity in barter was present in even the earliest civilizations; this fact also furnished a pronounced stimulus to mathematical development. Finally, early religious ritual found need for some basic mathematics.¹

Thus there is a basis for saying that mathematics, beyond that implied by primitive counting, originated during the period of the fifth, fourth, and third millennia B.C. in certain areas of the ancient orient as a practical science to assist in engineering, agricultural, and business pursuits and in religious ritual. Although the initial emphasis was on mensuration and practical arithmetic, it was natural that a special craft should come into being for the application, instruction, and development of the science and that, in turn, tendencies toward abstraction should then assert themselves and the subject be studied, to some extent, for its own sake. In this way a basis for the beginnings of theoretical geometry grew out of mensuration, and the first traces of elementary algebra evolved from practical arithmetic.²

In our study of early mathematics we are restricted essentially to that of Egypt and Babylonia. The ancient Egyptians recorded their work on stone and papyrus, the latter fortunately enduring because of Egypt’s unusually dry climate; the Babylonians used imperishable baked clay tablets. In contrast to the use of these media, the early Indians and Chinese used very perishable writing materials like bark and bamboo. Thus it has come to pass that we have a fair quantity of definite information, obtained from primary sources, about the science and the mathematics of ancient Egypt and Babylonia, while we know very little indeed, with any degree of certainty, about these fields of study in ancient India and China.

It is the nature, rather than the content, of this pre-Hellenic mathematics that concerns us here, and in this regard it is important to note that, outside of very simple considerations, the mathematical relations employed by the Egyptians and by the Babylonians resulted essentially from “trial and error” methods. In other words, to a great extent the earliest mathematics was little more than a practically workable empiricism—a collection of rule-of-thumb procedures that gave results of sufficient acceptability for the simple needs of those early civilizations. Thus the Egyptian and Babylonian formulas for volumes of granaries and areas of land were arrived at by trial and error, with the result that many of these formulas are definitely faulty. For example, an Egyptian formula for finding the area of a circle was to take the square of eight ninths of the circle’s diameter. This is not correct, as it is equivalent to taking π = (4/3)⁴ = 3.1604 ···. The even less accurate value of π = 3 is implied by some Babylonian formulas.³ Another incorrect formula found in ancient Babylonian mathematics is one that says that the volume of a frustum of a cone or of a square pyramid is given by the product of the altitude and half the sum of the bases. It seems that the Babylonians also used, for the area of a quadrilateral having a, b, c, d for its consecutive sides, the incorrect formula K =(a + c)(b + d)/4. This formula gives the correct result only if the quadrilateral is a rectangle; in every other instance the formula gives too large an answer. It is curious that this same incorrect formula was reproduced 2000 years later in an Egyptian inscription found in the tomb of Ptolemy XI, who died in 51 B.C.

In general, simple empirical reasoning may be described as the formulation of conclusions based upon experience or observation; no real understanding is involved, and the logical element does not appear. Empirical reasoning often entails stodgy fiddling with special cases, observation of coincidences, experience at good guessing, considerable experimentation, and flashes of intuition. Perhaps a very simple hypothetical illustration of empirical reasoning might clarify what is meant by this type of procedure.

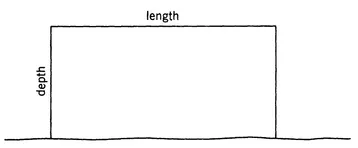
Suppose a farmer wishes to enclose with 200 feet of fencing a rectangular field of greatest possible area along a straight river bank, no fencing being required along the river side of the field. If we designate as the depth of the field the dimension of the field perpendicular to the river bank and as the length of the field the dimension parallel to the river bank (see Figure 1.1), the farmer could soon form the following table:

Depth in feet	Length in feet	Area in square feet
10	180	1800
20	160	3200
30	140	4200
40	120	4800
50	100	5000
60	80	4800
70	60	4200
80	40	3200
90	20	1800

Examination of the table shows that the maximum area recorded occurs when the depth is 50 feet and the length is 100 feet. The interested farmer might now try various depths close to, but on each side of, 50 and would perhaps make the following additional table:

Depth	Length	Area
48	104	4992
49	102	4998
50	100	5000
51	98	4998
52	96	4992

FIGURE 1.1

By now the farmer would feel quite certain that the maximum area is obtained when the depth is 50 feet and the length is 100 feet; that is, he would accept the proposition that the maximum area occurs when the length of the field is twice the depth of the field. A further strengthening of this belief would result from his examination of the symmetry observed in his table, and he would no doubt use his conjecture and pass it along to others as a reliable mathematical fact. Of course, the farmer’s conclusion is by no means established, and no present-day student of mathematics would be permitted to “prove” the conjecture in this fashion. Shrewd guessing has taken the place of deductive logic; patience has replaced brilliance.

In spite of the empirical nature of ancient oriental mathematics, with its complete neglect of proof and the seemingly little attention paid to the difference between exact and approximate truth, one is nevertheless struck by the extent and the diversity of the problems successfully attacked. Particularly has this become evident in recent years with the scholarly deciphering of many Babylonian mathematical tablets. Apparently a great deal of elementary mathematical truth can be discovered by empirical methods when supplemented by extensive experimentation carried on patiently over a long period of time.

How were the mathematical findings of the ancient orient stated? Here we must rely on such primary sources as the Rhind, the Moscow, and other Egyptian mathematical papyri and on the approximately three hundred Babylonian mathematical tablets that have so far been deciphered.

The Rhind, or Ahmes, papyrus is a mathematical text dating from about 1650 B.C. Partaking of the nature of a practical handbook, it contains 85 problems copied by the scribe Ahmes from a still earlier work. Now possessed by the British Museum, it was originally purchased in Egypt by the Scottish antiquarian, A. Henry Rhind. This papyrus and the somewhat older Moscow papyrus, a similar mathematical text containing 25 problems, constitute our chief sources of information concerning ancient Egyptian mathematics. All of the 110 problems found in these papyri are numerical, and many of them are very easy. In general, each problem is first formulated and then followed by a step-by-step solution using the special numbers given at the beginning. Although special numbers are employed in thi...