Mind Tools

The Five Levels of Mathematical Reality

Rudy Rucker

• Editorial: Dover Publications
• Año: 2013
• ISBN:
  9780486782195
• Categoría: Mathematics
• Categoría: History & Philosophy of Mathematics

This reader-friendly volume groups the patterns of mathematics into five archetypes: numbers, space, logic, infinity, and information. Rudy Rucker presents an accessible introduction to each of these important areas, reflecting intelligence gathered from the frontiers of mathematical thought. More than 100 drawings illuminate explorations of digital versus analog processes, logic as a computing tool, communication as information transmission, and other `mind tools.`
`Mind Tools is an original and fascinating look at various aspects of mathematics that is sure to fascinate the nonmathematician.` — Isaac Asimov
`A lighthearted romp through contemporary mathematics. . . . Mind Tools is a delight.` — San Francisco Chronicle
`For those who gave up college mathematics for what seemed more liberal arts, Rudy Rucker's book, Mind Tools, is a dazzling refresher course. . . . He rekindles the wonder that can come from contemplating logarithms, exponential curves and transcendental numbers.` — The New York Times Book Review
`One of Rucker's greatest assets is his ability to make complexities comprehensible to the general reader without lecturing.` — The Washington Post
`Approaching all of mathematics, and everything else, by way of information theory, Dr. Rucker's latest and most exciting book opens vistas of dazzling beauty — scenes that blend order with chaos, reality with fantasy, that startle you with their depths of impenetrable mystery.` — Martin Gardner

1

NUMBER

Zero and One

For one reason or another, we humans very commonly use 0 and 1 as an example of the most basic possible type of distinction. We think in terms of many other such distinctions — off and on, negative and positive, night and day, woman and man — but, at least to a mathematician, zero and one have a special appeal.

What is it about zero and one? Suppose I free-associate a little.

I think it is significant that the international hand gesture for coitus consists of a forefinger (1) bustling in a thumb and forefinger loop (0). This key archetype finds socially acceptable expression as the fat lady and the thin man. The symbol 0 seems egg-like, female, while 1 is spermlike and male. Can this really be an accident? A study of the history of mathematics shows that our present-day symbols were only adopted after centuries of trial and error. It seems likely that the symbols to survive are those that best “fit” our ingrained modes of thought.

An egg is round, and a sperm is skinny. There’s only one egg, but there are lots and lots of sperm. The sperm are active, while the egg just waits. The lovely round woman is besieged by suitors seeking rest, seeking completion.

Formally speaking, both zero and one are undefinable. The primitive concepts “nothing” and “something” cannot be explained in terms of anything simpler. We understand these concepts only because they are built into the world we live in.

Before the beginning of time, the universe is like a 0, an egg. The egg hatches, and out comes 1, the chicken. Chickens here, chickens there, chickens, chickens everywhere.

Why, incidentally, does the egg hatch? Why is there something instead of nothing? Well, if there weren’t any somethings, then we wouldn’t be here asking about it… . Is this enough of an answer?

Occasionally, in moments of deep absorption, all distinctions may seem to fall away, and you do have a kind of 0 experience. As long as you are, in some sense, in touch with the void, you aren’t going to be asking, “Why is there something instead of nothing?” But the moment passes, and you’re a regular person again. Cluck, cluck.

One and zero are like Punch and Judy, endlessly acting their play. What is perhaps astonishing is that mankind has managed to build up a science based on this play: the science of number.

Numbers and Logs

The simplest possible numeration system is the “tally” system. Here a number N is represented by a list of N ones. Ordinary finger-counting uses this system (Fig. 20).

The tally system is awkward for expressing big numbers. The Roman numeration system is considerably more efficient. Recall that the Romans used I, V, X, L, C, D, and M to stand for, respectively, 1, 5, 10, 50, 100, 500, and 1000. Writing X instead of 1111111111 is a big savings. One flaw with the Roman system is that you can’t always read a Roman number one letter at a time — to know that IV is 4 and LX is sixty, you have to see two letters together. This makes Roman numbers hard to read. How many of us have seen the Roman number MDCCLXXVI on the back of a dollar bill without realizing that it’s supposed to be 1776? Another problem with the Roman system is that it peters out at M, so that if I want to express eleven thousand, I have to write MMMMMMMMMMM. Out past M, something like the tally system sets in again.

These days, every advanced culture on Earth uses the familiar base-ten system of numeration. Quantities are expressed as sums of units, groups of ten, groups of ten tens, groups of ten groups of ten tens, and so on:

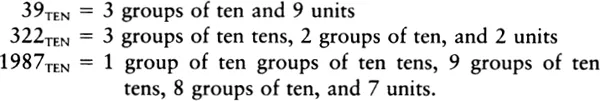
The subscript “TEN” is a reminder that our number system is based on groupings of ten. It is a little hard to grasp that there is nothing sacred about the base-ten numeration system. Simple-minded as it may seem, the only reason we use ten is that we have ten fingers. A numeration system could equally well be based on, say, three — with groups of three, groups of three threes, groups of three groups of three threes, and so on. To make this clear, take a look at the different ways in which 54 units are broken up and described in numeration systems based on two through ten.

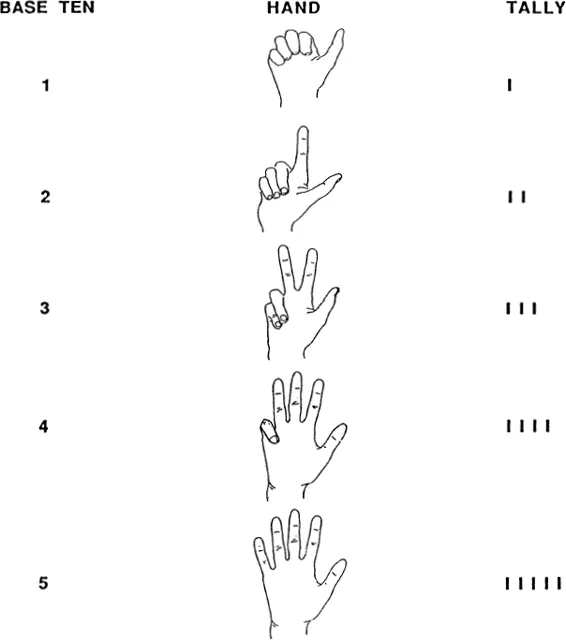
Fig. 20 Counting to five.

Digital computers use the “binary” or base-two number system. One reason for this is that computer memories are based on internal switches which can be set two ways: on or off. By letting on be 1 and off be 0, computers can represent numbers by setting their memory switches in various arrangements.

Fig. 21 54 in different number bases.

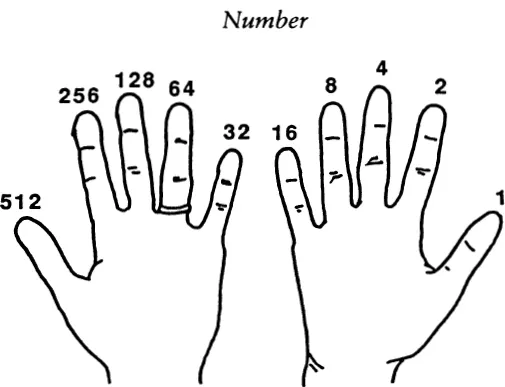
Fig. 22 Fingers as base-two flip-flops.

By applying a binary system to the positions of your ten fingers, you can actually count up to 1,023. This is done as follows. Lay your two hands down side by side, palms up as in Fig. 22. Running from right to left, associate each digit with a successive number from the “doubling sequence”: 1, 2, 4, 8, 16, 32, 64, 128, 256, and 512. These are, of course, powers of two. The “grouping by twos” process suggested in Fig. 21 indicates that each whole number can be represented in a unique way as a sum of some numbers from the doubling sequence.

If you stick up the appropriate finger for each doubling-sequence number used in a given number’s breakdown, you get a finger pattern specific to that number, as illustrated in Fig. 23. To the right of the finger patterns, I have written the corresponding base-two notation for each pattern.

Using only one hand, you can represent any number between 00000_TWO and 11111_TWO, which is any number between 0 and 31_TEN; 32_TEN possibilities in all. If you use your toes as well as your hands (though raising and lowering toes is not easy) you could reach 1111111111111111111l_TWO? which is 1,048,576_TEN, or a bit more than a million.

If we try to base a numeration system on one, we end up with the tally system, because all powers of 1 are equal to 1. Two then has the virtue of being the smallest number that can be used as the base of a numeration system. For purposes of analyzing how much information a decision among N possibilities involves, it is good to think in terms of base two.

To choose among thirty-two possibilities is to make five 0/1 choices in writing out a five-digit binary number. Another way of putting this is to say that a choice among thirty-two possibilities requires five bits of information, where a bit of information is a single choice between0 and 1. It is significant that thirty-two is two to the fifth power, and a choice among thirty-two possibilities takes five bits of information. In general, choosing among two to the N possibilities requires N bits of information. Making the choice is like selecting a path along a path that has N binary forks in it.

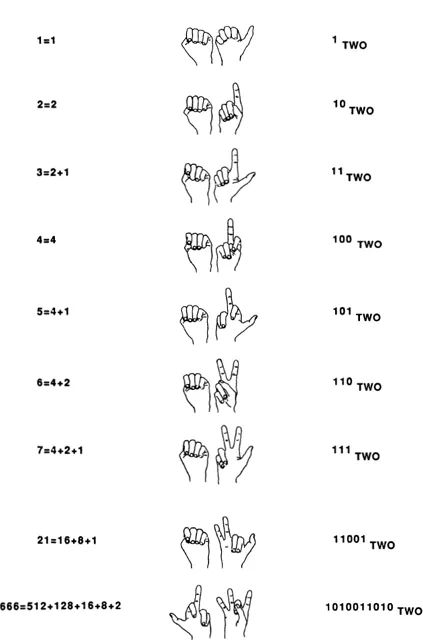
Fig. 23 Base-two finger counting.

To express this insight more clearly, we need to talk about logarithms. Information theory is usually formulated in terms of logarithms. In the past, this always put me off; like anyone else, I hated logarithms, but then I had a key insight: the logarithm of a number is approximately equal to the number of digits it takes to write the number out. In base ten, log 10 is 1, log 100 is 2, log 1987 is about 3, log 12345 is about 5, and the log of one billion is 10.

Formally, we define the logarithm operation as the inverse of exponentiation. In base ten, the logarithm of a number N is precisely the power to which ten would have to be raised to equal N.

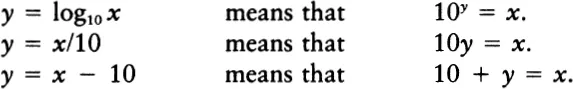
We don’t have to base our logarithms on ten. When we are doinginformation theory, it is much better to base our logarithms on two. In base two, the logarithm of a number N is precisely the power to which two would have to be raised to equal N:

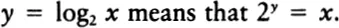
No matter what base we use, logarithms have a number of very beautiful properties. Three properties that make logarithms useful for calculation are

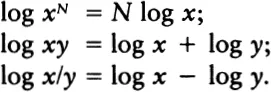
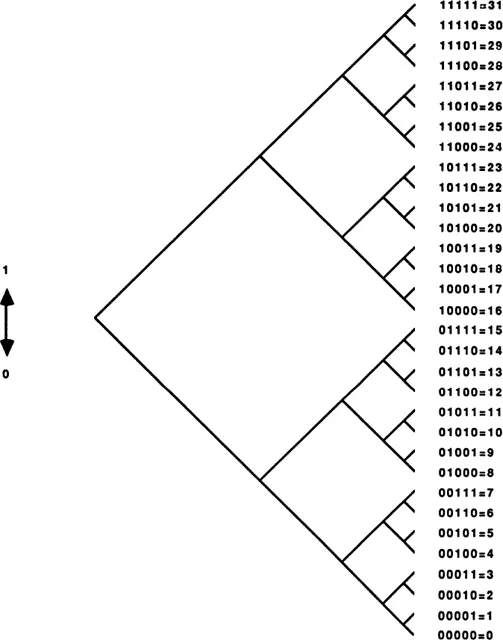
Fig. 24 Five 0/1 choices give thirty-two outcomes.

In the old days, people used to compute a large product like 1987 × 7891 by looking up log 1987 and log 7891, adding the logs, and looking up the number whose log is equal to the sum. The computation was done either by means of a log-antilog table, or by means of a slide rule. A slide rule basically consists of two identical sticks printed with number names in such a way that a number’s name appears at a position whose actual distance from the stick’s end is the logarithm of the number. Products are computed by the analog process of measuring off the corresponding stick lengths. Electronic calculators actually do their work by using logarithms, though one doesn’t notice this except when the hidden log-antilog steps lead to round-off errors such as saying “1.9999999” when “2” is meant.

It is often useful to draw graphs in which one or both axes are scaled logarithmically. Looking at the graphs on page 48 makes it clear that, working in any given base, the number of digits it takes to write a number N lies between log N and (log N) + 1.

Fig. 25 A slide rule in action.

The reason informati...