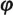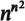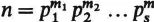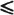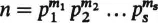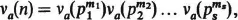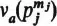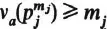A Course on Group Theory

John S. Rose

• Editorial: Dover Publications
• Año: 2013
• ISBN:
  9780486170664
• Categoría: Mathematics
• Categoría: Group Theory

This textbook for advanced courses in group theory focuses on finite groups, with emphasis on the idea of group actions. Early chapters summarize presupposed facts, identify important themes, and establish the notation used throughout the book. Subsequent chapters explore the normal and arithmetical structures of groups as well as applications.
Topics include the normal structure of groups: subgroups; homomorphisms and quotients; series; direct products and the structure of finitely generated Abelian groups; and group action on groups. Additional subjects range from the arithmetical structure of groups to classical notions of transfer and splitting by means of group action arguments. More than 675 exercises, many accompanied by hints, illustrate and extend the material.

1

INTRODUCTION TO FINITE GROUP THEORY

The ideal aim of finite group theory is to ‘find’ all finite groups: that is, to show how to construct finite groups of every possible type, and to establish effective procedures which will determine whether two given finite groups are of the same type. The attainment of this ideal is of course quite beyond the reach of present techniques (though the corresponding aim for finite abelian groups was achieved a hundred years ago: see 8.24, 8.41). But what kind of programme might be devised towards the fulfilment of such an aim?

To each finite group G there is associated the positive integer | G|. We note two elementary facts.

1.1. For each positive integer n, there is at least one type of group of order n.

For instance, the set of complex nth roots of unity forms a (cyclic) group of order n under multiplication: see 2.14.

1.2. For each positive integer n, there are only finitely many different types of groups of order n.

To see this we observe that for any group G of order n and any set X of n elements, X can be given the structure of a group isomorphic to G. All that is needed is to choose some bijective map

: G → X and then to define multiplication in X by the rule (g₁

)(g₂

) = (g₁g₂)

for all g₁, g₂∈G. It is straightforward to check that this multiplication on X satisfies the group axioms; then also, by definition,

becomes an isomorphism. This means that groups of order n of all possible types appear among all possible assignments of a binary operation to any particular set of n elements. But the number of different such assignments is

, and so this is also an upper bound for the number of types of groups of order n.

(For another proof of 1.2, see 4.24.) For each positive integer n, let v(n) denote the number of types of groups of order n. Very little is known about v(n) in general (see 301 for a sharper upper bound on v(n)); but one simple remark can be made immediately. It follows from Lagrange’s theorem that a group of prime order must be cyclic (1). Since any two cyclic groups of the same order are isomorphic (2), we have

1.3. For each prime number p, v(p) = 1.

There are numbers n other than primes for which v(n) = 1. We mention a result which characterizes these numbers – though the result is not of importance in group theory, but merely a curiosity (see 575).

1.4. Let

, where s, m₁,…, m_s are positive integers and p₁,…, p_s distinct primes. Then v(n) = 1 if and only if m₁ = m₂ = … = m_s = 1 and for all i,j = 1,…, s, p_i − 1 is not divisible by p_j.

(Thus for example v(15) = 1; see 215.)

Now, for each positive integer n, let v_a(n) denote the number of types of abelian groups of order n: then v_a(n)

v(n). From theorems on the structure of finite abelian groups (see 8.43), we have

1.5. Let

, where s,m₁,…,m_s are positive integers and p₁,…,p_s distinct primes. Then

and, for each j = 1,…, s,

is the number of partitions of m_j; that is, the number of ways of expressing m_j as a sum of positive integers (the order of components being disregarded). In particular,

.

This shows that there is no upper bound for v_a(n) which is independent of n; and hence also no upper bound for v(n) in...