Tópicos previos a la matemática superior

Herrón Osorio, Sigifredo De Jesús, Sigifredo De Jesús Herrón Osorio

• Editorial: Universidad Nacional de Colombia
• Año: 2014
• ISBN del libro electrónico:
  9789587617627
• Categoría: Mathematics
• Categoría: Mathematics General

El libro es adecuado para estudiantes de matemáticas y también es un sólido soporte para estudiantes de disciplinas afines que deben enfrentar cursos de matemáticas en su formación profesional. El texto reúne algunos temas de varias asignaturas como: teoría de conjuntos, teoría de conjuntos, teoría de números, fundamentos de matemáticas, análisis matemático y topología de la recta. Cumple con el objetivo de introducir los sistemas numéricos más importantes utilizados en el área. Es un buen libro de referencia o de refuerzo. Además, presenta una buena cantidad de ejercicios que complementa de forma muy natural, la teoría expuesta en cada uno de los capítulos. La rigurosidad en el tratamiento de los temas y las demostraciones es exquisita, es un buen punto de referencia para usar cuando se necesite información acerca de los sistemas numéricos más utilizados. Tiene una escritura impecable, su redacción es adecuada y es un texto fácil de leer y entender para un estudiante de matemáticas. Es un texto que de manera sencilla y sin perder el rigor de la matemática formal, introduce una secuencia de tópicos desde las nociones de operación binaria y clases de equivalencia, necesarios para una construcción formal de los números reales usando sucesiones, hasta finalmente, introducir los números complejos.

Capítulo 1

Operaciones binarias

En este primer capítulo presentamos algunos elementos básicos que serán de uso rutinario en algunos capítulos posteriores. El presente capítulo concierne solamente a cierto tipo de funciones que en la práctica no se usan como tales y son llamadas operaciones binarias.

1.1 Operaciones binarias

Dado un conjunto no vacío A y un par de elementos a y b en este conjunto, si existe alguna manera * de operar con ellos y que el único resultado obtenido sea un elemento del conjunto dado, entonces llamaremos a * una operación binaria en dicho conjunto. Es decir, para a*b ∈ A, se tiene que el resultado a * b € A. Esto no es más ni menos que una función de A × A en A. Formalizamos entonces esta noción en la definición siguiente:

Definición 1.1. Sea A un conjunto no vacío. Una función de la forma * : A × A→ A se llama una operación binaria en A.

Una operación binaria también se llama clausurativa o ley de composición interna.

Se acostumbra escribir la evaluación de * en el par (a,b) ∈ A × A como a * b en lugar de * (a, b).

Ejemplo 1.2. Fijemos un conjunto A y sea A = P(A), el conjunto potencia o partes de A. La unión entre conjuntos “∪” y la intersección entre conjuntos “∩ ” son operaciones binarias en P(A).

Ejemplo 1.3. Sean A = {a,b,c} y * : A × A → A definida por la siguiente tabla:

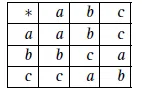
La función *, así definida, es una operación binaria en A.

Presentamos ahora algunas propiedades que pueden tener las operaciones binarias.

Definición 1.4. Sea * una operación binaria en A. Decimos que dicha operación es conmutativa si a * b = b * a para todo a,b ∈ A. Dicha operación se llama asociativa si a * (b * c) = (a * b) * c, para todo a, b, c ∈ A.

Por ejemplo, de lo que sabemos de la teoría de conjuntos, las operaciones binarias del Ejemplo 1.2 son conmutativas y asociativas. Un chequeo directo nos permite ver que la operación * del Ejemplo 1.3 es conmutativa. ¿Es dicha operación asociativa?

Definición 1.5. Sea * una operación binaria en A. Decimos que esta operación satisface la propiedad modulativa o que posee elemento neutro, si existe un elemento e ∈ A tal que e * a = a * e = a para todo a ∈ A.

En el Ejemplo 1.2 la operación binaria “∪” tiene al conjunto vacío como elemento neutro, ya que Ø ∈ P(A) = A y para todo X ∈ A se tiene que X ∪ Ø = Ø∪X = X. Mientras que la operación binaria “∩” tiene al conjunto fijo A como elemento neutro, ya que A ∈ P (A) = A y para todo X ∈ A se tiene que X ∩ A = A ∩ X = X. ¿Cuál es el elemento neutro en el Ejemplo 1.3?

Definición 1.6. Sea * una operación binaria en A con elemento neutro e ∈ A. Decimos que a ∈ A posee inverso lateral a izquierda si existe a′ ∈ A tal que a′ * a = e. Si existe a′′ ∈ A tal que a * a′′ = e decimos que a ∈ A posee inverso lateral a derecha. En caso de que los inversos laterales a izquierda y a derecha sean iguales, decimos que a′ es un inverso bilateral de a ∈ A. Si todo elemento de A tiene un inverso bilateral, decimos que la operación * es invertiva.

A manera de ilustración, ...

Índice

• Portada
• Portadilla
• Página legal
• Anotación
• Prólogo
• Capítulo 1
• Capítulo 2
• Capítulo 3
• Capítulo 4
• Capítulo 5
• Capítulo 6
• Bibliografía
• Apéndice
• Página institucional
• Créditos