¿Cómo aprendemos?

Los cuatro pilares con los que la educación puede potenciar los talentos de nuestro cerebro

Stanislas Dehaene, María Josefina D'Alessio

• Editorial: Siglo XXI Editores
• Año: 2019
• ISBN del libro electrónico: 9789876299749
• Categoría: Ciencias biológicas
• Categoría: Gestión del aula

El cerebro humano es una máquina extraordinaria, capaz de transformarse a sí misma a partir de la experiencia y de albergar talentos que nos vuelven únicos como especie: lenguaje, lectura, matemáticas, creación artística. La más asombrosa de sus facultades es sin dudas la del aprendizaje, aquella que nos permite no solo adaptarnos a las circunstancias, sino también lanzarnos con entusiasmo en busca de lo desconocido.

Un bebé aprende más rápido y más profundo que cualquier dispositivo de inteligencia artificial. Y por si esto fuera poco, los seres humanos han inventado un medio de inconmensurable eficacia para expandir su fabulosa capacidad. ¿Robots inteligentes? ¿Supercomputadoras? No: la escuela, esa poderosa institución de alcance masivo que acelera el desarrollo de nuestras habilidades y la transmisión del conocimiento acumulado por generaciones.

Reuniendo aportes de las neurociencias, la psicología cognitiva, la informática y la pedagogía, ¿Cómo aprendemos? explora en detalle las investigaciones acerca del aprendizaje y sus fundamentos biológicos: ¿cuáles son los procesos neuronales implicados?, ¿por qué la infancia y la juventud son tan sensibles?, ¿podemos seguir aprendiendo toda la vida?, ¿cuánto hay de innato y cuánto de adquirido en los dominios más relevantes de nuestro conocimiento? ¿Todos somos iguales a la hora de aprender? ¿Cuál es el rol de la memoria, de la atención? ¿Qué papel cumplen la nutrición, el sueño o la actividad física en el desarrollo? ¿Qué función tiene el error?

De la mano de los cuatro pilares del aprendizaje –la atención, el compromiso activo, el buen feedback y la consolidación–, Stanislas Dehaene lleva recomendaciones precisas para implementar en la familia y en la escuela de manera cotidiana.

Parte II

Cómo aprende nuestro cerebro

Esta facultad, existente en el alma de cada uno, y el órgano con que cada cual aprende, deben volverse, apartándose de lo que nace, con el alma entera, […] hasta que se hallen en condiciones de afrontar la contemplación del ser.

Platón, La República (~380 a.C.)

3. El saber invisible: las sorprendentes intuiciones de los bebés

¿Existe algo que parezca más indefenso que un recién nacido? ¿No parece completamente razonable pensar, como Locke, que su mente es una tabula rasa que espera recibir la huella del ambiente? Rousseau intentó resolver esta cuestión en su tratado Emilio o De la educación (1762): “Nacemos con capacidad para aprender, pero sin saber nada, sin conocer nada”. Cerca de dos siglos más tarde, la hipótesis fue retomada por Alan Turing, padre de la informática contemporánea: “Es verosímil que el cerebro del niño sea como una libreta que acabamos de comprar en la papelería. Un mecanismo muy pequeño y un montón de páginas en blanco”.

Hoy en día sabemos que esto es falso. Las apariencias engañan: pese a su inmadurez, el cerebro del recién nacido posee ya un amplio saber, heredado de su historia evolutiva. Sin embargo, la mayor parte de este conocimiento permanece invisible, ya que no se expresa en el comportamiento primitivo del bebé. Hicieron falta avances metodológicos importantes en el dominio de las ciencias cognitivas para poner en evidencia el extraordinario repertorio de capacidades con que cada bebé llega al mundo. Objetos, números, probabilidades, rostros, lenguaje… El alcance de los conocimientos innatos de los bebés está lejos de ser despreciable.

El concepto de objeto

Tenemos la intuición de que el mundo está hecho de objetos rígidos. En realidad, está constituido por átomos, pero en la dimensión en que vivimos, estos átomos se aglomeran y suelen comportarse como entidades coherentes que se mueven juntas y que a veces se entrechocan sin perder su cohesión; estos grandes haces de átomos forman lo que llamamos “objetos”. La existencia de los objetos es una propiedad fundamental de nuestro ambiente. ¿Tenemos que aprender esto? No. Millones de años de evolución parecen haber integrado este conocimiento en lo más profundo de nuestros cerebros. Desde que tiene unos pocos meses de vida, el bebé ya sabe que el mundo está formado por objetos, que se mueven como un bloque, que ocupan espacio, que no pueden desaparecer sin motivo, y que es imposible que dos de ellos ocupen un mismo lugar (Baillargeon y DeVos, 1991; Kellman y Spelke, 1983). En cierto sentido, su cerebro ya conoce las leyes de la física: espera que la trayectoria de un objeto, tanto en el espacio como en el tiempo, sea continua, sin desapariciones ni saltos repentinos.

¿Cómo lo sabemos? Porque los bebés manifiestan sorpresa en situaciones experimentales que violan las leyes de la física. Actualmente, en los laboratorios de ciencias cognitivas, los investigadores se transforman en ilusionistas (figura 7). Usan teatrinos especialmente creados para bebés y despliegan todos los trucos y las materializaciones de consumados prestidigitadores; hay objetos que aparecen, desaparecen, se multiplican, se disuelven… Cámaras ocultas monitorean los experimentos y los resultados son claros: hasta los bebés de unas pocas semanas son sensibles a la magia. Ya poseen intuiciones profundas acerca del mundo físico y, como todos nosotros, se quedan estupefactos cuando estas se refutan o quebrantan. Al hacer zoom en los ojos del niño, para así confirmar hacia dónde se orienta su mirada y durante cuánto tiempo, los investigadores logran medir el grado de sorpresa y deducir qué era lo que la criatura esperaba ver.

Les propongo que escondan un objeto detrás de un libro y luego, con un golpe seco, lo aplasten, como si ese objeto ya no existiera (en realidad, lo habrán hecho salir por una pequeña puerta trampa), y entonces lo comprobarán: ¡los bebés se quedan estupefactos! No logran comprender que algo sólido pueda evaporarse sin dejar huellas. También se sorprenden cuando un objeto desaparece detrás de una pantalla y reaparece detrás de otra, sin que lo hayan visto franquear el espacio vacío entre las dos. Del mismo modo, los desconcierta que un pequeño tren descienda por una pendiente y atraviese una pared rígida sin que esta lo detenga. Esperan que un objeto forme un todo coherente: si ven dos extremidades de una varilla moverse con coherencia de los dos lados de una pantalla, imaginan que pertenecen a una sola varilla, y se muestran muy sorprendidos cuando la pantalla se baja y deja ver dos varillas distintas (figura 8).

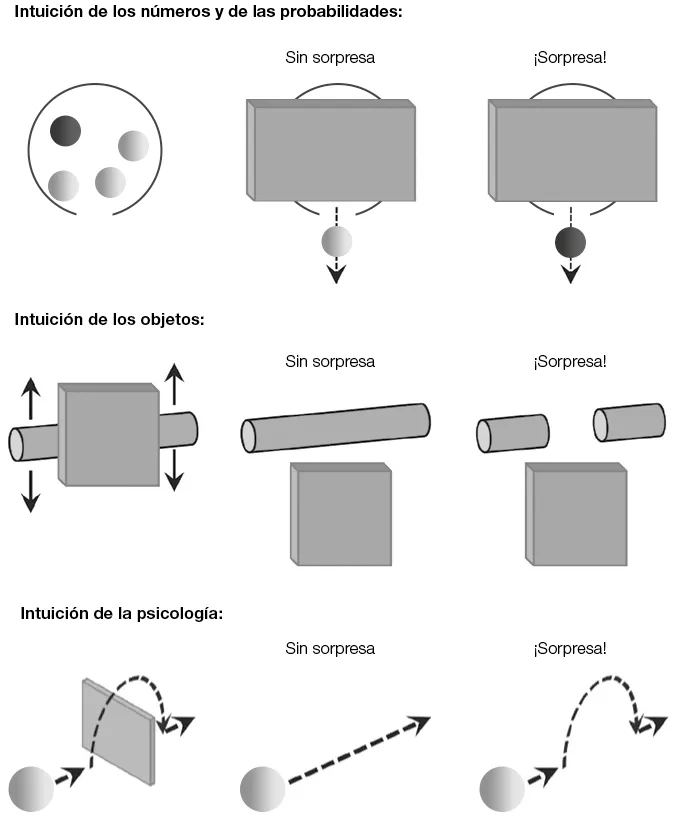
Figura 7. Lejos de ser pizarras vírgenes de conocimiento, los bebés poseen amplios saberes en cuestiones de física, aritmética, probabilidad o geometría. En el laboratorio, cuando se los somete a situaciones que violan las reglas de estos campos, la medida de su sorpresa revela la sofisticación de sus intuiciones acerca del mundo.

Figura 8. Para evaluar las intuiciones de los bebés, se determina si miran durante más tiempo una escena sorprendente. Cuando en una caja hay mayoría de objetos blancos, el bebé se sorprende cuando ve salir de ella un objeto negro (intuición de los números y de las probabilidades). Si dos extremos de una varilla se mueven de forma coherente, el bebé se queda anonadado cuando se pone en evidencia que en realidad son dos objetos diferentes (intuición de los objetos). Y si una esfera salta de forma espontánea por encima de un muro, el bebé deduce que se trata de un ser animado dotado de una intención (en este caso, la de moverse hacia la derecha) y se queda atónito al ver que la esfera continúa saltando cuando el muro ya no está (intuición de la psicología: ¿para qué debería saltar un obstáculo inexistente?).

Esto demuestra que los bebés poseen un vasto saber acerca del mundo, aunque no conocen todo desde el principio, ni mucho menos. Hacen falta algunos meses para que los bebés comprendan cómo dos objetos se sostienen el uno al otro (Baillargeon, Needham y Devos, 1992; Hespos y Baillargeon, 2008). Al principio, ignoran que un objeto se cae cuando lo sueltan. Solo muy gradualmente toman conciencia de todos los factores que causan que un objeto se caiga o no se caiga. En un primer momento, se dan cuenta de que los objetos se caen cuando pierden su apoyo, pero creen que es suficiente cualquier tipo de contacto para mantenerlos quietos, por ejemplo, cuando ponemos un juguete al borde de una mesa. Poco a poco, descubren que el objeto no solo debe estar en contacto con la mesa, sino que es necesario que esté bien puesto ahí: ni debajo, ni al lado, sino sobre la mesa misma. Y todavía les harán falta algunos meses para descubrir que esta regla no es suficiente: lo que debe apoyarse arriba de la mesa es el centro de gravedad del objeto.

Piensen en esto la próxima vez que se desesperen al ver que su bebé deja caer, por décima vez, la cuchara mientras almuerza. ¡Solamente está experimentando! Como cualquier científico, necesita realizar una serie de experiencias para rechazar, una tras otra, todas las teorías incorrectas que postulan que

1. los objetos se sostienen por sí solos en el aire;
2. es suficiente que se toquen con otro para no caerse;
3. es suficiente que estén arriba de otro para no caerse;
4. la mayor parte del volumen del objeto debe estar encima de otro para no caerse; y así sucesivamente.

Esta actitud experimental no se extingue en la edad adulta. Nos encantan todos los dispositivos que parecen desobedecer las leyes habituales de la física (globos de helio, móviles en equilibrio, un móvil con un centro de gravedad periférico…) y disfrutamos de los espectáculos de ilusionismo en que los conejos desaparecen en un sombrero y las asistentes son cortadas en dos. Si estas situaciones nos divierten, es porque violan las intuiciones que poseemos desde el nacimiento y que hemos refinado durante el primer año de vida. Joshua Tenenbaum, especialista en inteligencia artificial del Massachusetts Institute of Technology (MIT), propuso la hipótesis de que los bebés tienen un motor físico en la cabeza, un modelo mental del comportamiento de los objetos que se asemeja al utilizado por los programas de videojuegos para simular mundos virtuales. Al hacer funcionar esas simulaciones dentro de su cabeza y compararlas con la realidad, los bebés descubren, muy temprano, lo que es físicamente posible o probable.

El sentido del número

Tomemos un segundo ejemplo: la aritmética. ¿Existe algo más evidente para nosotros que el hecho de que un bebé lo ignora todo acerca de las matemáticas? Y sin embargo, desde la década de 1980, existen experimentos que demuestran lo contrario (Izard, Dehaene-Lambertz y Dehaene, 2008; Izard y otros, 2009; Starkey y Cooper, 1980; Starkey, Spelke y Gelman, 1990).[13] En uno de ellos, se presentan reiteradas veces ante los bebés imágenes que muestran dos objetos. Después de un rato, se aburren… hasta que se les muestra una tarjeta con tres objetos: con la atención renovada, se quedan mirando esta nueva escena durante más tiempo, lo que pone de manifiesto que detectaron el cambio. Al manipular la índole, el tamaño y la densidad de los objetos, podemos probar que los niños perciben el número abstracto, el numeral cardinal del conjunto, y no tal o cual parámetro físico. La mejor prueba de que poseen este abstracto “sentido del número” es que generalizan de los sonidos a las imágenes: si escuchan tu tu tu tu, vale decir, cuatro sonidos, se interesan en una imagen que también tenga cuatro objetos, en lugar de prestar atención a una en que hay doce, y viceversa (Izard y otros, 2009). Los experimentos bien controlados, como este, abundan y demuestran que, desde el nacimiento, los bebés tienen la capacidad de reconocer de manera intuitiva un número aproximativo, sin contar, ya sea que la información provenga del oído o de la vista.

¿Los bebés también pueden calcular? Supongan ahora que un niño ve un primer objeto desaparecer detrás de una pantalla, y a este lo sigue un segundo objeto. A continuación, la pantalla se baja… ¡y resulta que hay solo un objeto! Los bebés expresan su sorpresa mediante una prolongada investigación de la escena inesperada (Koechlin, Dehaene y Mehler, 1997; Wynn, 1992). En cambio, si ven los dos objetos esperados, no le dedican más que un breve vistazo. Este comportamiento de “sorpresa cognitiva”, en reacción a la violación de un cálculo mental, muestra que, desde los pocos meses de vida, el niño comprende que 1 + 1 debería ser 2. Lo que ocurre es que el bebé construye un modelo interno de la escena escondida, y sabe manipularlo agregándole o quitándole objetos. Y eso funciona para 1 + 1 y 2 - 1, pero también para 5 + 5 y 10 - 5… Siempre que el error es lo suficientemente grande, un bebé de 9 meses se sorprende si la pantalla presenta un cálculo incorrecto: infiere que 5 + 5 no puede ser 5, y que 10 - 5 no puede ser 10 (McCrink y Wynn, 2004).

¿Se trata en efecto de una capacidad innata? ¿Pueden ser suficientes los primeros meses de vida para que el niño aprenda el comportamiento de conjuntos de objetos? Si bien no cabe duda de que, con el transcurso de los meses, el niño refina la precisión con que percibe el número (Halberda y Feigenson, 2008; Piazza y otros, 2010, 2013), los datos también demuestran con plena claridad que el punto de partida no es una tabula rasa. Los recién nacidos perciben los números desde que tienen pocas horas de vida, y lo mismo ocurre con los monos, las palomas, los cuervos, las salamandras, los pollitos y hasta los peces. En el caso de los pollitos, los científicos pueden controlar todos los estímulos sensoriales desde el momento en que se rompe el huevo: el pequeño pollito no ha visto un solo objeto… y, sin embargo, reconoce los números (Rugani y otros, 2009, 2015).

Estos experimentos demuestran que la aritmética forma parte de las competencias innatas que la evolución otorga a numerosas especies, incluida la humana. Se detectó un circuito cerebral para los números en el mono y también en el cuervo. Sus cerebros albergan “neuronas numéricas” que se comportan de manera muy similar: son sensibles a cantidades específicas de objetos. Algunas neuronas prefieren ver un objeto, otras dos, tres, cinco o incluso treinta, y estas células están presentes aun entre los animales que no han recibido entrenamiento específico (Ditz y Nieder, 2015; Viswanathan y Nieder, 2013). Mi laboratorio usó técnicas de imágenes del cerebro para poner en evidencia que en ubicaciones homólogas del cerebro humano los circuitos neuronales incluyen células similares especializadas en el cardinal de un conjunto concreto; además, en fecha reciente, gracias a los avances en las técnicas de registro, se tomaron imágenes directas de esas neuronas en el hipocampo humano (Piazza y otros, 2004; Kutter y otros, 2018).

De paso, estos resultados echan por tierra una de las principales teorías del desarrollo del niño, la del gran psicólogo suizo Jean Piaget, quien consideraba que los bebés ignoraban la “permanencia del objeto” –el hecho de que el objeto continúa existiendo cuando no lo vemos– y que esta capacidad recién aparecía hacia finales del primer año. Pensaba también que el concepto abstracto del número estaba fuera del alcance de los niños de escasos años de vida, y que lo aprendían lentamente por obra de una gradual abstracción de las medidas más concretas de tamaño, longitud o densidad. En realidad, es exactamente a la inversa. Los conceptos de objeto y de número son características fundamentales de nuestro pensamiento, forman parte del “núcleo de conocimientos” con que llegamos al mundo y que, por sus combinaciones, nos permite formular razonamientos más complejos (Spelke, 2003).

El sentido del número es solo un ejemplo de lo que llamo “saber invisible” de los niños, esas intuiciones precoces que poseen desde el nacimiento y que guían todos sus aprendizajes. Veamos otros ejemplos de las competencias que los investigadores demostraron que tienen los bebés de algunas pocas semanas de vida.

La intuición de las probabilidades

Del número a la probabilidad, no hay más que un paso… ¡que los investigadores dieron recientemente al preguntarse si los bebés de pocos meses podrían anticipar el resultado de un sorteo de lotería! En este experimento, se les presenta a los bebés una urna transparente llena de bolillas que se mueven al azar. La caja contiene cuatro bolillas: tres blancas y una negra (figura 8). En la parte inferior, hay una salida. En un momento dado, un cartel esconde la urna… y de allí sale una bolilla, o negra o blanca. Frente a esto, el nivel de sorpresa del niño está directamente relacionado con el grado de improbabilidad de lo que ve: si lo que sale es una bolilla blanca, vale decir, el acontecimiento más probable (dado que en la caja hay una mayoría de bolillas de ese color), el bebé mira apenas un breve instante… En cambio, si se presenta el evento improbable, la salida de una bolilla negra, que solo tenía una posibilidad sobre cuatro de producirse, la mira durante mucho más tiempo. Controles posteriores confirman que, en sus pequeñas cabezas, las niñas y los niños ponen en juego una detallada simulación mental de la situación y de las probabilidades asociadas. Así, si se introduce un panel que bloquea las bolillas, o si se aleja más o menos las bolillas de la salida, o bien se hace variar el lapso previo a la aparición de los objetos, el niño integra todos estos parámetros a su cálculo mental de probabilidades. Como en el caso de los objetos que desaparecían detrás de una pantalla, la duración de su mirada atenta refleja la improbabilidad de la situación observada: los niños parecen calcular esta improbabilidad sobre la base de la cantidad de objetos involucrados.

Todas estas competencias superan a las redes neuronales actuales. En efecto, la reacción de sorpresa de los niños dista de ser una respuesta trivial: indica que el cerebro fue capaz de hacer un cálculo de probabilidades y llegó a la conclusión de que el acontecimiento observado tenía una ínfima posibilidad de producirse. Si las miradas de los bebés presentan reacciones de sorpresa muy elaboradas, se debe a que sus cerebros son capaces de realizar cálculos probabilísticos. De hecho, hoy en día, una de las teorías más en boga sobre el funcionamiento del cerebro lo considera un calculador probabilístico que manipula las distribuciones de probabilidad y las utiliza para anticipar acontecimientos futuros. Los experimentos revelan que los bebés están equipados con este sofisticado calculador.

Una serie de experiencias recientes demuestra que el bebé ya posee todos los mecanismos para realizar inferencias probabilísticas complejas. ¿Recuerdan la teoría matemática del reverendo Bayes, esta teoría de las probabilidades que permite retrotraer una observación a sus causas probables? Bueno, un bebé de apenas algunos meses parece seguir esta regla en su razonamiento (Xu y García, 2008). En efecto, no solamente sabe pasar de la caja de bolillas de colores a las probabilidades correspondientes (un razonamiento hacia delante), como acabamos de ver, sino también de sus observaciones al contenido de la caja (un razonamiento en sentido inverso).

Un nuevo experimento: muéstrenle a un niño una caja opaca, sin que pueda ver su contenido. Después pídanle a una persona que, con los ojos tapados, extraiga al azar una serie de bolillas. Estas aparecen de a una, y se observa que la mayoría son rojas. ¿El bebé puede deduci...

Índice

• Cubierta
• Índice
• Portada
• Copyright
• Este libro (y esta colección)
• Dedicatoria
• Epígrafe
• Introducción a las ciencias del aprendizaje
• Parte I. ¿Qué es aprender?
• Parte II. Cómo aprende nuestro cerebro
• Parte III. Los cuatro pilares del aprendizaje
• Conclusión
• Agradecimientos
• Bibliografía
• Créditos de material gráfico