¿Determinismo o indeterminismo?

Grandes preguntas de la ciencia a la filosofía

Claudia Vanney, Juan Franck

• Editorial: Editorial UFV
• Año: 2018
• ISBN del libro electrónico: 9788418360039
• Categoría: Pedagogía
• Categoría: Teoría y práctica de la educación

El presente volumen es el resultado de un esfuerzo conjunto de tres años, durante los cuales físicos, biólogos, neurocientíficos y filósofos estudiaron el tema del determinismo con una mirada interdisciplinar. Los capítulos están escritos en coautoría por científicos y filósofos, y giran en torno a preguntas sobre problemas epistemológicos, ontológicos o filosóficos-teológicos.

OLIMPIA LOMBARDI¹ - RAFAEL A. MARTÍNEZ²

Ciencia y filosofía se han enfrentado, a lo largo de la historia, con el problema del determinismo: ¿está el comportamiento del mundo determinado de modo absoluto? ¿O existe en él un cierto margen de imprevisión o indeterminismo? Las primeras teorías científicas, a partir de la mecánica newtoniana, parecían inclinar la balanza hacia una imagen determinista. Sin embargo, solo podían describir con precisión y rigor algunos sistemas particulares, de tipo mecánico, electromagnético o químico. La casi totalidad de los sistemas reales resultaban mucho más complejos, y la visión determinista parecía inaplicable.

La situación cambia con el desarrollo de nuevas técnicas capaces de afrontar el estudio de los sistemas complejos dotados de inestabilidad intrínseca. Su estudio sistemático se origina en la década de 1960 gracias a la confluencia de dos factores. El primero de ellos, de índole socio-económica, fue el interés en la planificación agrícola y ganadera, lo cual exigía mejorar la predicción climática. Puesto que los sistemas meteorológicos son altamente inestables, su análisis requería fomentar el estudio de la inestabilidad desde un punto de vista teórico. No es casual, entonces, que haya sido precisamente un meteorólogo, Edward Lorenz, quien en 1963 obtuviera los primeros resultados cuantitativos a partir de un sistema de ecuaciones diferenciales correspondientes a una evolución altamente inestable. El segundo factor fue el desarrollo de la tecnología electrónica y, con ello, de las computadoras, lo que permitió superar las limitaciones impuestas por el carácter analíticamente intratable de las ecuaciones dinámicas de los sistemas altamente inestables. Mediante simulaciones numéricas adecuadas, fue posible brindar un tratamiento cuantitativo al concepto de inestabilidad y a los resultados cualitativos con los que se contaba hasta el momento.

Desde el punto de vista teórico, la alta inestabilidad se estudia mediante dos enfoques, la teoría del caos y la teoría ergódica, que parecen conducir a conclusiones contradictorias acerca del carácter determinista o indeterminista de la realidad. El presente trabajo analizará este supuesto conflicto, para examinar si determinismo e indeterminismo pueden coexistir de un modo no contradictorio en diferentes estratos de la realidad. Para ello se expondrán los fundamentos de la teoría del caos y de la teoría ergódica. Sobre esta base se podrá formular con precisión el problema del determinismo en sistemas altamente inestables. A partir de ahí se considerarán dos alternativas, en cierto modo complementarias: la primera, en favor de una objetividad estratificada que permite hablar de determinismo e indeterminismo igualmente objetivos, pero relativos al nivel ontológico que se considere en cada caso; la segunda, que interpreta tal dualidad como fundamentalmente epistemológica y reconsidera la relación entre las nociones de determinismo, teoría y sistema real.

1. TEORÍA DEL CAOS Y TEORÍA ERGÓDICA

En el segundo capítulo se han distinguido distintos tipos de determinismos. En este capítulo nuestro interés se centra en el determinismo ontológico: nos preguntaremos acerca del carácter ontológicamente determinista o indeterminista de los sistemas altamente inestables, dejando las cuestiones acerca del determinismo gnoseológico en el ámbito de la predictibilidad. Para ello comenzaremos por brindar ciertas precisiones matemáticas.

El comportamiento temporal de los sistemas dinámicos se describe mediante ecuaciones diferenciales dinámicas, esto es, cuya variable independiente t representa el tiempo. Su solución representa la evolución del sistema, y permite calcular el estado del sistema en un tiempo t en función de su estado en un tiempo inicial t₀ = 0. Podemos representar este comportamiento dinámico en el espacio de las fases, esto es, un espacio geométrico de tantas dimensiones como variables de estado posea el sistema; cada punto representa un posible estado del sistema, y una trayectoria su evolución.

El concepto de estabilidad se refiere al modo en que reacciona un sistema frente a las perturbaciones. Se dice que el estado X_S es estable (estabilidad según Lyapounov)³ si, tras sufrir una perturbación x(t) durante un intervalo Δt, el estado resultante X(t) = X_S + x(t) se mantiene en la vecindad del estado original X_S (Nicolis y Prigogine 1989). Empíricamente, esto significa que la evolución temporal de un sistema es estable si pequeñas modificaciones en las condiciones iniciales dan lugar a pequeñas variaciones en su estado final. Si bien inicialmente el predicado «estable» se aplica a estados, se dice que un sistema es estable cuando todos sus estados posibles son estables. En cambio, los sistemas inestables son aquellos en los cuales algunos o muchos de sus estados son inestables; en este sentido nos referiremos a «sistemas altamente inestables».

La física del siglo XIX estudiaba típicamente situaciones de evolución estable, llegando a creer que todo sistema regido por la mecánica clásica debía poseer esta propiedad. Fueron los trabajos de Henri Poincaré a fines del siglo XIX los que demostraron la existencia de sistemas clásicos que, contra la creencia tradicional, pueden presentar evoluciones temporales inestables. En la actualidad, los sistemas llamados «altamente inestables» se estudian mediante dos enfoques teóricos, la teoría del caos y la teoría ergódica. A continuación presentaremos los elementos básicos de ambos enfoques.

La teoría del caos utiliza para describir los sistemas dinámicos ecuaciones diferenciales ordinarias de primer orden, esto es, que poseen una única variable independiente (el tiempo), y en las que solo intervienen derivadas primeras. Desde el punto de vista empírico, las variables dependientes, o variables de estado, representan las magnitudes físicas que definen el estado del sistema. Cada solución describe la evolución temporal del sistema dadas las condiciones iniciales, esto es, los valores iniciales de las variables de estado. En el espacio de las fases correspondiente al sistema, cada punto representa uno de sus estados posibles y, dado un estado inicial, la evolución temporal del sistema queda representada por una trayectoria que se inicia en dicho punto (véase figura 1).

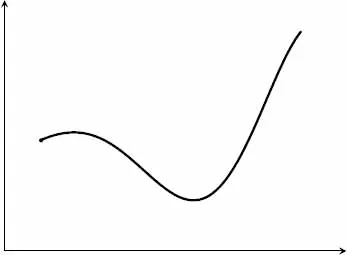
Figura 1. Evolución temporal de un sistema en el espacio de las fases.

Si bien la definición precisa del concepto de caos continúa siendo objeto de debate,⁴ existe un consenso prácticamente unánime entre los especialistas acerca de ciertos aspectos. Los sistemas que pueden presentar comportamiento caótico quedan descritos por sistemas de ecuaciones diferenciales de la forma

dx / dt = F(x, r)

donde x = (x₁, x₂, …, x_d ), F = (F₁, F₂, …, F_d ) y r es un parámetro. Tales ecuaciones son autónomas (F no depende explícitamente de la variable tiempo) y no lineales (F es una función no lineal de las {x_j}).

Todo sistema caótico es sensible a las condiciones iniciales. Esto significa que, en el espacio de las fases correspondiente, las trayectorias divergen exponencialmente. Por ejemplo, supóngase un sistema descrito por un sistema de ecuaciones diferenciales dx / dt = F(x) donde x = (x₁, x₂) y F = (F₁, F₂), y sean dos puntos del espacio de las fases separados inicialmente una distancia δ(0). La distancia entre las trayectorias que se inician en tales puntos debe aumentar exponencialmente con el tiempo según δ(t) = δ(0)e ^ht, donde h se denomina exponente de Lyapounov y mide, precisamente, tal divergencia exponencial (h > 0) (véase figura 2). Por lo tanto, la sensibilidad a las condiciones iniciales que exhiben los sistemas de comportamiento caótico implica su inestabilidad: la evolución temporal del sistema manifiesta grandes variaciones frente a pequeñas modificaciones de las condiciones iniciales.⁵

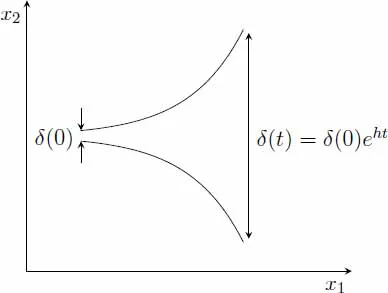
Figura 2. Sensibilidad a las condiciones iniciales de un sistema caótico.

Esta sensibilidad a las condiciones iniciales de los sistemas de comportamiento caótico conduce a una importante consecuencia respecto de la predictibilidad de los estados futuros. La precisión finita de los instrumentos de medición impide conocer con precisión infinita el estado inicial de un sistema. Si se trata de un sistema de comportamiento regular y estable, la situación no es grave: pequeñas incertidumbres en la determinación empírica de las condiciones iniciales se convierten en incertidumbres grandes pero acotadas —aumentan linealmente con el tiempo— en el curso ulterior de la evolución. Pero si el sistema presenta un comportamiento caótico, las pequeñas incertidumbres iniciales se amplifican exponencialmente con el transcurso del tiempo de modo tal que, en la práctica, para tiempos muy superiores a τ = 1/h (tiempo de Lyapounov), la predicción unívoca de los estados futuros del sistema se torna imposible. En otras palabras, a medida que transcurre el tiempo se produce una pérdida de información acerca del microestado preciso en el que se encuentra el sistema; en t = 0 es posible localizar el punto representativo del sistema con una precisión δ; tras un intervalo Δt, su localización en δe^hΔt proporciona una información exponencialmente menor. En meteorología, esta situación se conoce como «efecto mariposa»: la perturbación generada por el batir de las alas de una mariposa podría amplificarse hasta el punto de provocar una tempestad en las antípodas unos días más tarde.⁶

A pesar de esta impredictibilidad, las ecuaciones diferenciales que describen un comportamiento caótico cumplen las condiciones necesarias para asegurar la existencia y la unicidad de sus soluciones para cada conjunto de valores de las variables dependientes:⁷ esto significa que, para cada punto representativo de un estado inicial en el espacio de las fases, la trayectoria que representa la evolución del sistema existe y es única. Dado que no hay restricciones para fijar el estado inicial del sistema, las trayectorias no pueden cortarse en ningún punto, es decir, no existe ningún estado a partir del cual el sistema evolucione temporalmente según dos o más trayectorias posibles. En otras palabras, las evoluciones de un sistema caótico son completamente deterministas (Lombardi 1998, 2001).

La teoría ergódica, por su parte, estudia las propiedades estadísticas de los sistemas dinámicos desde un punto de vista formal (Lebowitz y Penrose 1973). No describe los sistemas en términos de puntos y trayectorias en el espacio de las fases, sino que brinda una descripción mediante una partición de grano grueso: el espacio de las fases Γ se divide en celdas de volumen no nulo, cada una de las cuales representa un estado posible del sistema; cada posible evolución queda así identificada como una sucesión de tales estados (véase figura 3). Sobre esta base, la teoría ergódica permite clasificar los sistemas dinámicos, de acuerdo con su grado creciente de inestabilidad, en sistemas ergódicos, sistemas mezcladores, sistemas K y sistemas Bernoulli. Tales clases no son independientes; cada una de ellas incluye a la siguiente: si un sistema es mezclador, es ergódico, si es de tipo K, es mezclador y ergódico, y así sucesivamente. No se da, en cambio, la implicación inversa.

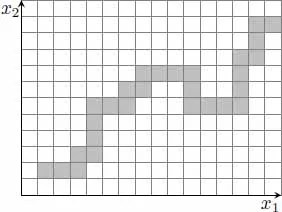
Figura 3. Partición de grano grueso en la teoría ergódica.

La evolución de un sistema descrito por la teoría ergódica posee propiedades estadísticas que fijan la probabilidad asociada a las distintas transiciones posibles entre los estados. En particular, en el caso de los sistemas K, los únicos estados futuros que quedan unívocamente determinados son aquellos que tienen probabilidad 0 o 1 independientemente de la historia del sistema. En otras palabras, las evoluciones en este nivel son indeterministas, puesto que la evolución pasada no fija unívocamente la evolución futura. La teoría ergódica suministra una magnitud que permite precisar las características de este tipo de comportamiento: la K-entropía o entropía de Kolmogorov, que es una medida de la cantidad de estados condicionalmente posibles a partir de la ocurrencia de un estado dado. Si se trata de un sistema K, el valor de la K-entropía es mayor que 0 y es independiente de la particular partición considerada (Farmer 1982). Como muestra la figura 4, la evolución que parte del macroestado inicial se bifurca a partir del quinto estado en dos evoluciones posibles diferentes. A partir de un único estado inicial, la evolución del sistema no queda unívocamente determinada.

Hasta aquí tenemos dos teorías bien fundadas, cada una de ellas con su propio marco teórico. Las dificultades conceptuales comienzan cuando un mismo sistema puede ser descrito adecuadamente por ambas.

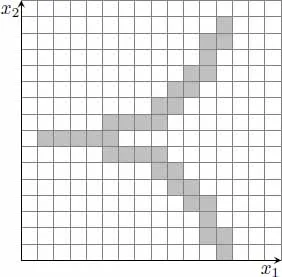
Figura 4. Evolución no determinista de un sistema en la teoría ergódica.

2. EL PROBLEMA DEL DETERMINISMO

El problema del determinismo surge cuando se relacionan las descripciones correspondientes a la teoría del caos y la teoría ergódica en sistemas altamente inestables. Comencemos por distinguir los estados y evoluciones correspondientes a las dos teorías consideradas: nos referiremos al nivel de la teoría del caos como micronivel, y al nivel de la teoría ergódica como macronivel.

El teorema de Pesin demuestra que, cuando un sistema es sensible a las condiciones iniciales en el micronivel —lo cual se manifiesta por la presencia de exponentes de Lyapounov positivos—, tiene K-entropía positiva en el macronivel, y viceversa (Mañé 1987, 265). Por lo tanto, ser un sistema K es condición necesaria y suficiente para el caos: un sistema dinámico es caótico en el micronivel si y solo si en el macronivel resulta ser un sistema K, cuya K-entropía positiva resulta ser proporcional al exponente de Lyapounov (o a la suma de los exponentes de Lyapounov positivos). Esta equivalencia permite caracterizar la alta inestabilidad desde ambas teorías (véase figura 5). No obstante, tal equivalencia no elimina el hecho de que las respectivas propiedades definitorias, divergencia exponencial y K-entropía positiva, son conceptualmente diferentes pues se aplican sobre distintos estados y evoluciones, e incluso conducen a conclusiones opuestas acerca del determinismo.

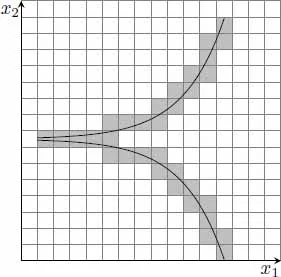
Figura 5. Equivalencia entre los sistemas caóticos (exponentes de Lyapounov positivos) y los sistemas con K-entropía positiva (sistemas k.).

En el micronivel, los sistemas altamente inestables son totalmente deterministas: las evoluciones son unívocas, pero divergen exponencialmente con el tiempo, impidiendo así el conocimiento de los microestados futuros, tras intervalos suficientemente largos, dentro de un margen acotado de error. Pero en el macronivel no entran en juego los errores en la determinación empírica de los microestados ni su evolución exponencialmente divergente: nos hallamos frente a macroevoluciones y probabilidades asociadas a las posibles transiciones entre macroestados. Pero ¿cómo interpretar las propiedades estadísticas de las macroevoluciones? Las opiniones comienzan a distanciarse cuando se trata de decidir acerca de su carácter objetivo o subjetivo.

Muchos autores consideran que la descripción objetiva de los sistemas altamente inestables es la que brindan las ecuaciones diferenciales en el micronivel: puesto que las macroevoluciones son generadas por una evolución determinista subyacente, sus propiedades estadísticas serían subjetivas, debidas a las limitaciones de nuestra capacidad de observación. Como afirma Paul Davies, las propiedades estadísticas de los sistemas altamente inestables se manifiestan «debido a que necesariamente ignoramos los detalles ultrafinos de incluso unos pocos grados de libertad» (Davies 1990, 51). En otras palabras, desde esta perspectiva, los sistemas altamente inestables son deterministas: si conociéramos el microestado pr...

Índice

• Portada
• Resumen
• Página de créditos
• Índice
• Introducción
• Parte Primera. Interrogantes epistemológicos
• Parte Segunda. Interrogantes ontológicos
• Parte Tercera. Interrogantes filosófico-teológicos
• Sobre los autores