Ecuaciones diferenciales

Orlando García Jaimes

• Editorial: Universidad EAFIT
• Año: 2020
• ISBN del libro electrónico: 9789587200645
• Categoría: Matematica
• Categoría: Equazioni differenziali

Ecuaciones diferenciales recoge nuestra experiencia como profesores del curso sobre este tema, y presenta un texto más acorde a las necesidades académicas de los estudiantes. A pesar de la gran cantidad de libros publicados, la mayoría no han sido escritos bajo la óptica de los programas académicos de nuestras universidades. La finalidad primordial es ayudar al estudiante a apropiarse de los conceptos básicos de un curso universitario de Ecuaciones Diferenciales de una manera clara y ágil. Para tal fin se ha presentado la teoría acompañada de gran número de ejercicios resueltos y otros propuestos, con sus respuestas.

Capítulo 1

Ecuaciones diferenciales de primer orden

1.1 Conceptos básicos

Una ecuación diferencial es una ecuación en la que intervienen una función desconocida y una o más de sus derivadas. Si la función tiene śolo una variable independiente, las derivadas serán ordinarias y la ecuación se llama ecuación diferencial ordinaria. Por ejemplo,

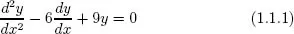
es una ecuación diferencial ordinaria en la que y = y(x) es una función diferenciable de x. Si la función tiene dos o más variables independientes, las derivadas serán parciales y la ecuación en este caso se llama ecuación en derivadas parciales. Por ejemplo,

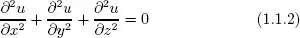
es una ecuación en derivadas parciales, donde u = u(x, y, z) es una función derivable en las variables x, y y z. En este libro estudiamos solamente ecuaciones diferenciales ordinarias.

Además del tipo (ordinarias o parciales), las ecuaciones diferenciales pueden clasificarse por orden y por grado. El orden de la ecuación diferencial es el orden de la más alta derivada que aparece en la ecuación. El grado de una ecuación diferencial es la potencia más alta a la que está elevada la derivada de mayor orden (siempre que la ecuación esté escrita en forma polinómica en cuanto a las derivadas y a la variable dependiente). Por ejemplo, la ecuación 1.1.1 es de orden 2 y grado 1, mientras que la ecuación

y″ − x sen y = 0

es de orden 2, pero no se le asigna grado alguno, ya que el término sen y no se puede escribir en forma polinómica.

Otro concepto importante en el estudio de las ecuaciones diferenciales es el de la linealidad o no linealidad. La ecuación diferencial

F(x, y, y′, . . . , y⁽ⁿ⁾) = 0

se llama lineal si F es una función lineal de las variables y, y′, . . . , y⁽ⁿ⁾. Así, la forma general de una ecuación lineal de orden n puede escribirse como

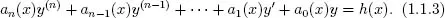
Observe que las ecuaciones diferenciales lineales se caracterizan por lo siguiente:

a) La función y y sus derivadas están elevadas a la potencia 1, es decir, son de primer grado.

b) Cada coeficiente depende de la variable independiente.

Si una ecuación diferencial no cumple lo anterior, se dice que la ecuación es no lineal. Si en la ecuación 1.1.3, h(x) = 0, la ecuación diferencial se llama homogénea; en caso contrario, es no homogénea.

Ejemplo 1.1.1. Clasifique las siguientes ecuaciones diferenciales según su tipo, orden, grado (cuando tenga sentido) y linealidad.

1. y′ + 4y = x³ + 5

2. (y′′′)² − 6y = 3

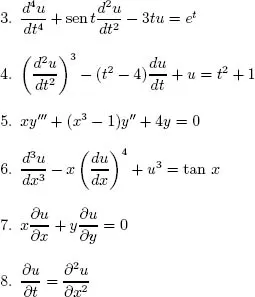
Solución

1. Ordinaria, orden 1, grado 1, lineal

2. Ordinar...

Índice

• Cubierta
• Portada
• Créditos
• Contenido
• Índice de figuras
• Índice de cuadros
• Prólogo
• 1. Ecuaciones diferenciales de primer orden
• 2. Ecuaciones diferenciales de orden superior
• 3. Transformada de Laplace
• 4. Solución de ecuaciones diferenciales mediante series de potencias
• Bibliografía
• Contracubierta