Los números de la vida

Siete principios matemáticos que dan forma a nuestra existencia

Kit Yates, Francisco J. Ramos Mena

• Editorial: Blackie Books
• Año: 2020
• ISBN del libro electrónico: 9788418187513
• Categoría: Matemáticas
• Categoría: Ensayos literarios

 

¿Y si las matemáticas fueran la única forma de comprender cómo te sientes, de entender la sociedad, de intentar articular el mundo?

De encontrar el mejor asiento en el tren y la cola más rápida en la frutería, de calmarte ante un diagnóstico médico inesperado, de aprender del desastre de Chernóbil o del juicio de Amanda Knox, de detener epidemias mortales y víctimas de errores judiciales, de estudiar nuestro pasado para ahorrarnos un futuro peor, de saber cuántos caracoles hay en un jardín. Esto último, preguntado por su hijo, empujó al prestigioso matemático Kit Yates a intentar buscar cómo explicar la magia aplicada de los números que describen nuestra vida y la del planeta.

Todo en este planeta se puede articular mediante las matemáticas y, sin embargo, este no es un libro para matemáticos. Tampoco es un libro de matemáticas al uso. Es un libro sobre cómo nos ayudan a entender el mundo, la sociedad, la vida.

"Yates nos muestra cómo nuestra vida privada y social está empapada de matemáticas. Tan profundamente serio como tremendamente entretenido para los que no sabemos mucho de números. Un libro exquisitamente interesante."
IAN McEWAN 

 "Un narrador deslumbrante. A través de historias y ejemplos increíbles, muestra cómo las matemáticas son el corazón palpitante de la vida moderna. Una voz excitante."   
MARCUS DU SAUTOY  

 "Un libro sobre la confluencia de las matemáticas y las decisiones vitales. Un viaje alucinante sobre las creencias y la verdad." 
THE TIMES  

1

Un estallido silencioso

EL FORMIDABLE PODER Y LOS LÍMITES ALECCIONADORES

DEL COMPORTAMIENTO EXPONENCIAL

Darren Caddick es profesor de autoescuela en Caldicot, un pueblecito de Gales del Sur. En 2009 se le acercó un amigo con una lucrativa oferta. Si invertía 3000 libras en un grupo de inversión local y conseguía que otras dos personas que hicieran lo mismo, obtendría una ganancia de 23000 libras en solo un par de semanas. Al principio, Caddick pensó que era demasiado bueno para ser verdad y resistió la tentación. Pero sus amigos le convencieron de que «nadie saldría perdiendo, porque el plan seguiría y seguiría y seguiría» de manera indefinida, de modo que decidió probar suerte. Lo perdió todo, y diez años después todavía está pagando las consecuencias.

Sin darse cuenta, Caddick se había metido en la base de un esquema piramidal que resultó que no pudo «seguir» indefinidamente. Iniciado en 2008, el esquema —que respondía al nombre de Give and Take («toma y daca»)— se quedó sin nuevos inversores y se desmoronó en menos de un año, pero no sin antes absorber 21 millones de libras de más de 10 000 inversores en todo el Reino Unido, el 90 % de los cuales perdieron su participación inicial de 3000 libras. Los esquemas de inversión que dependen de que sus inversores capten a muchos otros para obtener sus dividendos están condenados al fracaso. El número de nuevos inversores necesarios en cada nivel aumenta en proporción al número de personas ya incorporadas al esquema. En un esquema piramidal de este tipo, tras solo quince rondas de captación de nuevos inversores habría más de 10 000 personas. Aunque esta parece una cifra importante, en el caso de Give and Take se alcanzó con bastante facilidad. Sin embargo, tras otras quince rondas de captación se habría requerido la inversión de uno de cada siete habitantes del planeta para mantener el esquema en marcha. Este vertiginoso tipo de crecimiento, que aquí condujo a una inevitable falta de nuevos inversores y el consecuente desmoronamiento del esquema, se conoce como crecimiento exponencial.

De nada sirve llorar por la leche estropeada

Se dice que algo crece exponencialmente cuando aumenta en proporción a su tamaño actual. Imagina que, cuando abres la botella de leche por la mañana, una sola célula de la bacteria Streptococcus faecalis se cuela en su interior antes de que vuelvas a cerrar el tapón. Strep f. (como se la denomina de forma abreviada) es una de las bacterias que hacen que la leche se agrie y cuaje; pero una célula no parece gran cosa, ¿verdad?¹ Quizá resulta un poco más preocupante descubrir que, una vez en la leche, una célula de Strep f. puede dividirse y producir dos células hijas cada hora.² En cada generación, el número de células aumenta en proporción al número actual de estas, de modo que su número crece exponencialmente.

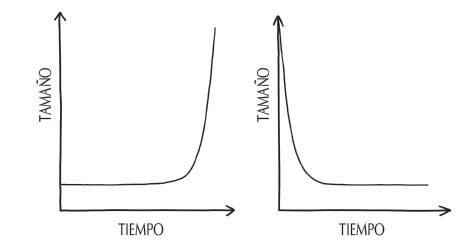
La curva que describe cómo aumenta una cantidad que crece exponencialmente tiene una forma que recuerda a una de las típicas rampas que utilizan los aficionados a hacer piruetas con patines, monopatines o bicicletas BMX. Inicialmente, la pendiente de la rampa es muy suave: la curva es extremadamente poco pronunciada, y solo va ganando altura de una forma muy gradual (como puedes ver en la primera curva de la Figura 2). Al cabo de dos horas hay cuatro células de Strep f. en la leche, y al cabo de cuatro todavía hay solo 16, lo que no parece que represente un gran problema. Sin embargo, al igual que ocurre con la mencionada rampa, luego la altura y la inclinación de la curva exponencial aumentan con rapidez. Al principio, las cantidades que crecen exponencialmente pueden dar la impresión de que aumentan poco a poco, pero de repente despegan de una forma que parece tan abrupta como inesperada. Si te olvidas de la leche durante cuarenta y ocho horas, y el crecimiento exponencial de las células de Strep f. se mantiene, la próxima vez que vuelvas a verterla en tus cereales podría haber casi 1000 billones de células en la botella; suficientes para hacer que se te cuaje la sangre, y no digamos ya la leche. En este punto, las células superarían en número al total de habitantes de nuestro planeta en una proporción de 40 000 a uno. A veces se alude a las curvas exponenciales como «curva en forma de J», ya que su forma se asemeja mucho a la curva pronunciada característica de dicha letra. Obviamente, a medida que las bacterias consumen los nutrientes de la leche y cambian su pH las condiciones de crecimiento se van deteriorando, de manera que el incremento exponencial solo se mantiene durante un período de tiempo relativamente breve. De hecho, en casi todos los escenarios del mundo real el crecimiento exponencial a largo plazo resulta insostenible, y en muchos casos patológico, dado que el sujeto en crecimiento consume recursos de manera inviable. Así, por ejemplo, el crecimiento exponencial sostenido de las células del cuerpo es un rasgo distintivo del cáncer.

Figura 2. Curvas «en forma de J» de crecimiento exponencial (izquierda) y decaimiento exponencial (derecha).

Otro ejemplo de curva exponencial es un tobogán acuático de caída libre, llamado así porque inicialmente el tobogán es tan empinado que el usuario experimenta la sensación de estar en caída libre. Pero en este caso, al proseguir nuestro avance por el tobogán, nos deslizamos por una curva de decaimiento exponencial, en lugar de una curva de crecimiento (puedes ver un ejemplo en la segunda imagen de la Figura 2). Se produce decaimiento exponencial cuando una cantidad disminuye en proporción a su tamaño actual. Imagina que abres una enorme bolsa de M&M’s, los viertes sobre la mesa y empiezas a comer todos los que han caído con el lado que lleva la letra M hacia arriba. Guarda el resto de la bolsa para mañana. Al día siguiente, agita la bolsa y vierte nuevamente los M&M’s; de nuevo, cómete los que tienen la letra M a la vista y guarda el resto en la bolsa. Cada vez que viertas los caramelos de la bolsa te comerás aproximadamente la mitad de los que quedan, independientemente de la cantidad con la que empezaste en un primer momento. El número de caramelos disminuye en proporción a los que quedan en la bolsa, lo que se traduce en una disminución exponencial de la cantidad de caramelos. De manera similar, el tobogán acuático exponencial empieza siendo vertical en la parte de arriba, de manera que la altura a la que está el usuario disminuye muy deprisa, al igual que, cuando tenemos un gran número de caramelos, la cantidad que nos comemos también es grande. Pero la curva se va haciendo más gradual y cada vez menos empinada hasta que llega a ser casi horizontal al final del tobogán; del mismo modo, cuantos menos caramelos dejemos, menos podremos comer al día siguiente. Aunque el hecho de que un caramelo individual aterrice en la mesa con la M hacia arriba o hacia abajo es aleatorio e imprevisible, la curva predecible del decaimiento exponencial, en forma de tobogán acuático, es el resultado del número de caramelos que vamos dejando a lo largo del tiempo.

A lo largo de este capítulo descubriremos los vínculos ocultos que existen entre el comportamiento exponencial y diversos fenómenos cotidianos: la propagación de una enfermedad en una población o de un meme en Internet; el rápido crecimiento de un embrión o el crecimiento demasiado lento del dinero de nuestra cuenta bancaria; la forma en que percibimos el tiempo, y hasta la explosión de una bomba nuclear. En nuestro avance iremos desentrañando meticulosamente toda la tragedia del esquema piramidal Give and Take. Las historias de las personas que vieron cómo su dinero era succionado y tragado servirán para ilustrar lo importante que resulta ser capaces de pensar en términos exponenciales, lo que por otro lado nos ayudará a anticipar el ritmo de cambio, a veces sorprendente, del mundo moderno.

Un asunto de gran interés

En las contadísimas ocasiones en que hago un depósito en mi cuenta bancaria, me consuela el hecho de que, por poco que tenga en ella, siempre está creciendo exponencialmente. De hecho, una cuenta bancaria es uno de los lugares donde realmente no hay límites al crecimiento exponencial, al menos sobre el papel. Siempre que el interés sea compuesto (es decir, que el interés se añada a nuestra cantidad inicial y genere nuevo interés por sí mismo), la cantidad total depositada en la cuenta aumenta en proporción a su tamaño actual, lo que, como hemos visto, constituye el rasgo distintivo del crecimiento exponencial. En palabras de Benjamin Franklin: «El dinero gana dinero, y el dinero que gana el dinero gana más dinero». Si pudiéramos aguardar lo bastante, hasta la inversión más pequeña se convertiría en una fortuna. Pero no vayas corriendo aún a cerrar tu fondo para contingencias. Si invirtieras 100 euros al 1 % anual, tardarías más de 900 años en hacerte millonario. Aunque suele asociarse a incrementos rápidos, si la tasa de crecimiento y la inversión inicial son pequeñas, el crecimiento exponencial puede resultar de hecho muy lento.

La otra cara de la moneda es que, dado que se cobra un tipo de interés fijo sobre el monto pendiente (a menudo un tipo alto), las deudas de las tarjetas de crédito también pueden crecer exponencialmente. Al igual que ocurre con las hipotecas, cuanto antes amortices tus tarjetas de crédito y más pagues desde el principio, acabarás pagando menos en conjunto, ya que el crecimiento exponencial nunca tendrá la oportunidad de despegar.

La posibilidad de amortizar las hipotecas y saldar otras deudas fue una de las principales razones esgrimidas por las víctimas de Give and Take para involucrarse de entrada en el esquema. La tentación de conseguir dinero rápido y fácil para reducir las presiones financieras resultó demasiado difícil de resistir para muchos, pese a la persistente sospecha de que algo no acababa de encajar. Como admite el propio Caddick, «la vieja máxima de que “si algo parece demasiado bueno para ser verdad, probablemente lo es”, resulta muy, muy acertada en este caso».

Las personas que pusieron en marcha el esquema, las jubiladas Laura Fox y Carol Chalmers, eran amigas desde la época en la que estudiaron en un colegio de monjas católico. Ambas tenían un cierto peso en su comunidad local —una ejercía como vicepresidenta de la filial del club Rotary de su localidad, mientras que la otra era una abuela muy respetada—, y sabían exactamente lo que hacían cuando crearon su fraudulento plan de inversión. Give and Take fue ingeniosamente diseñado para engatusar a posibles inversores al tiempo que ocultaba sus peligros. A diferencia del tradicional esquema piramidal de dos niveles, en el que la persona que ocupa la parte superior de la cadena cobra directamente de los inversores que ha captado y que tiene inmediatamente «debajo», Give and Take operaba como un esquema basado en cuatro niveles. Este sistema recibe nombres distintos en diferentes países; en Norteamérica se conoce como «el juego del avión». En un esquema tipo «avión», la persona de la parte superior de la cadena es el «piloto». Este capta a dos «copilotos», cada uno de los cuales capta a su vez a dos «miembros de la tripulación», cada uno de los cuales capta a dos «pasajeros». En el esquema de Fox y Chalmers, una vez completada esta jerarquía de 15 personas, los ocho pasajeros pagaban sus 3000 libras a las organizadoras, que a su vez ofrecían un enorme beneficio de 23 000 libras al inversor inicial, cobrándose una comisión de 1000. Parte de este dinero se donaba a organizaciones benéficas, y las cartas de agradecimiento remitidas por estas (por ejemplo, la NSPCC, la Sociedad Nacional para la Prevención de la Crueldad con los Niños) añadían legitimidad al esquema; las organizadoras también destinaban otra parte a garantizar el funcionamiento fluido y constante del plan.

Tras cobrar sus beneficios, el piloto abandona el esquema y sus dos copilotos son ascendidos al rango de pilotos, aguardando a la captación de ocho nuevos pasajeros en la base de su pirámide. Los esquemas tipo avión resultan especialmente atractivos para los inversores, ya que cada nuevo participante solo necesita captar a otras dos personas para multiplicar por ocho su inversión (aunque, por supuesto, luego cada una de ellas tiene que captar a otras dos, y así sucesivamente). Otros esquemas, más planos, requieren un esfuerzo de captación individual mucho mayor para obtener los mismos rendimientos. Por otra parte, la estructura de cuatro niveles de Give and Take implicaba que los miembros de la tripulación nunca cobraban directamente de los pasajeros que captaban. Dado que es probable que las nuevas personas captadas sean amigas y parientes de los miembros de la tripulación, esto garantiza que el dinero nunca se transmita directamente entre personas con una estrecha relación. Esta separación entre los pasajeros y los pilotos cuyos pagos financian hace que la captación resulte más fácil y que disminuya la probabilidad de represalias, lo que genera una oportunidad de inversión más atractiva y, por ende, facilita la captación de miles de inversores en el esquema.

Del mismo modo, muchos de los inversores del esquema piramidal Give and Take obtuvieron la confianza necesaria para invertir tras enterarse de casos de personas que habían invertido con anterioridad y habían cobrado sus beneficios, y, en algunas ocasiones, incluso de haber presenciado personalmente el cobro. Con este fin, las organizadoras del esquema, Fox y Chalmers, organizaban lujosas fiestas privadas en el hotel Somerset, propiedad de esta última. En los folletos que se repartían en dichas fiestas se incluían fotos de los miembros del esquema tend...

Índice

• Portada
• Los números de la vida
• Créditos
• Introducción: Casi todo
• 1. Pensar exponencialmente: El formidable poder y los límites aleccionadores del comportamiento expo
• 2. Sensibilidad, especificidad y segunda opinión: Por qué las matemáticas realzan la medicina
• 3. Las leyes de las matemáticas: El papel de las matemáticas en la ley
• 4. No te creas la verdad: Cómo desacreditar las estadísticas que nos presentan los medios
• 5. Lugar equivocado, momento equivocado: La evolución de nuestros sistemas numéricos y cómo nos defr
• 6. Optimización implacable: El ilimitado potencial de los algoritmos, desde la evolución hasta el co
• 7. Susceptible, infeccioso, eliminado: Contener la enfermedad está en nuestras manos
• Epílogo: Emancipación matemática
• Agradecimientos
• Notas