Geometría para diseño gráfico

Carlos Rojas Álvarez

• Editorial: Universidad del Norte
• Año: 2017
• ISBN del libro electrónico: 9789587419436
• Edición: 1
• Categoría: Mathematics
• Categoría: Geometry

Este texto está dirigido a estudiantes de Diseño Gráfico, Arquitectura, Artes y básica secundaria. Su propósito es aplicar la geometría a algunas situaciones relacionadas con el diseño, tales como las vistas de un sólido, la proporción y el número áureo, sin perder la rigurosidad de los conceptos y propiedades de la geometría elemental.

Unidad 1

PROYECCIONES

1.1. Conceptos básicos

1.2. Proyección de vista múltiple

1.3. Proyección isométrica

Referencias

RESEÑA HISTÓRICA

Gaspar Monge (1746-1818). Matemático francés que se destacó por enlazar la ciencia teórica con diversas aplicaciones. Los métodos de la geometría descriptiva se basan en la comprensión del concepto de proyección ortogonal y del conocimiento de la relación entre las dos proyecciones ortogonales de la misma figura. Monge clarificó definitivamente los principios de conjunto que permiten construir la geometría descriptiva a partir de una técnica gráfica, así como desarrollar sus métodos y sugerir aplicaciones, razón por la que se le considera el creador de este tipo de geometría. Uno de sus libros, Geometría descriptiva, es la recopilación de las sesiones de las escuelas normales que realizó como profesor, y fue editado por primera vez en 1799, y por cuarta vez en 1820.

1.1. CONCEPTOS BÁSICOS

DEFINICIÓN 1.1.1

Una recta y un plano son perpendiculares si y solo si: 1) se intersecan; y 2) toda recta en el plano que pase por el punto de intersección es perpendicular a la recta dada.

Cuando la recta l y el plano K son perpendiculares, lo denotamos por l ⊥ K o K ⊥ l. Si P es el punto de intersección, entonces escribimos que l ⊥ K en P.

DEFINICIÓN 1.1.2

La distancia a un plano desde un punto que no está situado en él, es la longitud del segmento perpendicular desde el punto al plano.

PROPIEDAD 1.1.1 (EL SEGUNDO TEOREMA DE LA MÍNIMA DISTANCIA)

El segmento más corto desde un punto a un plano que no lo contiene es el segmento perpendicular.

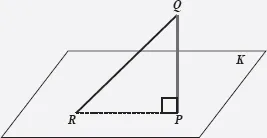
Figura 96. La distancia más corta del punto Q al plano K es la distancia PQ.

DEFINICIÓN 1.1.3

Dos planos, o un plano y una recta, son paralelos, si y solo si no se intersecan. Si los planos K y J son paralelos, escribimos K ‖ J. Si la recta l y el plano K son paralelos, escribimos K ‖ J o J ‖ K.

El paralelismo en el espacio se comporta de manera parecida al paralelismo en el plano. Sin embargo, hay diferencias. Una de ellas es que no hay planos alabeados. Cada dos planos en el espacio o se intersecan, o son paralelos. Además, si dos rectas están en planos paralelos, no se puede deducir que las rectas sean paralelas, como lo muestra la representación de la izquierda de la figura 97. También, si dos rectas son paralelas, siempre podemos encontrar dos planos que las contienen y que no son paralelos, como lo muestra la representación de la derecha de la figura 97.

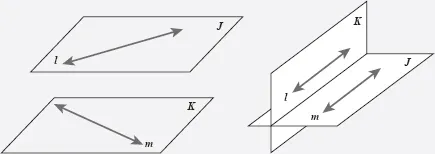
Figura 97.

PROPIEDAD 1.1.2

Dos rectas paralelas al mismo plano son paralelas.

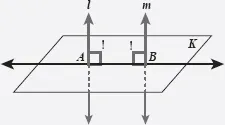
Figura 98. Si l ⊥ K en A, y m ⊥ K en B, entonces l ‖ m.

PROPIEDAD 1.1.3

Dos planos paralelos equidistan en toda su extensión.

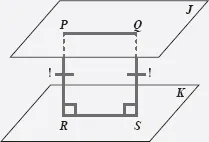
Figura 99. Si J ‖ K, entonces todos los puntos de J equidistan de K.

DEFINICIÓN 1.1.4

La proyección de un punto sobre un plano es el pie de la perpendicular que va del punto al plano.

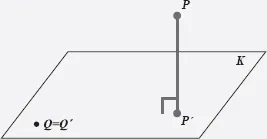
Figura 100. P’ es la proyección del punto P sobre el plano K. Se admite la posibilidad de que el punto Q esté en K, en cuyo caso la proyección d...

Índice

• Cubierta
• Portadilla
• Página legal
• Contenido
• INTRODUCCIÓN
• CONCEPTOS PRELIMINARES
• Unidad 1: PROYECCIONES
• Unidad 2: PROPORCIONES
• ANEXOS
• Cubierta posterior