Los superconductores

Luis Fernando Magaña

• Editorial: Fondo de Cultura Económica
• Año: 2013
• ISBN del libro electrónico: 9786071613707
• Categoría: Ciencias físicas
• Categoría: Física

El propósito de esta obra es ofrecer un breve resumen de las investigaciones alrededor de los superconductores, desde su historia hasta sus posibles aplicaciones. De esta forma, en el primer capítulo se ocupa de su descubrimiento; en los tres capítulos siguientes describe las propiedades de los superconductores tipo I, tipo II y los exóticos o atípicos; en el quinto, hace hincapié en las aplicaciones de la superconductividad; finalmente, en el sexto, hace una revisión de todo el libro a través de imágenes, y en el séptimo incluye la biografía de los ganadores del Premio Nobel de física relacionados con la superconductividad.

II. Los superconductores ideales o tipo I

EL CAMPO MAGNÉTICO CRÍTICO

También correspondió a Heike Kamerlingh Onnes observar que a cualquier temperatura T, tal que T < T_c, el estado superconductor podía ser destruido por la aplicación de un campo magnético con intensidad mayor que un cierto campo magnético crítico. Por otro lado, también notó que a cualquier temperatura T < T_c, en ausencia de un campo magnético, el estado superconductor podía destruirse aumentando la corriente por arriba de un valor crítico y, asimismo, que la temperatura de transición superconductora (T_c) disminuía cuando la corriente que pasaba por el superconductor crecía. Los efectos de las corrientes eléctricas y de los campos magnéticos sobre el estado superconductor no son ajenos entre sí, ya que la disminución del valor de T_c, con el aumento de la corriente, se debe al campo magnético que la corriente produce.

Experimentalmente se encuentra que el valor del campo crítico depende de la temperatura, cayendo de un valor H₀, a temperaturas muy bajas, hasta un valor de cero para la temperatura de transición T_c. Los datos experimentales revelan que la variación del campo crítico con la temperatura queda bastante bien descrita (dentro de 2 o 3% de margen de error) por una parábola de la forma:

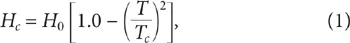
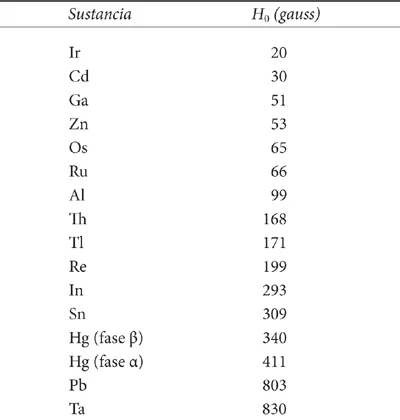
CUADRO II.1

donde H_c es el campo magnético crítico y H₀ es el campo crítico extrapolado al cero absoluto. Cada material puede ser caracterizado por sus valores de T_c y de H₀ y, conociendo éstos, se puede utilizar la ecuación (1) para encontrar el campo crítico a cualquier temperatura.

Es de hacer notar que las curvas experimentales de la variación del campo crítico con la temperatura no son exactamente parábolas, y para describirlas de una manera más precisa que la ya señalada se requeriría un polinomio en potencias de la temperatura, que en general es de grado diferente de 2. Para la mayoría de los cálculos es suficiente con utilizar la ecuación (1).

El cuadro II.1 muestra los valores del campo crítico de algunas sustancias para el valor extrapolado a T = 0 K.

LA ENERGÍA DE LA TRANSICIÓN

Hemos visto en el capítulo anterior que, en virtud del efecto Meissner-Oschenfeld, el estado de magnetización de un material en el estado superconductor depende sólo de la temperatura de la muestra y del campo magnético aplicado, y no de la manera en que se llega a esos valores. Es posible, por tanto, aplicar argumentos termodinámicos al estudio del comportamiento de un material en el estado superconductor utilizando como variables la temperatura y el campo magnético.

Sabemos que para comprimir un gas en el interior de un cilindro a presión constante tenemos que realizar un trabajo ΔW = PΔV, donde P es la presión y Δ V es el cambio en el volumen del gas contenido en el cilindro. Del mismo modo, cuando aplicamos un campo magnético a una muestra el trabajo realizado por unidad de volumen de la muestra es ΔW = −H dM, el signo menos sólo indica que cuando la magnetización aumenta (dM > 0) el trabajo se está realizando sobre el sistema.

Con lo anterior, se puede encontrar fácilmente el cambio en la energía libre del material al pasar de un estado a otro. Este cambio está dado por el trabajo realizado mediante el campo magnético aplicado a la muestra. Se encuentra que la cantidad requerida de energía, a temperatura constante, para destruir el estado superconductor y cuando en el estado inicial existe un campo magnético aplicado, es:

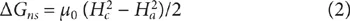
En la ecuación (2), μ₀ es una constante que vale 4π × 10⁻⁷ henry/metro y es la constante de permeabilidad magnética del vacío; H_c es el campo magnético crítico para una temperatura dada y ΔG_ns es el cambio en la energía de la muestra al pasar del estado superconductor al estado normal, por medio de la aplicación de un campo magnético.

Si inicialmente el campo magnético aplicado es cero, H_c = 0, y la ecuación (2) nos da, para este caso, la energía total requerida para destruir el estado superconductor, tendremos que, por unidad de volumen, la diferencia de energía entre el estado normal y el estado superconductor es μ₀H_c (T)²/2. Para tener una idea de la magnitud de la energía, hallemos su valor para el plomo y el aluminio. Si suponemos T = 0, para plomo, H_c(0) = 803 gauss y

ΔG_ns = 2.5 × 10⁴ erg/cm³ = 1.6 × 10¹⁶ ev/cm³.

Es muy ilustrativo pasar esta energía a ev/átomo, para comparar con las energías típicas de las partículas en el material. Tenemos que hallar el número de partículas de plomo en 1 cm³. Para esto, recordemos que 1 mole de Pb tiene 207 gr y que la densidad del plomo es de 11.4 gr/cm³. Por otro lado, el número de Avogadro es 6.03 × 10²³ átomos/mole. Con estos datos encontramos que en 1 mole de plomo hay 3 × 10²² átomos aproximadamente. De aquí que:

ΔG_ns = 5 × 10⁻⁷ ev/átomo.

Ahora bien, la energía típica de un electrón en el interior de un metal se puede tomar como la energía de Fermi para ese metal. Para Pb es de aproximadamente 5 ev.

Por otro lado, la energía típica de un ion en el material se puede tomar como K_B Θ_D, donde K_B es la constante de Boltzmann y Θ_D es una constante típica del material que se llama la temperatura de Debye.

Para Pb la energía típica de un ion resulta ser de 10 ev.

De lo anterior podemos darnos cuenta que la energía involucrada en la transición superconductora es mucho menor que la energía típica de una partícula en el metal.

Veamos ahora el caso del aluminio. Para este metal la energía de transición al estado superconductor es de 1.4 × 10⁻⁹ ev/átomo. La energía de Fermi para aluminio es de 1 ev aproximadamente y la energía típica de un ion resulta ser de 5.91 × 10⁻² ev/átomo. Nuevamente vemos que la energía de transición al estado superconductor, por partícula, resulta ser mucho menor que las energías típicas de las partículas en el metal. La magnitud de la energía para la transición al estado superconductor fue una de las pautas para el establecimiento de una teoría microscópica de la superconductividad.

EL DESORDEN

Sabemos, a partir de la termodinámica, que una medida del orden o del desorden en un sistema la da el valor de la entropía. Si un sistema en un estado dado tiene un valor para la entropía mayor que el valor para el mismo sistema en otro estado, se dice que el segundo estado es más ordenado que el primero. De este modo, si los iones de un metal presentan un arreglo periódico, este estado tendrá menor entropía (y por tanto mayor orden) que el metal en estado líquido.

Una de las primeras preguntas que surgieron cuando se descubrió la superconductividad fue si el estado superconductor es más ordenado (o desordenado) que el estado normal; se puede responder estimando el cambio en la entropía del material al pasar del estado normal al estado superconductor. Haciendo unos cálculos termodinámicos sencillos se puede demostrar que el cambio en el valor de la entropía por unidad de volumen al pasar del estado superconductor al estado normal, ΔS_ns, está dado por:

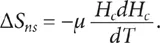
Ahora bien, podemos hacer uso de la expresión de la variación del campo magnético crítico en función de la temperatura para hallar dH_c/dT, ecuación (1), y obtenemos que:

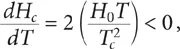
y por tanto, ΔS_ns > 0, lo cual significa que la entropía en el estado superconductor es menor que la entropía en el estado normal. En otras palabras, que el estado superconductor es más ordenado que el estado normal del material. Sin embargo, ya vimos anteriormente que una de las propiedades del material que no cambian al pasar al estado superconductor es la estructura cristalina, lo que significa que el mayor ordenamiento que se presenta en el material al pasar al estado superconductor no se debe a un mayor ordenamiento de la red cristalina, ya que ésta no sufre cambio alguno. El ordenamiento tiene que ser de la otra propiedad del material, de la parte que corresponde a los electrones. Podemos esperar que los electrones lleguen a un estado de mayor ordenamiento del que tienen en estado normal. Este hecho también dio una pauta para el establecimiento de una teoría microscópica de la superconductividad.

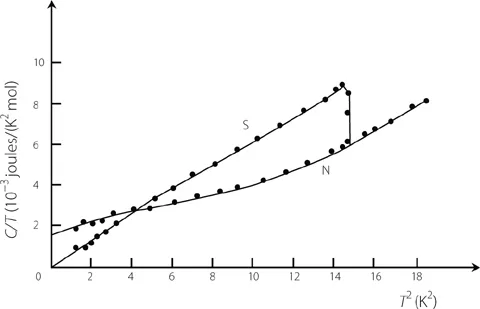
FIGURA II.1. Variación del calor específico del estaño. El campo magnético aplicado es cero para el caso superconductor, S. El campo magnético aplicado es mayor que el campo magnético crítico para el caso normal, N, como función de la temperatura. Nótese el salto en el valor del calor específico.

EL CALOR ESPECÍFICO

Al igual que en un metal en el estado normal, el calor específico de un metal en el estado superconductor consiste, básicamente, en una contribución de la red de iones del metal (o red cristalina), C_r, y una contribución electrónica, C_el. De este modo, si C es el calor específico de un metal en el estado normal: C = C_r + C_el. A bajas temperaturas se tiene que C_el = γT, donde γ es una constante para cada material, T es la temperatura medida en kelvin y C_r = A (T/Θ_D)³, donde A es una constante numérica para todos los metales y Θ_D es la temperatura de Debye.

Experimentalmente se encuentra que la contribución electrónica al calor específico en el estado superconductor está dada por:

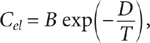
donde B y D son constantes del material.

Esta variación exponencial de la contribución electrónica al calor específico es radicalmente distinta de la correspondiente en el estado normal y también, por cierto, típica de la contribución electrónica al calor específico de un material semiconductor. Ésta era otra indicación de que algo extraordinario estaba ocurriendo con los electrones al pasar el material al estado superconductor. Esta variación del calor específico, en su parte correspondiente a los electrones, también sentó una importante pauta para el establecimiento de una teoría microscópica de la superconductividad.

LOS IONES Y LA TRANSICIÓN

Una indicación de que los iones del metal influyen de alguna manera en el cambio de comportamiento de los electrones al pasar al estado superconductor la dio el que fue llamado efecto isotópico. Para entenderlo, recordemos que un isótopo es una variedad de un elemento químico que, teniendo el mismo número de protones en el núcleo atómico, difiere de...

Índice

• Portada
• Índice
• Agradecimientos
• Prólogo a la segunda edición
• Prólogo a la primera edición
• Prefacio
• I. Qué es la superconductividad
• II. Los superconductores ideales o tipo I
• III. Los superconductores duros o tipo II
• IV. Los llamados superconductores exóticos o atípicos
• V. Algunas aplicaciones de la superconductividad
• VI. La superconductividad en imágenes
• VII. Premios Nobel de Física relacionados con la superconductividad
• Bibliografía recomendada