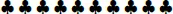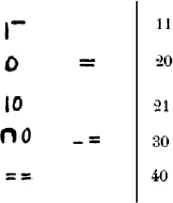Aprender Matemática significa construir conceptos, estudiar sus propiedades y sus interacciones con otros conceptos. Este libro invita a sus lectores, estudiantes y profesores, a aprender un concepto especifico, el de pensamiento recursivo. Para ello se propone comenzar mostrando de qué modo la recursividad está enraizada en la actividad cotidiana que llamamos 'contar'. Luego de exponer cómo se manifestaba la recursividad en los sistemas numéricos fenicios, babilónicos y mayas, se pasa a estudiar la aritmética pitagórica tal y como la transmitió Boecio. Se construyen recursivamente los números figurados: triangulares, rectangulares, cuadrados, pentagonales, hexagonales. Se estudian relaciones entre ellos de manera de adentrar a los lectores en lo que llamamos una demostración matemática. La recursividad se estudia luego en el 'Triangulus Arithmeticus' de Pascal: se ofrece una de sus primeras traducciones al español, la que se complementa con comentarios que relacionan el triángulo de Pascal con los números figurados y los números combinatoriales. Subyacen al libro las ideas básicas del intuicionismo matemático del filósofo y matemático holandés Luitzen Brouwer y las contribuciones sobre la lógica dialogal desarrolladas por el matemático y filósofo alemán Paul Lorenzen.
Preguntas frecuentes
Sí, puedes cancelar tu suscripción en cualquier momento desde la pestaña Suscripción en los ajustes de tu cuenta en el sitio web de Perlego. La suscripción seguirá activa hasta que finalice el periodo de facturación actual. Descubre cómo cancelar tu suscripción.
Por el momento, todos los libros ePub adaptables a dispositivos móviles se pueden descargar a través de la aplicación. La mayor parte de nuestros PDF también se puede descargar y ya estamos trabajando para que el resto también sea descargable. Obtén más información aquí.
Perlego ofrece dos planes: Esencial y Avanzado
Esencial es ideal para estudiantes y profesionales que disfrutan explorando una amplia variedad de materias. Accede a la Biblioteca Esencial con más de 800.000 títulos de confianza y best-sellers en negocios, crecimiento personal y humanidades. Incluye lectura ilimitada y voz estándar de lectura en voz alta.
Avanzado: Perfecto para estudiantes avanzados e investigadores que necesitan acceso completo e ilimitado. Desbloquea más de 1,4 millones de libros en cientos de materias, incluidos títulos académicos y especializados. El plan Avanzado también incluye funciones avanzadas como Premium Read Aloud y Research Assistant.
Ambos planes están disponibles con ciclos de facturación mensual, cada cuatro meses o anual.
Somos un servicio de suscripción de libros de texto en línea que te permite acceder a toda una biblioteca en línea por menos de lo que cuesta un libro al mes. Con más de un millón de libros sobre más de 1000 categorías, ¡tenemos todo lo que necesitas! Obtén más información aquí.
Busca el símbolo de lectura en voz alta en tu próximo libro para ver si puedes escucharlo. La herramienta de lectura en voz alta lee el texto en voz alta por ti, resaltando el texto a medida que se lee. Puedes pausarla, acelerarla y ralentizarla. Obtén más información aquí.
¡Sí! Puedes usar la app de Perlego tanto en dispositivos iOS como Android para leer en cualquier momento, en cualquier lugar, incluso sin conexión. Perfecto para desplazamientos o cuando estás en movimiento. Ten en cuenta que no podemos dar soporte a dispositivos con iOS 13 o Android 7 o versiones anteriores. Aprende más sobre el uso de la app.
Sí, puedes acceder a Aritmética pitagórica y el triángulo de Pascal de Ernesto San Martín en formato PDF o ePUB, así como a otros libros populares de Pedagogía y Enseñanza de matemáticas. Tenemos más de un millón de libros disponibles en nuestro catálogo para que explores.
Todo está formado a partir de la naturaleza del Mismo y de la naturaleza del Otro; esto se ve primeramente en los números.
BOECIO, Instituciones Aritméticas, LIBRO II, N° 33.
2.1. Secuencia de signos: una actividad milenaria
Comencemos recordando las palabras de Brouwer mencionadas en el capítulo anterior:
“Uno, dos, tres, ...”, conocemos de memoria la secuencia de estos sonidos como una fila sin fin, es decir, que continúa por siempre de acuerdo a una ley que se sabe es fija.
Al lado de esta secuencia de sonidos-imágenes poseemos otra secuencia que procede de acuerdo a una ley fija, por ejemplo, la secuencia de los signos escritos 1, 2, 3...
Estas cosas son intuitivamente claras.
Uno de los elementos que queremos subrayar es el que dice relación con la representación de los números naturales como una fila sin fin de signos. Vamos a mostrar que esta no es una idea reciente, sino que más bien se trata de una actividad milenaria desarrollada por la humanidad que denominamos contar.
2.1.1. ¿Qué hacemos cuando contamos?
La pregunta básica con la que podemos comenzar nuestro aprendizaje de la aritmética constructivista es la siguiente:
¿Qué significa contar? ¿Qué actividades se realizan cuando contamos?
Contar es una de las actividad más antiguas que el ser humano ha desarrollado. Es tan cercana a nosotros, que probablemente tengamos algunas dificultades para convencernos de la importancia de estas preguntas. Pero hagamos un esfuerzo, pidiendo a nuestros estudiantes que cuenten las sillas de la sala, las mesas, a sus compañeros, etc.
Por ejemplo, contemos este grupo de tréboles:
Cualquiera de nosotros hará esto: uno, dos, tres, cuatro, cinco, seis, siete, ocho y dirá: hay ocho tréboles. Cuando contó los tréboles, ¿qué hizo? Cuando contó el primer trébol dijo: uno. Cuando dijo dos, ¿qué estaba haciendo? Formula estas preguntas a tus alumnos -y a ti mismo- tratando de percibir cuál de las siguientes dos actividades realizas(n) cuando cuentas(n) el segundo trébol: ¿asignan el dos al segundo trébol, o asignan el dos a los dos primeros tréboles? La primera actividad se puede ilustrar por medio de la figura 2.1. Sin embargo, esta actividad no refleja la significación que damos a los signos 1, 2, 3, 4, 5, 6, 7 y 8.
Figura 2.1: Contando 8 tréboles: primera representación
¿Cómo representamos figurativamente lo que hacemos cuando contamos los 8 tréboles? ¡La respuesta debe salir de tus alumnos! La figura 2.2 es una posible representación.
Cuando contamos, formamos una secuencia de signos. Esta secuencia está normada por una regla: ¿cuál es esa regla? La respuesta la podemos extraer observando atentamente la figura 2.2:
1. Partimos con un signo inicial:
.
Figura 2.2: Contando 8 tréboles: segunda representación
2. Luego, al signo inicial le añadimos un
, obteniendo así
.
3. Luego, al signo obtenido le añadimos un
, obteniendo así
.
4. Luego, al signo obtenido le añadimos un
, obteniendo así
.
5. Y así sucesivamente.
Pero también hacemos otra actividad cuando contamos: ¿cuál es? Nuevamente, si observamos la figura 2.2 podremos formular una respuesta: introducimos nuevos signos, el 1, 2, 3... ¿por qué los introducimos? Responder a esta pregunta significa entender el poder que tiene la escritura simbólica. Los signos numéricos 1, 2, 3, 4... han sido introducidos para abreviar concatenaciones de signos. Así, es más simple escribir 10 que escribir
Podemos concluir que los signos 1, 2, 3... nos ayudan a simplificar nuestros procedimientos de conteo. Este procedimiento de simplificación sin duda que lo podemos entender como un procedimiento de eficiencia: es más eficiente escribir 25 que representar 25 tréboles de la siguiente manera:
Pero ¡cuidado! No solo hay eficiencia aquí, sino que hay una actividad que es propia de los seres humanos: ¿sabes cuál es? Es tan importante esta pregunta que la dejamos enmarcada:
Cuando un niño, un adulto o un anciano utilizan los signos 1, 2, 3... mientras cuentan, ¿qué actividad propia de los seres humanos están realizando?
Responder a esta pregunta no solo significa dar un paso más en nuestro aprendizaje constructivo de la aritmética, sino además valorar los enormes procesos de aprendizaje que tus estudiantes realizan toda vez que cuentan. Para responder a esta pregunta, sigamos hablando de las secuencias de signos.
2.1.2. El sistema numérico fenicio
El procedimiento que hemos descrito no es nuevo, sino que pertenece a nuestra herencia cultural. La actividad de concatenación simbólica puede rastrearse en las representaciones numéricas utilizadas por los fenicios hacia el 3000 a. C. La figura 2.3 muestra cómo los primeros diez números naturales eran concebidos como concatenaciones de un signo-unidad, a saber, una barra.
Figura 2.3: Los primeros diez numerales fenicios
Los primeros nueve números naturales se obtienen de la misma forma que hemos descrito en la figura 2.2. Pero hay algo más que podemos aprender de esta milenaria representación: el número 10 no se representaba por medio de diez barras concatenadas, sino por dos signos diferentes: el primero, parecido a una semicircunferencia; el segundo, una barra horizontal.
Lo que resulta relevante es que el procedimiento de concatenación de unidades-barras se extiende a la concatenación de los nuevos signos de forma de representar nuevos números naturales. Así, por ejemplo, como se puede apreciar en la figura 2.4, el número 20 se representa de dos formas diferentes: la primera, poniendo dos signos tipo semicircunferencia que representan el 10, de manera que se obtiene una especie de circunferencia, o simplemente poniendo una barra horizontal arriba de otra. Similarmente con el número 30: tres barras horizontales, o tres semicircunferencias (dos de las cuales forman una circunferencia). El número 40 se representaba por medio de cuatro barras horizontales.
No solo aprendemos esto de dichas representaciones fenicias. Además aprendemos que el número 11 es la concatenación del signo utilizado para representar el 10 con el signo usado para representar el 1. Igualmente, el 21 corresponde a concatenar el signo del 1 con el signo del 20 (que es la concatenación de dos signos del 10). No deja de ser interesante el orden de la concatenación: el 11 se obtuvo concatenando un 10 y luego un 1, mientras que el 21 se obtuvo concatenando un 1 y un 20.
Figura 2.4: Numerales fenicios
Este “salto” debe ser enfatizado con tus estudiantes. Pregúntense cuál es su significación. Para ello, pide que cuenten la siguiente secuencia:
2 2 2 2 2 2 2 2 2
La respuesta es simple: hay nueve 2. Pero la actividad realizada es digna de ser entendida lo más cabalmente que se pueda: el 2 acaba de ser usado como signo susceptible de ser concatenado. Por lo tanto, un signo que abrevia una concatenación –el 2 como abreviación de
– puede a su vez ser utilizado como signo susceptible de ser concatenado.
2.1.3. El sistema numérico babilónico
El “salto” al que hacíamos referencia lo podemos apreciar con total transparencia al examinar...
Índice
Portada
Portadilla
Créditos
Dedicado a...
Índice
I Antes del Método Están Los Contenidos: Aspectos Fundantes
II Aprendamos Aritmética
III El Triángulo Aritmético de Pascal
IV Reflexiones Finales
V Apéndice: Construcción Rigurosa de La Aritmética
