Cómo funcionan nuestras gafas

Sergio Barbero Briones

• Editorial: Los Libros de La Catarata
• Año: 2016
• ISBN del libro electrónico: 9788483199695
• Categoría: Medicina
• Categoría: Oftalmología y optometría

Puede que el lector de este libro necesite usar unas gafas para leerlo o, quizás, puede que para llegar hasta la librería haya tenido que utilizarlas para ver de lejos. Si no es así, se trata, sin duda, de una persona afortunada, ya que en los países desarrollados más de la mitad de la población necesita unas gafas o algún otro instrumento óptico para poder ver bien. A pesar de que las gafas aparenten ser un objeto sencillo y sin mucha ciencia, su diseño, en particular el de algunas lentes como las progresivas, es una de las áreas de investigación actuales más complejas desde el punto de vista matemático y médico que existen en las ciencias de la visión. En esta obra se explica qué es la miopía, la hipermetropía, la presbicia o el astigmatismo y se dan las claves de cómo la ciencia, a lo largo de los siglos, ha conseguido ir compensando estos defectos y mejorar la calidad de vida de muchas personas.

CAPÍTULO 1

El ojo como instrumento óptico

Rayos de luz

En agosto de 1992, durante la guerra de Bosnia-Herzegovina, unas bombas incendiarias destruyeron la Biblioteca de Sa­­rajevo, verdadero símbolo de la ciudad. Tras el incendio, el periodista Gervasio Sánchez entraba en la sala principal de la biblioteca en ruinas. En ese preciso momento, entre los escombros, un haz de luz penetraba a través de un orificio de uno de los muros que a duras penas se mantenía en pie. La fotografía es verdaderamente impactante (se puede ver en el enlace http://www.elcultural.es/galerias/galeria_de_imagenes/29/ARTE/Gervasio_Sanchez_Sarajevo-_1992-2008), por lo que con el transcurso del tiempo se ha convertido en un símbolo de la barbarie de la guerra. La imagen pone de manifiesto otro fenómeno con el que todos estamos familiarizados: cuando un haz de luz atraviesa un lugar oscuro se puede comprobar claramente que la luz se propaga en línea recta; pero ¿por qué ocurre así?

Estamos tan acostumbrados al fenómeno de la propagación rectilínea de la luz que quizás, a pesar de considerarnos por naturaleza curiosos, nunca nos hallamos hecho esta pregunta. Los lúcidos pensadores griegos de la Antigüedad sí se preguntaron por ello. Y no solo eso, sino que además lo postularon como una ley básica de la naturaleza. Anaxágoras de Clazómenes afirmaba en el siglo V a.C.: “El que la tierra es plana se demuestra claramente por las salidas y puestas del sol y de la luna, en las cuales, tan pronto como aparece el brillo de la primera luz, esta se manifiesta a nuestra mirada en líneas rectas”. Obviamente, se equivocaba en lo que refiere a la forma de la Tierra.

A partir de una meticulosa observación de la naturaleza, Anaxágoras infirió que la luz necesariamente siempre debía propagarse siguiendo trayectorias rectas. Y dio un paso más importante aún: utilizando la lógica de la deducción se sirvió de este principio para mostrar las causas de fenómenos tan singulares como los eclipses o la apariencia de la Vía Láctea.

Los griegos fueron incluso capaces de dar una explicación al postulado de la propagación rectilínea de la luz. La explicación radicaba en un principio todavía más profundo: aquel que dice que la luz sigue siempre el camino más corto, el del mínimo esfuerzo. Y el camino más corto entre dos puntos dados es la línea que une ambos puntos, lo cual reco­­nocieron como un postulado —esto es una afirmación aceptada, pero no deducible— matemáticos de la talla de Euclides o Ar­­químedes.

Sin embargo, esto solo se cumple cuando la luz se mueve por un medio homogéneo. Un medio homogéneo, desde el punto de vista óptico, es aquel que tiene exactamente las mismas propiedades ópticas en cualquier punto del medio. Dicho de otra manera, la luz no modifica su trayectoria al atravesar el medio. En puridad solo existe un medio completamente homogéneo: el vacío. Los medios físicos reales se caracterizan por lo que se denomina índice de refracción. Podemos entender el índice de refracción, por analogía con la mecánica, como si fuese una medida de la densidad del medio en cuanto a su influencia en la velocidad de propagación de la luz. De hecho, el índice de refracción de un medio es el cociente entre la velocidad de la luz en ese medio y la velocidad de la luz en el vacío. Medios con índices de refracción altos conllevan, pues, menor velocidad de la luz que los medios con índices bajos. Esta interpretación mecánica fue la que desarrollo René Descartes (1596-1650). Como apéndice a su celebérrimo Discurso del método publicó un pequeño tratado, Dioptrique, en el que describe la luz como la propagación de un impulso mecánico.

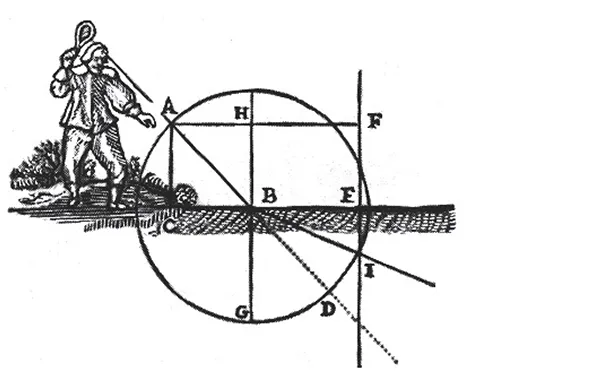
Descartes utilizó un esquema mecánico para explicar qué es lo que ocurre cuando un rayo de luz atraviesa dos medios de diferente índice de refracción. Imaginemos que lanzamos una bola, con ayuda de una raqueta, siguiendo una trayectoria rectilínea en el aire desde el punto A hasta el punto B (figura 1). Cuando la bola llega a este punto se encuentra con un medio diferente (una red) más denso que el aire. A partir de este punto la bola continuará una trayectoria rectilínea (desde el punto B hasta el punto I), pero irá a una velocidad más lenta y, además, cambiará su trayectoria.

Figura 1

Esquema de Descartes. Bola sigue trayectoria de A a B y de B a I.

Este cambio de trayectoria del rayo de luz, al encontrarse un medio diferente, es lo que nos interesa a nosotros. Se denomina refracción y depende de dos cosas: de la diferencia entre el índice de refracción (densidad) entre los dos medios y del ángulo de incidencia del rayo con respecto de la perpendicular a la superficie separadora. Esta ley, expresada matemáticamente, es una de las más importantes de la óptica: nsinθ = n’sinθ’ (n y n’ son los índices de refracción a un lado y otro de la superficie refractora; θ y θ’ son los ángulos de incidencia con la perpendicular a la superficie refractora). Esta ley se llama ley de la refracción y no se descubrió, que sepamos, hasta el siglo X por Ibn Sahl, un matemático relacionado con la corte de Bagdad. También se denomina a veces ley de Snell, por el matemático holandés Willebrord Snell, a quien durante cierto tiempo se acreditó como primer descubridor de la ley.

Lo descrito hasta ahora forma parte de la denominada teoría geométrica de la luz. La luz se propaga por medio de rayos que, al encontrar un medio diferente, se refractan, o alternativamente se reflejan, en el caso de que la superficie que separa los medios sea una superficie reflectora, como lo es un espejo. Aunque el fenómeno de propagación de la luz es en realidad más complejo, la teoría geométrica es esencialmente válida para explicar cómo las gafas afectan a nuestra visión.

El círculo que besa

El primer paso en el complejo fenómeno de la visión es el de la formación de imágenes. Nuestro ojo recoge la luz proveniente de objetos exteriores y la concentra en una delgada capa compuesta de células foto-receptoras denominada retina. Ya sabemos cómo se propaga un haz de rayos de luz. Ahora bien, ¿cómo produce el ojo una imagen de un objeto externo? El método científico se caracteriza por reducir un problema complejo a una serie de problemas acotados y más sencillos de resolver. Así que imaginemos que por el momento solo nos interesa averiguar cómo se forma la imagen de una estrella que estamos mirando en la oscuridad.

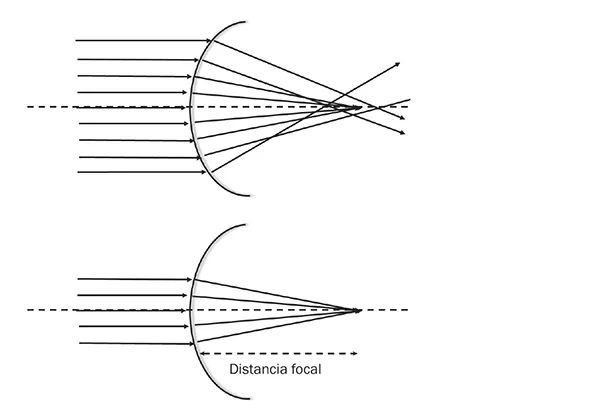
Observamos la estrella en una dirección determinada por la línea de mirada. Está situada muy lejos, por lo que los rayos de luz que de ella emanan, al llegar a nuestro ojo, inciden con una inclinación muy pequeña respecto de la línea de mirada. Por tanto, estos rayos se pueden considerar “paralelos”. Imaginemos que nuestro ojo, entendido como sistema formador de imágenes, está compuesto por una única capa separadora de medios —de hecho, como veremos, durante mucho tiempo se creyó que el ojo solo tenía una superficie con poder refractivo: la córnea— y una superficie donde se forma la imagen. Todos estos rayos, al refractarse (cambiar su dirección) en esta capa, siguen unas trayectorias que no necesariamente se cortan en un único punto en la superficie receptora, tal como se ve en la figura 2. Esto se traduce en que la imagen de la estrella se vería emborronada o desenfocada. Sin embargo, si empezamos a reducir la cantidad de rayos que entran en el sistema, por ejemplo, disminuyendo el tamaño de la apertura que deja entrar los rayos, llegará un momento en que to­­dos los rayos converjan prácticamente en un único punto. De­­cimos entonces que se produce una imagen de un punto objeto (estrella) en un punto imagen. En realidad, no vemos las estrellas como puntos, sino de forma estrellada (valga la redundancia). Esto se debe a otros fenómenos ópticos, tales como la difracción o la difusión.

Figura 2

Rayos centrales convergen mejor en un único punto.

Para entender por qué los rayos, según reducimos el tamaño de la apertura o pupila, empiezan a converger mejor, tenemos que recurrir a un concepto básico de la geometría: la curvatura. Empecemos con la curva más conocida: la circunferencia. El radio de una circunferencia nos dice lo grande o pequeña que es esta. La curvatura no es otra cosa que la inversa del radio de curvatura. De manera que si la curvatura es pequeña, el tamaño de la circunferencia será grande, y viceversa. En el extremo, si la curvatura es cero, la circunferencia se “convierte” en una línea recta. Por tanto, se dice que un círculo es más o menos curvo dependiendo del valor de la curvatura de la circunferencia asociada.

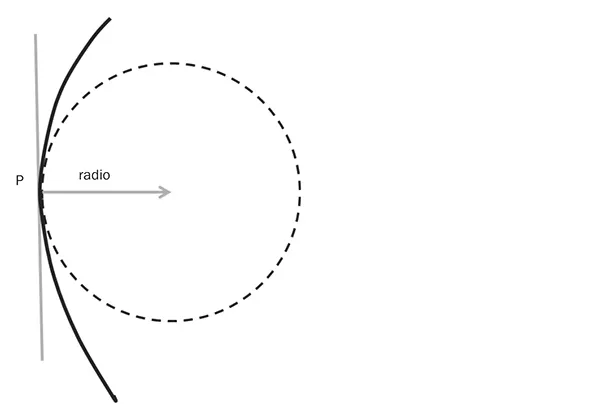
Cojamos ahora una curva cualquiera, como la marcada por la línea gruesa en la figura 3, y un punto P perteneciente a ella. Existe un círculo que “toca” a la curva en el punto P, en el sentido que solo coincide con la curva en el punto P, y que tiene unas propiedades especiales. Gottfried W. Leibniz (1646-1716), genio a la altura de Isaac Newton, bautizó a este círculo como circulus osculans (del latín osculate, que significa “beso”), esto es, el círculo que besa a la curva en P. Lo que hay que recordar es que la curvatura de la curva en el punto P es igual a la del circulus osculans en ese punto. Cuando la curvatura es muy grande decimos que la curva está muy curvada en ese punto. Por otro lado, si la curvatura es muy pequeña, entonces se dice que la curva es poco curvada o muy plana.

Volvamos al problema óptico de la figura 2. Podemos ver que si la superficie tuviese una curvatura muy grande, los rayos incidentes formarían un ángulo mayor con la superficie refractora (en particular con la recta perpendicular a la superficie). Ya que la ley de la refracción nos dice que la refracción de los rayos aumenta cuanto mayor es el ángulo de incidencia, podemos concluir que también la refracción aumenta con mayores curvaturas del circulus osculans.

El poder refractivo de una superficie viene dado por la distancia desde el vértice de la superficie hasta el punto donde convergen los rayos. A esta distancia se la llama distancia focal. De manera análoga a la curvatura y al radio de curvatura, se puede definir la potencia óptica como la inversa de la distancia focal.

Figura 3

El círculo que besa.

Aunque a primera vista pueda parecer que la potencia óptica es igual a la curvatura, esto no es así, ya que la diferencia de índices de refracción también es importante. Motivado por entender mejor cómo forma imágenes un telescopio, Christian Huygens, en un tratado escrito en 1653, demostró, usando argumentos geométricos, que la potencia óptica es igual a la curvatura multiplicada por la diferencia de los índic...

Índice

• Presentación
• Prólogo
• Capítulo 1. El ojo como instrumento óptico
• Capítulo 2. Defectos ópticos de la visión
• Capítulo 3. Antes del anteojo
• Capítulo 4. ¿Cómo funciona una lente?
• Capítulo 5. ¡Quiero ver bien de lejos y de cerca!
• Epílogo. Mirando el futuro a través de lentes
• Cronología
• Bibliografía