Modelos discretos en epidemiología

Influenza AH1N1 y COVID-19 pandemias del siglo XXI

Paula Andrea González Parra, Carlos Castillo-Chávez

• Editorial: Autónoma de Occidente
• Año: 2022
• ISBN del libro electrónico:
  9789586190947
• Categoría: Medicina
• Categoría: Epidemiologia

Con la aparición del COVID-19, ha crecido en la población general el interés en los modelos matemáticos de las enfermedades infecciosas. Es común escuchar sobre el número reproductivo básico R, el pico de la pandemia, las políticas de mitigación de la enfermedad, entre otras. Una de las contribuciones más importantes en epidemiología matemática es el modelo comportamental propuesto por Kermack y McKendrick formulado en 1927.

Capítulo 1

Modelo SIR

Una de las contribuciones más importantes en epidemiología matemática es el modelo compartamental propuesto por Kermack y McKendrick formulado en 1927 [1, 2, 3, 4], el cual es un modelo continuo basado en el flujo de individuos entre diferentes clases.

En particular es bien conocido el clásico modelo SIR, en el que la población total es dividida en Susceptibles (personas que no han contraido la enfermedad y podrían ser infectados), Infectados (personas que han adquirido la enfermedad y pueden transmitirla a otros individuos) y Removidos o Recuperados (individuos que estuvieron infectados y ya se recuperaron de la enfermedad). En la Figura 1.1 se muestra el diagrama de flujo de la dinámica de la enfermedad para el modelo continuo SIR. En este diagrama cada compartimento representa una clase de individuos; Susceptibles (S) - Infectados (I) - Recuperados (R), las personas se mueven de un compartimento a otro cuando cambia su estado en la epidemia.

Diagrama modelo continuo SIR

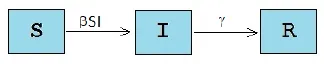
Figura 1.1: Diagrama de flujo compartamental para el modelo SIR. Los individuos se mueven de un compartimento a otro cuando cambia su estado epidemiológico. Un susceptible (S) pasa a ser infectado (I) o un infectado (I) pasa a ser recuperado (R).

El modelo está dado por el sistema de ecuaciones diferenciales:

En este modelo no se tienen en cuenta efectos demográficos; es decir, no hay nacimientos ni muertes, tampoco se considera mortalidad debido a la enfermedad. La transmisión de la enfermedad se da teniendo en cuenta la ley de acción de masas, así pues, el término βSI representa el número de individuos que pasa de la clase S a la clase I.

1.1.Presentación del modelo discreto SIR

En los últimos años se ha incrementado el interés en el uso de modelos discretos para estudiar la dinámica de las enfermedades transmisibles [1, 5, 6, 7, 8], sin embargo no son muchos los estudios en los que se consideran modelos discretos. Aunque matemáticamente son un poco más complejos, los resultados son más fáciles de comparar con los datos experimentales dado que los datos son obtenidos en intervalos discretos de tiempo (días, semanas, meses, entre otros).

Se presenta a continuación la versión discreta del modelo SIR. Para esto se siguen las ideas presentadas en [20, 21], de manera similar a la versión continua presentada, no se tienen en cuenta nacimientos y muertes por causas naturales, ya que se considera un único brote de la enfermedad. En el modelo, el subindice t es utilizado para denotar el número de individuos de cada clase en el tiempo t; es decir, S_t, I_t, y R_t, representan el número de susceptibles, infectados y recuperados en el tiempo t, para t en el intervalo [0, n], donde n denota el tiempo final de un brote único de la enfermedad.

...

Índice

• Cubierta
• Portada
• Créditos
• Índice general
• Introducción
• 1 Modelo SIR
• 2 Control óptimo en epidemiología
• 3 Control óptimo aplicado a un modelo de influenza
• 4 Cuando los recursos son limitados
• 5 Cuando algunos grupos son más vulnerables
• 6 Modelo de propagación del COVID-19
• Conclusiones
• Bibliografía