![]()
Why Do Fractals Matter?
John Archibald Wheeler (b. 1911), protégé of the quantum pioneer Niels Bohr and friend of Albert Einstein, has been at the cutting edge of 20th-century physics, cosmology and quantum theory. Ian Stewart is a respected Professor of Mathematics at Warwick University. They are among the many scientists agreed that fractal geometry is a revolutionary breakthrough in our comprehension of reality.
A Smooth World or a Rough One?
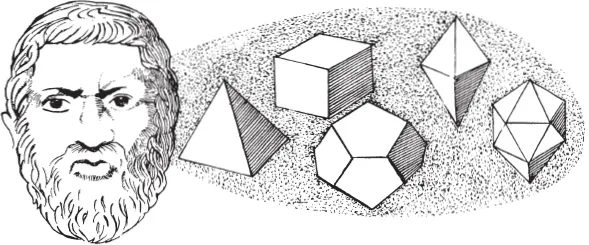
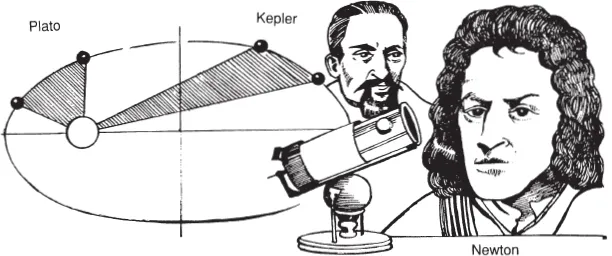
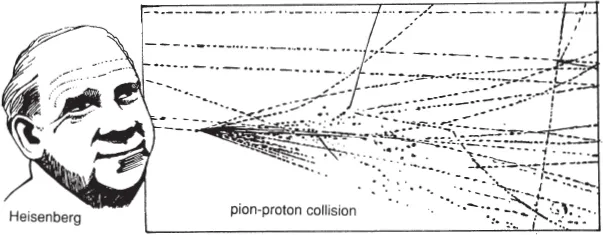
Plato sought to explain nature with five regular solid forms. Newton and Kepler bent Plato’s circle into an ellipse. Modern science analysed Plato’s shapes into particles and waves, and generalised the curves of Newton and Kepler to relative probabilities – still without a single “rough edge”. Now, more than two thousand years after Plato, nearly three hundred years after Newton, Benoît Mandelbrot has established a discovery that ranks with the laws of regular motion. Professor Eugene Stanley, Center for Polymer Studies, Department of Physics, Boston University
The world that we live in is not naturally smooth-edged. The real world has been fashioned with rough edges. Smooth surfaces are the exception in nature. And yet, we have accepted a geometry that only describes shapes rarely – if ever – found in the real world. The geometry of Euclid describes ideal shapes – the sphere, the circle, the cube, the square. Now these shapes do occur in our lives, but they are mostly man-made and not nature-made.
The Texture of Reality
Nature deals in non-uniform shapes and rough edges. Take the human form. There is a certain symmetry about it, but it is, and has always been, indescribable in terms of Euclidean geometry. It is not a uniform shape. This is the issue. What has been missing from the scientific repertoire until very recently has been a way of describing the shapes and objects of the real world.
The word “fractal” was coined in 1975 by the Polish/French/American mathematician, Benoît Mandelbrot (b. 1924), to describe shapes which are detailed at all scales. He took the word from the Latin root fractus, suggesting fragmented, broken and discontinuous.
Fractal geometry is the geometry of the irregular shapes we find in nature, and in general fractals are characterized by infinite detail, infinite length, and the absence of smoothness or derivative.
The Origins of Fractals
Fractal geometry is an extension of classical geometry. It does not replace classical geometry, but enriches and deepens its powers. Using computers, fractal geometry can make precise models of physical structures – from sea-shells to galaxies.
We will now trace the historical development of this mathematical discipline and explore its descriptive powers in the natural world, then look at the applications in science and technology and at the implications of the discovery.
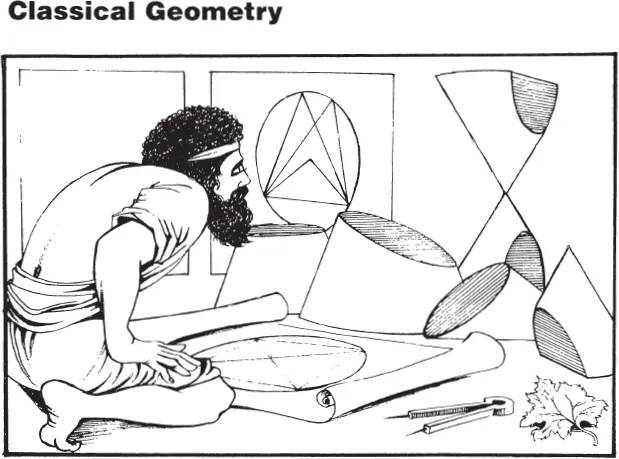
Euclid of Alexandria (c. 300 BC) laid down the rules which were to define the subject of geometry for millennia to come. The shapes that Euclid studied – straight lines and circles – proved so successful in explaining the universe that scientists became blind to their limitations, denouncing patterns that did not fit in Euclid’s scheme as “counterintuitive” and even “pathological”.
A steady undercurrent of ideas, starting in the 19th century with discoveries by Karl Weierstrass (1815–97), Georg Cantor (1845–1918) and Henri Poincaré (1845–1912), led inexorably towards the creation of a whole new kind of geometry, with the power to describe aspects of the world inexpressible in the basic language of Euclid.
The Calculus
Johannes Kepler (1571–1630) was the first to realize that planets followed elliptical orbits, not perfect circles. Edmond Halley (1656–1742) guessed that elliptical orbits could be explained, by analogy with light, using an inverse square law.
Sir Isaac Newton (1642–1727) derived a new method of reasoning based on the idea of vanishingly small quantities, or infinitesimals, in order to tame the complex motions of projectiles and planets and arrive at his celebrated theory of universal gravitation. The calculus was conceived simultaneously by Newton and Gottfried Wilhelm Leibniz (1646–1716). Leibniz developed the clearest formulation of the...