The Crest of the Peacock

Non-European Roots of Mathematics - Third Edition

George Gheverghese Joseph

• Editorial: Princeton University Press
• Año: 2010
• ISBN:
  9781400836369
• Edición: 3
• Categoría: Sciences physiques
• Categoría: Physique

From the Ishango Bone of central Africa and the Inca quipu of South America to the dawn of modern mathematics, The Crest of the Peacock makes it clear that human beings everywhere have been capable of advanced and innovative mathematical thinking. George Gheverghese Joseph takes us on a breathtaking multicultural tour of the roots and shoots of non-European mathematics. He shows us the deep influence that the Egyptians and Babylonians had on the Greeks, the Arabs' major creative contributions, and the astounding range of successes of the great civilizations of India and China.
The third edition emphasizes the dialogue between civilizations, and further explores how mathematical ideas were transmitted from East to West. The book's scope is now even wider, incorporating recent findings on the history of mathematics in China, India, and early Islamic civilizations as well as Egypt and Mesopotamia. With more detailed coverage of proto-mathematics and the origins of trigonometry and infinity in the East, The Crest of the Peacock further illuminates the global history of mathematics.

Chapter One

The History of Mathematics: Alternative Perspectives

A Justification for This Book

An interest in history marks us for life. How we see ourselves and others is shaped by the history we absorb, not only in the classroom but also from the Internet, films, newspapers, television programs, novels, and even strip cartoons. From the time we first become aware of the past, it can fire our imagination and excite our curiosity: we ask questions and then seek answers from history. As our knowledge develops, differences in historical perspectives emerge. And, to the extent that different views of the past affect our perception of ourselves and of the outside world, history becomes an important point of reference in understanding the clash of cultures and of ideas. Not surprisingly, rulers throughout history have recognized that to control the past is to master the present and thereby consolidate their power.

During the last four hundred years, Europe and its cultural dependencies¹ have played a dominant role in world affairs. This is all too often reflected in the character of some of the historical writing produced by Europeans in the past. Where other people appear, they do so in a transitory fashion whenever Europe has chanced in their direction. Thus the history of the Africans or the indigenous peoples of the Americas often appears to begin only after their encounter with Europe.

An important aspect of this Eurocentric approach to history is the manner in which the history and potentialities of non-European societies were represented, particularly with respect to their creation and development of science and technology. The progress of Europe during the last four hundred years is often inextricably—or even causally—linked with the rapid growth of science and technology during the period. In the minds of some, scientific progress becomes a uniquely European phenomenon, which can be emulated by other nations only if they follow a specifically European path of scientific and social development.

Such a representation of societies outside the European cultural milieu raises a number of issues that are worth exploring, however briefly. First, these societies, many of them still in the grip of an intellectual dependence that is the legacy of European political domination, should ask themselves some questions. Was their indigenous scientific and technological base innovative and self-sufficient during their precolonial period? Case studies of India, China, and parts of Africa, contained, for example, in the work of Dharampal (1971), Needham (1954), and Van Sertima (1983) and summarized by Teresi (2002), seem to indicate the existence of scientific creativity and technological achievements long before the incursions of Europe into these areas. If this is so, we need to understand the dynamics of precolonial science and technology in these and other societies and to identify the material conditions that gave rise to these developments. This is essential if we are to see why modern science did not develop in these societies, only in Europe, and to find meaningful ways of adapting to present-day requirements the indigenous and technological forms that still remain.²

Second, there is the wider issue of who “makes” science and technology. In a material and nonelitist sense, each society, impelled by the pressures and demands of its environment, has found it necessary to create a scientific base to cater to its material requirements. Perceptions of what constitute the particular requirements of a society would vary according to time and place, but it would be wrong to argue that the capacity to “make” science and technology is a prerogative of one culture alone.

Third, if one attributes all significant historical developments in science and technology to Europe, then the rest of the world can impinge only marginally, either as an unchanging residual experience to be contrasted with the dynamism and creativity of Europe, or as a rationale for the creation of academic disciplines congealed in subjects such as development studies, anthropology, and oriental studies. These subjects in turn served as the basis from which more elaborate Eurocentric theories of social development and history were developed and tested.³

One of the more heartening aspects of academic research in the last four or five decades is that the shaky foundations of these “adjunct” disciplines are being increasingly exposed by scholars, a number of whom originate from countries that provide the subject matter of these disciplines. “Subversive” analyses aimed at nothing less than the unpackaging of prevailing Eurocentric paradigms became the major preoccupation of many of these scholars. Syed Husain Alatas (1976) studied intellectual dependence and imitative thinking among social scientists in developing countries. The growing movement toward promoting a form of indigenous anthropology that sees its primary task as questioning, redefining, and if necessary rejecting particular concepts that grew out of colonial experience in Western anthropology is thoroughly examined by Fahim (1982). Edward Said (1978) has brilliantly described the motives and methods of the so-called orientalists who set out to construct a fictitious entity called “the Orient” and then ascribe to it qualities that are a mixture of the exotic, the mysterious, and the otherworldly. The rationale for such constructs is being examined in terms of the recent history of Europe's relations with the rest of the world.

In a similar vein, and in the earlier editions of this book, it was the intention to show that the standard treatment of the history of non-European mathematics exhibited a deep-rooted historiographical bias in the selection and interpretation of facts, and that mathematical activity outside Europe has as a consequence been ignored, devalued, or distorted. It is interesting in this context that since the first edition of this book there has been a growing recognition of the mathematics outside the European and Greek traditions, especially in the mainstream teaching of the history of mathematics. The Eurocentric argument has shifted its ground and now questions both the nature of the European debt to other mathematical traditions and the existence and quality of proofs and demonstrations in traditions outside Europe. A brief discussion of the shifting ground of Eurocentrism in the history of mathematics is found in the preface to this edition.⁴

The Development of Mathematical Knowledge

A concise and meaningful definition of mathematics is difficult. In the context of this book, the following aspects of the subject are highlighted. Modern mathematics has developed into a worldwide language with a particular kind of logical structure. It contains a body of knowledge relating to number and space, and prescribes a set of methods for reaching conclusions about the physical world. And it is an intellectual activity which calls for both intuition and imagination in deriving “proofs” and reaching conclusions. Often it rewards the creator with a strong sense of aesthetic satisfaction.

The “Classical” Eurocentric Trajectory

Most histories of mathematics that have had a great influence on later work were written in the late nineteenth or early twentieth century. During that period, two contrasting developments were taking place that had an impact on both the content and the balance of these books, especially those produced in Britain and the United States. Exciting discoveries of ancient mathematics on papyri in Egypt and clay tablets in Mesopotamia pushed back the origins of written mathematical records by at least fifteen hundred years. But a far stronger and countervailing influence was the culmination of European domination in the shape of political control of vast tracts of Africa and Asia. Out of this domination arose the ideology of European superiority that permeated a wide range of social and economic activities, with traces to be found in histories of science that emphasized the unique role of Europe in providing the soil and spirit for scientific discovery. The contributions of the colonized peoples were ignored or devalued as part of the rationale for subjugation and dominance. And the development of mathematics before the Greeks—notably in Egypt and Mesopotamia—suffered a similar fate, dismissed as of little importance to the later history of the subject. In his book Black Athena (1987), Martin Bernal has shown how respect for ancient Egyptian science and civilization, shared by ancient Greece and pre-nineteenth-century Europe alike, was gradually eroded, leading eventually to a Eurocentric model with Greece as the source and Europe as the inheritor and guardian of the Greek heritage.

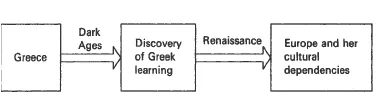
Figure 1.1 presents the “classical” Eurocentric view of how mathematics developed over the ages. This development is seen as taking place in two sections, separated by a period of stagnation lasting for over a thousand years: Greece (from about 600 BC to AD 400), and post-Renaissance Europe from the sixteenth century to the present day. The intervening period of inactivity was the “Dark Ages”—a convenient label that expressed both post-Renaissance Europe's prejudices about its immediate past and the intellectual self-confidence of those who saw themselves as the true inheritors of the “Greek miracle” of two thousand years earlier.

Two passages, one by a well-known historian of mathematics writing at the turn of the century and the other by a more recent writer whose books are still referred to on both sides of the Atlantic, show the durability of this Eurocentric view and its imperviousness to new evidence and sources:

FIGURE 1.1: The “classical” Eurocentric trajectory

The history of mathematics cannot with certainty be traced back to any school or period before that of the Ionian Greeks. (Rouse Ball 1908, p. 1)

[Mathematics] finally secured a new grip on life in the highly congenial soil of Greece and waxed strongly for a short period…. With the decline of Greek civilization the plant remained dormant for a thousand years…when the plant was transported to Europe proper and once more imbedded in fertile soil. (Kline 1953, pp. 9-10)

The first statement is a reasonable summary of what was popularly known and accepted as the origins of mathematics at that time, except for the neglect of the early Indian mathematics contained in the Sulbasutras (The Rules of the Cord), belonging to the period between 800 and 500 BC, which would make it at least as old as the earliest-known Greek mathematics. Thibaut's translations of these works, made around 1875, were known to historians of mathematics at the turn of the century. The mathematics contained in the Sulbasutras is discussed in chapter 8.

The second statement, however, ignores a considerable body of research evidence pointing to the development of mathematics in Mesopotamia, Egypt, China, pre-Columbian America, India, and the Islamic world that had come to light in the intervening period. Subsequent chapters will bear testimony to the volume and quality of the mathematics developed in these areas. But in both these quotations mathematics is perceived as an exclusive product of European civilization. And that is the central message of the Eurocentric trajectory depicted in figure 1.1.

This comforting rationale for European dominance became increasingly untenable for a number of reasons. First, there is the full acknowledgment given by the ancient Greeks themselves of the intellectual debt they owed the Egyptians. There are scattered references from Herodotus (c. 450 BC) to Proclus (c. AD 400) of the knowledge acquired from the Egyptians in fields such as astronomy, mathematics, and surveying, while other commentators even considered the priests of Memphis to be the true founders of science.

To Aristotle (c. 350 BC), Egypt was the cradle of mathematics. His teacher, Eudoxus, one of the notable mathematicians of the time, had studied in Egypt before teaching in Greece. Even earlier, Thales (d. 546 BC), the legendary founder of Greek mathematics, and Pythagoras (c. 500 BC), one of the earliest and greatest of Greek mathematicians, were reported to have traveled widely in Egypt and Mesopotamia and learned much of their mathematics from these areas. Some sources even credit Pythagoras with having traveled as far as India in search of knowledge, which could explain some of the parallels between Indian and Pythagorean philosophy and religion.⁵

A second reason why the trajectory depicted in figure 1.1 was found to be wanting arose from the combined efforts of archaeologists, translators, and interpreters, who between them unearthed evidence of a high level of mathematics practiced in Mesopotamia and in Egypt at the beginning of the second millennium, providing further confirmation of Greek reports. In particular, the Mesopotamians had invented a place-value number system, knew different methods of solving what today would be described as quadratic equations (methods that would not be improved upon until the sixteenth century AD), and understood (but had not proved) the relationship between the sides of a right-angled triangle that came to be known as the Pythagorean theorem.⁶ Indeed, as we shall see in later chapters, this theorem was stated and demonstrated in different forms all over the world.

A four-thousand-year-old clay tablet, kept in a Berlin museum, gives the value of n³ + n² for n = 1, 2,…, 10, 20, 30, 40, 50, from which it has been surmised that the Mesopotamians may have used these values in solving cubic equations after reducing them to the form x³ + x² = c. A remarkable solution in Egyptian geometry found in the Moscow Papyrus from the Middle Kingdom (c. 2000-1800 BC) follows from the correct use of the formula for the volume of a truncated square pyramid. These examples and other milestones will be discussed in the relevant chapters of this book.

The neglect of the Islamic contribution to the development of European intellectual life in general and mathematics in particular is another serious drawback of the “classical” view. The course of European cultural history and the history of European thought are inseparably tied up with the activities of Islamic scholars during the Middle Ages and their seminal contributions to mathematics, the natural sciences, medicine, and philosophy.⁷ In particular, we owe to the Islamic world in the field of mathematics the bringing together of the technique of measurement, evolved from its Egyptian roots to its final form in the hands of the Alexandrians, and the remarkable instrument of computation (our number system) that originated in India. These strands were supplemented by a systematic and consistent language of calculation that came to be known by its Arabic name, algebra. An acknowledgment of this debt in more recent books contrasts sharply with the neglect of other Islamic contributions to science.⁸

Finally, in discussing the Greek contribution, there is a need to recognize the differences between the Classical period of Greek civilization (i.e., from about 600 to 300 BC) and the post-Alexandrian period (i.e., from about 300 BC to AD 400). In early European scholarship, the Greeks of the ancient world were perceived as an ethnically homogeneous group, originating from areas that were mainly within the geographical boundaries of present-day Greece. It was part of the Eurocentric mythology that from the mainland of Europe had emerged a group of people who had created, virtually out of nothing, the most impressive civilization of ancient times. And from that civilization had emerged not only the cherished institutions of present-day Western culture but also the mainspring of modern science. The reality, however, is different and more complex. The term “Greek,” when applied to times before the appearance of Alexander (356-323 BC), really refers to a number of independent city-states, often at war with one another but exhibiting close ethnic or cultural affinities and, above all, sharing a common language. The conquests of Alexander changed the situation dramatically, for at his death his empire was divided among his generals, who established separate dynasties. The two notable dynasties from the point of view of mathematics were the Ptolemaic dynasty of Egypt and the Seleucid dynasty, which ruled over territories that included the earlier sites of the Mesopotamian civilization. The most famous center of learning and trade became Alexandria in Egypt, established in 332 BC and named after the conqueror. From its foundation, one of its most striking features was its cosmopolitanism—part Egyptian, part Greek, with a liberal sprinkling of Jews, Persians, Phoenicians, and Babylonians, and even attracting scholars and traders from as far away as India. A lively contact was maintained with the Seleucid dynasty. Alexandria thus became the meeting place for ideas and different traditions. The character of Greek mathematics began to change slowly, mainly as a result of continuing cross-fertilization between different mathematical traditions, notably the algebraic and empirical basis of Mesopotamian and Egyptian mathematics interacting with the geometric and antiempirical traditions of Greek mathematics. And from this mixture came some of the greatest mathematicians of antiquity, notably Archimedes and Diophantus. It is therefore important to recognize the Alexandrian dimension to Greek mathematics while noting that Greek intellectual and cultural traditions served as the main inspiration and the Greek language as the medium of instruction and writing in Alexandria. In a later chapter, based on some innovative work of Friberg (2005, 2007), we will examine the close and hitherto unexamined links between Egyptian, Mesopotamian, and Greek mathematics.

A Modi...