![]()
CHAPTER 1
Introduction to Cryptography and Cryptocurrencies
All currencies need some way to control supply and enforce various security properties to prevent cheating. In fiat currencies, organizations like central banks control the money supply and add anticounterfeiting features to physical currency. These security features raise the bar for an attacker, but they don’t make money impossible to counterfeit. Ultimately, law enforcement is necessary for stopping people from breaking the rules of the system.
Cryptocurrencies too must have security measures that prevent people from tampering with the state of the system and from equivocating (that is, making mutually inconsistent statements to different people). If Alice convinces Bob that she paid him a digital coin, for example, she should not be able to convince Carol that she paid her that same coin. But unlike fiat currencies, the security rules of cryptocurrencies need to be enforced purely technologically and without relying on a central authority.
As the word suggests, cryptocurrencies make heavy use of cryptography. Cryptography provides a mechanism for securely encoding the rules of a cryptocurrency system in the system itself. We can use it to prevent tampering and equivocation, as well as to encode, in a mathematical protocol, the rules for creation of new units of the currency. Thus, before we can properly understand cryptocurrencies, we need to delve into the cryptographic foundations that they rely on.
Cryptography is a deep academic research field using many advanced mathematical techniques that are notoriously subtle and complicated. Fortunately, Bitcoin relies on only a handful of relatively simple and well-known cryptographic constructions. In this chapter, we specifically study cryptographic hashes and digital signatures, two primitives that prove to be useful for building cryptocurrencies. Later chapters introduce more complicated cryptographic schemes, such as zero-knowledge proofs, that are used in proposed extensions and modifications to Bitcoin.
Once the necessary cryptographic primitives have been introduced, we’ll discuss some of the ways in which they are used to build cryptocurrencies. We’ll complete this chapter with examples of simple cryptocurrencies that illustrate some of the design challenges that need to be dealt with.
1.1. CRYPTOGRAPHIC HASH FUNCTIONS
The first cryptographic primitive that we need to understand is a cryptographic hash function. A hash function is a mathematical function with the following three properties:
• Its input can be any string of any size.
• It produces a fixed-sized output. For the purpose of making the discussion in this chapter concrete, we will assume a 256-bit output size. However, our discussion holds true for any output size, as long as it is sufficiently large.
• It is efficiently computable. Intuitively this means that for a given input string, you can figure out what the output of the hash function is in a reasonable amount of time. More technically, computing the hash of an n-bit string should have a running time that is O(n).
These properties define a general hash function, one that could be used to build a data structure, such as a hash table. We’re going to focus exclusively on cryptographic hash functions. For a hash function to be cryptographically secure, we require that it has the following three additional properties: (1) collision resistance, (2) hiding, and (3) puzzle friendliness.
We’ll look more closely at each of these properties to gain an understanding of why it’s useful to have a function that satisfies them. The reader who has studied cryptography should be aware that the treatment of hash functions in this book is a bit different from that in a standard cryptography textbook. The puzzle-friendliness property, in particular, is not a general requirement for cryptographic hash functions, but one that will be useful for cryptocurrencies specifically.
Property 1: Collision Resistance
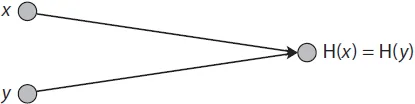
The first property that we need from a cryptographic hash function is that it is collision resistant. A collision occurs when two distinct inputs produce the same output. A hash function H(·) is collision resistant if nobody can find a collision (Figure 1.1). Formally:
Collision resistance. A hash function H is said to be collision resistant if it is infeasible to find two values, x and y, such that x ≠ y, yet H(x) = H(y).
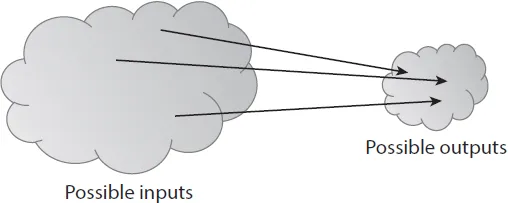
Notice that we said “nobody can find” a collision, but we did not say that no collisions exist. Actually, collisions exist for any hash function, and we can prove this by a simple counting argument. The input space to the hash function contains all strings of all lengths, yet the output space contains only strings of a specific fixed length. Because the input space is larger than the output space (indeed, the input space is infinite, while the output space is finite), there must be input strings that map to the same output string. In fact, there will be some outputs to which an infinite number of possible inputs will map (Figure 1.2).
FIGURE 1.1. A hash collision. x and y are distinct values, yet when input into hash function H, they produce the same output.
Now, to make things even worse, we said that it has to be impossible to find a collision. Yet there are methods that are guaranteed to find a collision. Consider the following simple method for finding a collision for a hash function with a 256-bit output size: pick 2256 + 1 distinct values, compute the hashes of each of them, and check whether any two outputs are equal. Since we picked more inputs than possible outputs, some pair of them must collide when you apply the hash function.
The method above is guaranteed to find a collision. But if we pick random inputs and compute the hash values, we’ll find a collision with high probability long before examining 2256 + 1 inputs. In fact, if we randomly choose just 2130 + 1 inputs, it turns out there’s a 99.8 percent chance that at least two of them are going to collide. That we can find a collision by examining only roughly the square root of the number of possible outputs results from a phenomenon in probability known as the birthday paradox. In the homework questions (see the online supplementary material for this book, which can be found at http://press.princeton.edu/titles/10908.html), we examine this in more detail.
FIGURE 1.2. Inevitability of collisions. Because the number of inputs exceeds the number of outputs, we are guaranteed that there must be at least one output to which the hash function maps more than one input.
This collision-detection algorithm works for every hash function. But, of course, the problem is that it takes a very long time to do. For a hash function with a 256-bit output, you would have to compute the hash function 2256 + 1 times in the worst case, and about 2128 times on average. That’s of course an astronomically large number—if a computer calculates 10,000 hashes per second, it would take more than one octillion (1027) years to calculate 2128 hashes! For another way of thinking about this, we can say that if every computer ever made by humanity had been computing since the beginning of the universe, the odds that they would have found a collision by now are still infinitesimally small. So small that it’s far less than the odds that the Earth will be destroyed by a giant meteor in the next two seconds.
We have thus found a general but impractical algorithm to find a collision for any hash function. A more difficult question is: Is there some other method that could be used on a particular hash function to find a collision? In other words, although the generic collision detection algorithm is not feasible to use, there may be some other algorithm that can efficiently find a collision for a specific hash function.
Consider, for example, the following hash function:
H(x)= x mod 2256
This function meets our requirements of a hash function as it accepts inputs of any length, returns a fixed-sized output (256 bits), and is efficiently computable. But this function also has an efficient method for finding a collision. Notice that this function just returns the last 256 bits of the input. One collision, then, would be the values 3 and 3 + 2256. This simple example illustrates that even though our generic collision detection method is not usable in practice, there are at least some hash functions for which an efficient collision detection method does exist.
Yet for other hash functions, we don’t know whether such methods exist. We suspect that they are collision resistant. However, no hash functions have been proven to be collision resistant. The cryptographic hash functions that we rely on in practice are just functions for which people have tried really, really hard to find collisions and haven’t yet succeeded. And so we choose to believe that those are collision resistant. (In some cases, such as the hash function known as MD5, collisions were eventually found after years of work, resulting in the function being deprecated and phased out of practical use.)
APPLICATION: MESSAGE DIGESTS
Now that we know what collision resistance is, the logical question is: What is it useful for? Here’s one application: If we know that two inputs x and y to a collision-resistant hash function H are different, then it’s safe to assume that their hashes H(x) and H(y) are different—if someone knew an x and y that were different but had the same hash, that would violate our assumption that H is collision resistant.
This argument allows us to use hash outputs as a message digest. Consider SecureBox, an authenticated online file storage system that allows users to upload files and to ensure their integrity when they download them. Suppose that Alice uploads really large files, and she wants to be able to verify later that the file she downloads is the same as the one she uploaded. One way to do that would be to save the whole big file locally, and directly compare it to the file she downloads. While this works, it largely defeats the purpose of uploading it in the first place; if Alice needs to have access to a local copy of the file to ensure its integrity, she can just use the local copy directly.
Collision-resistant hashes provide an elegant and efficient solution to this problem. Alice just needs to remember the hash of the original file. When she later downloads the file from SecureBox, she computes the hash of the downloaded file and compares it to the one she stored. If the hashes are the same, then she can conclude that the file is indeed the same one she uploaded, but if they are different, then Alice can conclude that the file has been tampered with. Remembering the hash thus allows her to detect not only accidental corruption of the file during transmission or on SecureBox’s servers but also intentional modification of the file by the server. Such guarantees in the face of potentially malicious behavior by other entities are at the core of what cryptography gives us.
The hash serves as a fixed-length digest, or unambiguous summary, of a message. This gives us a very efficient way to remember things we’ve seen before and to recognize them again. Whereas the entire file might have been gigabytes long, the hash is of fixed length—256 bits for the hash function in our example. This greatly reduces o...