A Quick Introduction to Complex Analysis

Kalyan Chakraborty, Shigeru Kanemitsu;Takako Kuzumaki

• Editorial: WSPC
• Año: 2016
• ISBN:
  9789813108530
• Categoría: Mathematics
• Categoría: Complex Analysis

The aim of the book is to give a smooth analytic continuation from calculus to complex analysis by way of plenty of practical examples and worked-out exercises. The scope ranges from applications in calculus to complex analysis in two different levels.

Chapter 1

A Quick Introduction to Complex Analysis with Applications

1.1The quickest introduction to complex analysis

This section serves as a review or survey material for those who are in a hurry to recall what the main ingredients in complex analysis are in three days. It presupposes some basic knowledge of complex numbers and functions etc. If you encounter something whose meaning is not clear to you, you must make a recourse to a more standard presentation of the theory in the subsequent sections.

Since complex function theory is in a sense infinitesimal calculus of complex-valued functions in the complex variable, it follows that the most fundamental ingredients in the theory are differentiation and integration; the former of which we define in the same way as with real functions, i.e. the function f(z) is differentiable at z = z₀ in its domain of definition D if

exists, in which case, the limit value is denoted by f′(z₀) called the derivative of f at z₀. Formally this is the same as the derivative of a real function, the only difference being that the limit is taken in a planar domain D ⊂ ℂ.

On the other hand, the latter is more complicated since integration means a contour integral. However, the below-mentioned “performing the change of variable principle” makes it quite easily accessible.

Definition 1.1. We say that a complex function is analytic (or sometimes holomorphic or regular) in a domain if it is differentiable at each point of the domain, where differentiability means the existence of the derivative, and a domain (sometimes referred to as a region) mathematically means a connected set; we simply understand a domain to be a certain plane figure (⊂ ℂ) with interior and with the boundary curve. We usually assume that domains are arc-wise connected. Typical domains are the rectangles (parallelopipeds) and circles and there is no need to worry about what domains are.

We assume throughout that a curve is a piecewise smooth (Jordan) curve described by the parametric expression

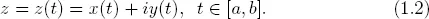
E.g., the unit circle C: ∣z∣ = 1 is given by

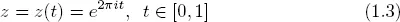
or by

C: z = z(t) = e^it, t ∈ [0, 2π],

where the complex exponential function e^it, cf. §1.3.2.

By the Jordan curve theorem, such a curve encircles a ...