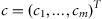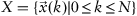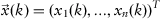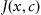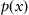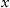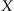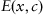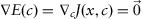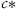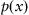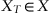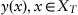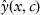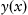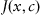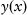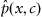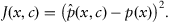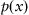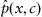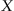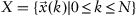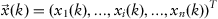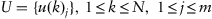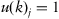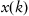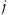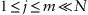Self-Learning and Adaptive Algorithms for Business Applications

A Guide to Adaptive Neuro-Fuzzy Systems for Fuzzy Clustering Under Uncertainty Conditions

Zhengbing Hu, Yevgeniy V. Bodyanskiy, Oleksii Tyshchenko

• Editorial: Emerald Publishing Limited
• Año: 2019
• ISBN:
  9781838671730
• Categoría: Business
• Categoría: R&D

In today's data-driven world, more sophisticated algorithms for data processing are in high demand, mainly when the data cannot be handled with the help of traditional techniques. Self-learning and adaptive algorithms are now widely used by such leading giants that as Google, Tesla, Microsoft, and Facebook in their projects and applications. In this guide designed for researchers and students of computer science, readers will find a resource for how to apply methods that work on real-life problems to their challenging applications, and a go-to work that makes fuzzy clustering issues and aspects clear. Including research relevant to those studying cybernetics, applied mathematics, statistics, engineering, and bioinformatics who are working in the areas of machine learning, artificial intelligence, complex system modeling and analysis, neural networks, and optimization, this is an ideal read for anyone interested in learning more about the fascinating new developments in machine learning.

CHAPTER 1

REVIEW OF THE PROBLEM AREA

1.1. LEARNING AND SELF-LEARNING PROCEDURES

A learning process always involves a system which can be described by a vector of parameters to be learned

and input data which are a sequence of observations

, where an n-dimensional feature vector gives observation for each object

. We can define a function describing a system’s error by Eq. 1.1 (Tsypkin, 1970):

where

is some predefined objective function and

is the density distribution for

in

.

For a continuous function

, the purpose of learning procedure is to achieve an optimum state for the system

when the functional (Eq. 1.1) attains an extremum value

. Usually, the state

cannot be determined accurately due to the lack of information, as, in general, the distribution density

is also unknown.

If some information about the desired reaction for the system is available for a subset

, it is called a learning set (a training set), and responses

corresponding to each element are called a learning signal (a training signal). Thus the purpose of learning procedure, in this case, is to minimize the differences between a system’s actual output

and desired output

. The objective function

which minimizes the functional (Eq. 1.1) can be defined (in the purest form) as

Analytical or numerical minimization of these objective functions leads to a variety of supervised learning algorithms.

If the training signal

is unavailable, construction of the objective function becomes less trivial. In the most general terms, the self-learning process aims to minimize a divergence between the actual density function p(x) and the approximated one

based on the system’s performance:

Since neither

nor

can be measured directly, it leads to a wide variety of objective functions and algorithms based on these functions.

The main feature of intelligent systems is their ability of learning and self-learning, i.e., the ability to make generalizations based on available and incoming data. This fact allows them to be used for solving problems automatically under specific conditions, such as lack of a priori information about the data nature and the subject area.

Learning procedures can be described in the form of stochastic difference and differential equations for tunable parameters of a system. In some cases, these equations have an exact solution, but numerical methods are commonly used to ensure an asymptotic convergence to an optimal solution. This leads to the fact that most of the learning procedures are iterative.

Most of the learning procedures can be attributed to either of these two basic classes: supervised learning and unsupervised learning (self-learning). In the supervised learning case, the data contain both input information and examples of desired system responses to the input data that make it possible to train the system by comparing its output signal with samples. In case of unsupervised learning, the system has no information about desired outputs, and its task is to detect patterns in a dataset when any data element is not a solution.

1.2. CLUSTERING

Clustering (automatic classification) is one of the primary tasks in data mining, and it implies isolation of similar observations in a dataset in the most general case. In the formal form, the clustering problem is formulated as follows: given a data sample

consisting

observations

where each observation is an n-dimensional feature vector,

. It is often convenient to have a data sample in a matrix form

. These forms are similar.

A solution for the clustering problem is to find a partition matrix

where

stands for an observation’s membership level

to the

–th cluster,

. A general formulation of the problem does not regulate whether some clusters are set beforehand or found by an algorithm.

The feature that differentiates this problem statement from the classification is that no membership tag is specified for a group for any data subset, i.e., clustering is an unsupervised task.

Decision for clustering problems is fundamentally ambiguous. The various reasons for this are as follows:

(1) There is no best or universal quality criterion or objective function for a clustering problem. However, there is a vast number of heuristic criteria, as well as some algorithms without a clearly expressed criterion, and all of them can give different results.

(2) Some clusters are usually previously unknown and are set based on some subjective considerations.

(3) A clustering result strongly depends on a metric which is typically subjective and determined by an expert.

(4) Evaluation of the clustering quality is also subjective.

1.2.1. Clustering Methods

Although there are a lot of clustering approaches, this book mainly focuses on prototype-based methods (Borgelt, 2005; Xu & Wunsch, 2009). These methods select a small number of the most typical (averaged) observations (also called prototypes or centroids) from a sample (or generating data based on it) and divide the rest of the sample into clusters, based on their proximity.

According to the clustering problem statement, the sample should be divided into clusters, with similar observations placed in one cluster, and each cluster differs from the other as much as possible. From a mathematical point of view, this statement can be interpreted as minimizing intra-cluster distances in some metrics. Using prototypes makes it possible to minimize the distance between each observation and each cluster pro...