Logistic Differential Equation

11 Key excerpts on "Logistic Differential Equation"

• 

  eBook - PDF

  Calculus

  Concepts and Contexts, Enhanced Edition

  • James Stewart(Author)
  • 2018(Publication Date)
  • Cengage Learning EMEA

    (Publisher)

  . . Copyright 2019 Cengage Learning. All Rights Reserved. May not be copied, scanned, or duplicated, in whole or in part. Due to electronic rights, some third party content may be suppressed from the eBook and/or eChapter(s). Editorial review has deemed that any suppressed content does not materially affect the overall learning experience. Cengage Learning reserves the right to remove additional content at any time if subsequent rights restrictions require it. SECTION 7.5 THE LOGISTIC EQUATION 537 The table in the margin shows midyear values of , the population of Belgium, in thou-sands, at time , from 1980 to 2000. Figure 6 shows these data points together with a shift-ed logistic function obtained from a calculator with the ability to fit a logistic function to these points by regression. We see that the logistic model provides a very good fit. Other Models for Population Growth The Law of Natural Growth and the Logistic Differential Equation are not the only equa-tions that have been proposed to model population growth. In Exercise 18 we look at the Gompertz growth function and in Exercises 19 and 20 we investigate seasonal-growth models. Two of the other models are modifications of the logistic model. The differential equation has been used to model populations that are subject to “harvesting” of one sort or another. (Think of a population of fish being caught at a constant rate.) This equation is explored in Exercises 15 and 16. For some species there is a minimum population level m below which the species tends to become extinct. (Adults may not be able to find suitable mates.) Such populations have been modeled by the differential equation where the extra factor, , takes into account the consequences of a sparse popula-tion (see Exercise 17).

  Sign up to read

  Learn more about book
• 

  eBook - PDF

  Economic Dynamics with Memory

  Fractional Calculus Approach

  • Vasily E. Tarasov, Valentina V. Podoskina, Valentina V. Tarasova(Authors)
  • 2021(Publication Date)
  • De Gruyter

    (Publisher)

  The logistic map is considered as a discrete analog of this differential equation. The logistic map, which is a simple quadratic map, demon-strates complicated dynamics, which can be characterized as universal and chaotic [343, 260, 27, 511]. The Logistic Differential Equation can be derived from economic model of natural growth in a competitive environment [493, pp. 84–90]. The economic natural growth models are described by equations, in which the rate of change of output is directly proportional to income. In the description of economic growth, the competition effects are taken into account by considering the price as a function of the value of output. Model of natural growth in a competitive environment is often called a model of logis-tic growth. Logistic equation with continuously distributed lag and its application in economics is given in [403]. Natural growth in a competitive environment with mem-ory was first proposed in [444]. 27.2 Logistic growth with memory and periodic kicks To take into account the power-law memory effects in the natural growth model with a competitive environment, we propose [444] the equation https://doi.org/10.1515/9783110627459-027 27.2 Logistic growth with memory and periodic kicks | 475 ( D α C ; 0 + Y )( t ) = m v P ( Y ( t ) ) Y ( t ), (27.1) where ( D α C ; 0 + Y )( t ) is the Caputo derivative (27.2) of the order α ≥ 0 of the function Y ( t ) with respect to time. The left-sided Caputo derivative of order α > 0 is defined by the equation ( D α C ; 0 + Y )( t ) = 1 Γ ( n − α ) t ∫ 0 Y ( n ) ( τ ) dτ ( t − τ ) α − n + 1 , (27.2) where n − 1 < α ≤ n , Γ ( α ) is the gamma function, Y ( n ) ( τ ) is the derivative of the integer order n = [ α ]+ 1 of the function Y ( τ ) with respect to the variable τ : 0 < τ < t . For integer orders α = n , the Caputo derivatives coincide with the standard derivatives of integer orders, i.

  Sign up to read

  Learn more about book
• 

  eBook - PDF

  Calculus: Early Transcendentals, Metric Edition

  • James Stewart, Daniel K. Clegg, Saleem Watson, , James Stewart, James Stewart, Daniel K. Clegg, Saleem Watson(Authors)
  • 2020(Publication Date)
  • Cengage Learning EMEA

    (Publisher)

  FIGURE 5 Logistic model for the population of Japan Copyright 2021 Cengage Learning. All Rights Reserved. May not be copied, scanned, or duplicated, in whole or in part. Due to electronic rights, some third party content may be suppressed from the eBook and/or eChapter(s). Editorial review has deemed that any suppressed content does not materially affect the overall learning experience. Cengage Learning reserves the right to remove additional content at any time if subsequent rights restrictions require it. 638 CHAPTER 9 Differential Equations ■ Other Models for Population Growth The Law of Natural Growth and the Logistic Differential Equation are not the only equa- tions that have been proposed to model population growth. In Exercise 22 we look at the Gompertz growth function and in Exercises 23 and 24 we investigate seasonal-growth models. Two additional models are modifications of the logistic model. The differential equation dP dt - kP S 1 2 P M D 2 c has been used to model populations that are subject to harvesting of one sort or another. (Think of a population of fish being caught at a constant rate.) This equation is explored in Exercises 19 and 20. For some species there is a minimum population level m below which the species tends to become extinct. (Adults may not be able to find suitable mates.) Such popula- tions have been modeled by the differential equation dP dt - kP S 1 2 P M DS 1 2 m P D where the extra factor, 1 2 myP, takes into account the consequences of a sparse popula- tion (see Exercise 21). 9.4 Exercises 1–2 A population grows according to the given logistic equation, where t is measured in weeks. (a) What is the carrying capacity? What is the value of k ? (b) Write the solution of the equation. (c) What is the population after 10 weeks? 1. dP dt - 0.04P S 1 2 P 1200 D , Ps0d - 60 2.

  Sign up to read

  Learn more about book
• 

  eBook - PDF

  Mathematical Modeling in the Social and Life Sciences

  • Michael Olinick(Author)
  • 2014(Publication Date)
  • Wiley

    (Publisher)

  B. Mathematical Analysis The logistic equation may be solved by a nice application of the technique of partial fraction decomposition. The differential equation dP dt = P a − bP IV. Logistic Population Growth 73 may be written in the equivalent form 1 P a − bP dP = 1dt 21 after separating variables and integrating. Now the fraction 1 P a − bP may be decomposed as 1 P a − bP = 1 a P + b a a − bP 22 so that we have the equivalent integration problem 1 P + b a − bP dP = a dt 23 Simple integration then yields log P − log a − bP = at + C 24 where C is a constant of integration. We may rewrite this last equation as log P a − bP = at + C 25 Exponentiation of each side gives P a − bP = Ke at 26 FIGURE 3.5 Direction field for a logistic equation. 0 500 1,000 P(t) 1,500 2,000 100 50 t 150 200 74 CHAPTER 3 Ecological Models: Single Species where K is the constant e C . It is useful to rewrite this equation as P = aKe at 1 + bKe at = a b + 1 + K e − at = a b 1 + 1 bK e − at = k 1 + e d − at 27 where d = log bK and k = a b. Since a is positive, e at tends to 0 as t increases. Thus, lim t→∞ P t = k = a b. The logistic model then predicts that population will increase and asymptotically approach the carrying capacity a b. Note that at the capacity level of P = a b, the logistic equation gives dP dt = 0. See Fig. 3.6 for a graph of the population as a function of time. This curve is called the logistic curve, and resembles an elongated letter S. Another useful way to examine logistic growth comes if we make the change of variable Q = b a P in the differential equation dP dt = P a − b P. We can interpret Q t as the fraction of the carrying capacity the population has reached at time t , since Q = 0 when P = 0 and Q = 1 when P = a b , the carrying capacity. Then we have dQ dt = b a dP dt = b a P a − bP = Q a − aQ = aQ 1 − Q . or, more simply, dQ dt = aQ 1 − Q 28 It is straightforward to show that Q t = 1 1 + Ce − at where the constant C is equal to 1 Q 0 − 1.

  Sign up to read

  Learn more about book
• 

  eBook - PDF

  Modeling Differential Equations in Biology

  • Clifford Henry Taubes(Author)
  • 2008(Publication Date)
  • Cambridge University Press

    (Publisher)

  (This last discussion paraphrases material from Berger, A., ed., Climatic. Variations and Variability, D. Reidel, Dordrecht.) 3.6 Lessons Here are some key ideas from this chapter: • The logistic equation is commonly used to model population growth in a resource- limited environment. • The qualitive behavior of solutions p(t) to the logistic equation, and to the generic equation J7P = /(/?)> c a n t> e obtained from information in the graph of the function / . • The points where the graph crosses the p-axis correspond to constant solutions to the differential equation. Meanwhile, if p(t) is a time dependent solution and f(p(t)) > 0, then p(t) moves to the right on the p-axis as time increases. Conversely, if f(p(t)) < 0, then p(t) moves to the left. • An equation of the form j- t p = f(p) is completely predictive. Choose any starting value for p and there is precisely one solution that starts at your chosen starting time with your chosen starting value. READINGS FOR CHAPTER 3 READING 3.1 Biologists Sort the Lessons of Fisheries Collapse Commentary: The purpose of this article is to illustrate the complicated issues that arise when biology collides with economics. The point of the article is that many oceanfisheriesare in dire straights, that these dire straights were more or less predicted by scientists, but that the scientific predictions were not well received by the fishing industry. Scientists argued that if there is uncertainty in the predictions (which there almost always is), then one should err on the side of the resource—fish. Thus, cut back on fishing to decrease mortality. Meanwhile, the industry has argued that you should err on the side of economics and thefishingindustry's short-term interests. The industry's voice tends to carry more weight on the relevant councils. Readings for Chapter 3 53 Biologists Sort the Lessons of Fisheries Collapse Science, 264 (1994) 1252-1253.

  Sign up to read

  Learn more about book
• 

  eBook - PDF

  Population Dynamics

  Alternative Models

  • Bertram G. Jr. Murray(Author)
  • 2013(Publication Date)
  • Academic Press

    (Publisher)

  Mathematical analysis of populations is essential for developing an understanding of population processes, and, although idealized models are simpler than the natural phenomena they intend to describe, they are useful for organizing data and thoughts and for providing insights. Idealized mathematical models are often unappreciated by field ecologists, but Bartlett (1973) correctly asked, Until we can understand the proper-ties of these simple models, how can we begin to understand the more complicated real situation? This book is a field ecologist's attempt to discover quantitative relation-ships between population parameters in order to understand the observ-able world and perhaps to serve as an antidote to the recent trend toward mathematical elegance (e.g., May, 1976b; Pielou, 1977). For the field biologist, mathematics is no more than a tool, and the minimal set of tools falls into three distinct categories: (1) the exponential and logistic equations describing population growth (Verhulst, 1838; Pearl and Reed, 1920), (2) actuarial equations relating several population parameters (Lotka, 1925), and (3) the projection matrix (Leslie, 1945, 1948). These will be considered only to the extent necessary to follow the theoretical de-velopment in later chapters. Fuller treatment of population mathematics can be found in Pielou (1969, 1977), Mertz (1970), and Poole (1974). E X P O N E N T I A L AND LOGISTIC EQUATIONS 19 E PONENTIA LAN DLOGISTI CE ATION S The dynamics of population growth has been described most frequently by exponential and logistic equations (Verhulst, 1838; Pearl and Reed, 1920). These describe the change in numbers of populations in unlimited and limited situations, respectively. In constant and unlimited conditions, the rate of change in population size is given by dN ~dT = rN > ( 2 J ) where r is the instantaneous rate of increase per head and is the population's size.

  Sign up to read

  Learn more about book
• 

  eBook - PDF

  The Theoretical Biologist's Toolbox

  Quantitative Methods for Ecology and Evolutionary Biology

  • Marc Mangel(Author)
  • 2006(Publication Date)
  • Cambridge University Press

    (Publisher)

  The discrete logistic map and the edge of chaos We now come to what must be one of the most remarkable stories of good luck and good sleuthing in science. To begin this story, 38 Topics from ordinary and partial differential equations I encourage you to stop reading just now, go to a computer and plot the trajectories for N ( t ) given by the formula for N ( t ) in the previous exercise, for a variety of values of r – let r range from 0.4 to about 3.5. After that return to this reading. Now let us poke around a bit with the logistic equation by recogniz-ing the definition of the derivative as a limiting process. Thus, we could rewrite the logistic equation in the following form: lim d t ! 0 N ð t þ d t Þ N ð t Þ d t ¼ rN 1 N K (2 : 28) This equation, of course, is no different from our starting point. But now let us ignore the limiting process in Eq. ( 2.28 ) and simply set d t ¼ 1. If we do that Eq. ( 2.28 ) becomes a difference equation, which we can write in the form N ð t þ 1 Þ ¼ N ð t Þ þ rN ð t Þ 1 N ð t Þ K (2 : 29) This equation is called the logistic map, because it ‘‘maps’’ population size at one time to population size at another time. You may also see it written in the form N ð t þ 1 Þ ¼ rN ð t Þ 1 N ð t Þ K which makes it harder to connect to the original differential equation. Note, of course, that Eq. ( 2.29 ) is a perfectly good starting point, if we think that the biology operates in discrete time (e.g. insect populations with non-overlapping generations across seasons, or many species of fish in temperate or colder waters). Although Eq. ( 2.29 ) looks like the Logistic Differential Equation, it has a number of properties that are sufficiently different to make us wonder about it.

  Sign up to read

  Learn more about book
• 

  eBook - PDF

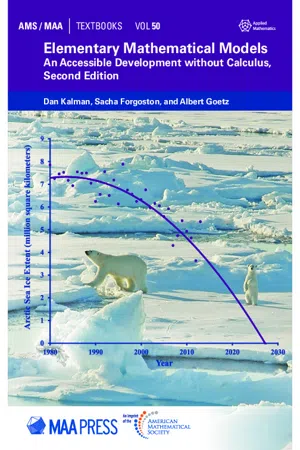
  Elementary Mathematical Models

  An Accessible Development without Calculus, Second Edition

  • Dan Kalman, Sacha Forgoston, Albert Goetz(Authors)
  • 2019(Publication Date)
  • American Mathematical Society

    (Publisher)

  6 Logistic Growth In Chapter 4 we considered population models based on geometric growth sequences. Typically in such a model the terms ? 0 , ? 1 , ? 2 , etc., represent population sizes at reg-ularly spaced time intervals, for example, every day, every month, or every year. The geometric growth assumption is that each successive term increases or decreases by an equal percentage, or equivalently, by an equal growth factor ? , over the preceding term. Under this assumption, the functional equation is ? 𝑛 = ? 0 ? 𝑛 . And when ? > 1 this function grows exponentially. Thus the model predicts that the population will grow at an ever increasing pace, without any upper limit. In practical terms we know that this type of model must be unrealistic in the long term. Certainly, for biological populations, exponential growth cannot continue in-definitely. Competition for resources must eventually restrict population growth. But even outside of biology, it is difficult to imagine a context where unrestricted growth is a practical possibility. In this chapter we introduce more realistic models that represent limited popula-tion growth . They assume not a constant growth factor, but rather a growth factor that gets smaller as the population grows larger. As a first specific instance of this idea, we assume that the growth factor decreases linearly as a population increases. That leads to a family of models we refer to as logistic growth . 1 Logistic growth sequences will be defined and analyzed in Section 6.1. As in past chapters we will discuss common properties of these models, including difference equations and graphs. As we will see, in many cases logistic growth sequences agree with our expectations about how a population should grow, subject to limited resources. On the other hand, logistic sequences differ in important ways from the sequences we have seen in earlier chapters.

  Sign up to read

  Learn more about book
• 

  eBook - PDF

  Dynamical Systems for Biological Modeling

  An Introduction

  • Fred Brauer, Christopher Kribs(Authors)
  • 2015(Publication Date)
  • Chapman and Hall/CRC

    (Publisher)

  5–6. First-Order Differential Equations (Continuous Dynamical Systems) 109 with c a constant of integration; in fact, c = y (0) + ax (0). Now, substitution of (3.11) into (3.10) gives y ′ ( t ) = bx ( t ) y ( t ) = b parenleftbigg c − y ( t ) a parenrightbigg y ( t ) = bc a y ( t ) parenleftBig 1 − y ( t ) c parenrightBig . We now let r = bc/a , K = c , and we obtain the Logistic Differential Equation (3.8) for the total biomass of the population. We again consider r to be the maximum intrinsic per capita growth rate (in units of per time) and K to be the carrying capacity determined by the resources of the environment and the needs of the population. This equation was originally proposed by Verhulst 4 to model the assump-tion that the per capita growth rate should decrease as population size in-creases. Verhulst chose a decreasing linear function as the per capita growth rate for simplicity. Solutions of the logistic equation have been fitted to many different population models with considerable predictive success; although the notion of biomass may make one think of simple organisms, Verhulst’s original application was to humans. In Section 3.4, we will show how to solve the Logistic Differential Equation (3.8) explicitly, using a technique called separation of variables. For now, we may verify that for every constant c the function y = K 1 + ce − rt (3.12) is a solution of this differential equation. 5 To see this, note that for the given function y , y ′ = Kcr e − rt (1 + ce − rt ) 2 and 1 − y K = K − y K = ce − rt (1 + ce − rt ) . Thus ry parenleftBig 1 − y K parenrightBig = Krc e − rt (1 + ce − rt ) 2 = y ′ , and the given function satisfies the Logistic Differential Equation for every choice of c . 4 P.F. Verhulst, Notice sur la loi que la population suit dans son accroissement, Corr.

  Sign up to read

  Learn more about book
• 

  eBook - PDF

  Calculus

  Single Variable

  • Deborah Hughes-Hallett, Andrew M. Gleason, William G. McCallum, Daniel E. Flath, Patti Frazer Lock, David O. Lomen, David Lovelock, Brad G. Osgood, Douglas Quinney, Karen R. Rhea, Jeff Tecosky-Feldman, Thomas W. Tucker, Otto K. Bretscher, Sheldon P. Gordon, Andrew Pasquale, Joseph Thrash(Authors)
  • 2014(Publication Date)
  • Wiley

    (Publisher)

  For example, when a June 8, 2007 decision by the Delaware Superior Court in- validated a two-year moratorium on catching horseshoe crabs, the Delaware Department of Natural Resources and Environmental Control imposed instead an annual quota of 100,000 on male horseshoe crabs. Environmen- talists argued this would exacerbate a decrease in the pro- tected Red Knot bird population that depends on the crab for food. For a population P that satisfies the logistic model with harvesting, dP dt = kP  1 - P L  - H, show that the quota, H, must satisfy H ≤ kL/4, or else the population P may die out. (In fact, H should be kept much less than kL/4 to be safe.) 11.8 SYSTEMS OF DIFFERENTIAL EQUATIONS 657 39. A Logistic model with Threshold. We want to model a population P (t) as a function of time using a differential equation model. We want our model to have all the fol- lowing properties: 1. If the population is 0 at any time, it remains at 0; 2. If the population is below a certain fixed threshold A, then it goes down towards 0 asymptotically; 3. If the population is above this same threshold A and below a limiting capacity L, then it grows asymptotically towards L; 4. If the population starts out above L, it decays asymp- totically towards L. Can you think up one such model? Strengthen Your Understanding In Problems 40–42, explain what is wrong with the statement. 40. The differential equation dP/dt = 0.08P - 0.0032P 2 has one equilibrium solution, at P = 25. 41. The maximum rate of change occurs at t = 25 for a quantity Q growing according to the logistic equation dQ dt = 0.13Q(1 - 0.02Q). 42. Figure 11.75 shows a quantity growing logistically. 60 100 t P Figure 11.75 In Problems 43–46, give an example of: 43. A quantity that increases logistically. 44. A Logistic Differential Equation for a quantity P such that the maximum rate of change of P occurs when P = 75. 45. A graph of dQ/dt against Q if Q is growing logistically and has an equilibrium value at Q = 500.

  Sign up to read

  Learn more about book
• 

  eBook - PDF

  Calculus of a Single Variable: Early Transcendental Functions, International Metric Edition

  • Ron Larson, Bruce Edwards(Authors)
  • 2018(Publication Date)
  • Cengage Learning EMEA

    (Publisher)

  You observed that the differential equation dyH20862dt = ky has the general solution y = Ce kt . Exponential growth is unlimited, but when describing a population, there often exists some upper limit L past which growth cannot occur. This upper limit L is called the carrying capacity, which is the maximum population y(t) that can be sustained or supported as time t increases. A model that is often used to describe this type of growth is the Logistic Differential Equation dy dt = ky parenleft.alt4 1 - y L parenright.alt4 Logistic Differential Equation where k and L are positive constants. A population that satisfies this equation does not grow without bound, but approaches the carrying capacity L as t increases. From the equation, you can see that if y is between 0 and the carrying capacity L, then dyH20862dt > 0, and the population increases. If y is greater than L, then dyH20862dt < 0, and the population decreases. The general solution of the Logistic Differential Equation is derived in the next example. Deriving the General Solution Solve the Logistic Differential Equation dy dt = ky parenleft.alt4 1 - y L parenright.alt4 . Solution Begin by separating variables. dy dt = ky parenleft.alt4 1 - y L parenright.alt4 Write differential equation. 1 y(1 - yH20862L) dy = k dt Separate variables. integral.alt1 1 y(1 - yH20862L) dy = integral.alt1 k dt Integrate each side. integral.alt1 parenleft.alt4 1 y + 1 L - y parenright.alt4 dy = integral.alt1 k dt Rewrite left side using partial fractions. ln uni2223 y uni2223 - ln uni2223 L - y uni2223 = kt + C Find antiderivative of each side. ln uni2223 L - y y uni2223 = -kt - C Multiply each side by -1 and simplify. uni2223 L - y y uni2223 = e -kt -C Exponentiate each side. uni2223 L - y y uni2223 = e -C e -kt Property of exponents L - y y = be -kt Let ±e -C = b. Solving this equation for y produces the general solution y = L 1 + be -kt . REMARK A review of the method of partial fractions is given in Section 8.5.

  Sign up to read

  Learn more about book