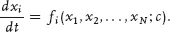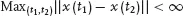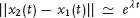![]()
Chapter 1
Introduction
The subject of this book is chaos as seen through the filter of topology. The origin of this book lies in the analysis of data generated by a dynamical system operating in a chaotic regime. Throughout this book we develop topological tools for analyzing chaotic data and then show how they are applied to experimental data sets.
More specifically, we describe how to extract, from chaotic data, topological signatures that determine the stretching and squeezing mechanisms that act on flows in phase space and that are responsible for generating chaotic data.
In the first section of this introductory chapter we very briefly review some of the basic ideas from the field of nonlinear dynamics and chaos. This is done to make the work as self-contained as possible. More in-depth treatment of these ideas can be found in the references provided.
In the second section we describe, for purposes of motivation, a laser that has been operated under conditions in which it behaved chaotically. The topological methods of analysis that we describe in this book were developed in response to the challenge of analyzing chaotic data sets generated by this laser.
In the third section we list a number of questions we would like to be able to answer when analyzing a chaotic signal. None of these questions can be addressed by the older tools for analyzing chaotic data. The older methods involve estimates of the spectrum of Lyapunov exponents and estimates of the spectrum of fractal dimensions. The question that we would particularly like to be able to answer is this: How does one model the dynamics? To answer this question we must determine the stretching and squeezing mechanisms that operate together – repeatedly – to generate chaotic data. The stretching mechanism is responsible for sensitivity to initial conditions while the squeezing mechanism is responsible for recurrent nonperiodic behavior. These two mechanisms operate repeatedly to generate a strange attractor with a self-similar structure.
A new analysis method, topological analysis, has been developed to respond to the fundamental question just stated [7, 8]. At the present time this method is suitable only for strange attractors that can be embedded in three-dimensional spaces. However, for such strange attractors it offers a complete and satisfying resolution to this question. The results are previewed in the fourth section of this chapter. In the final section we provide a brief overview of the organization of this book. In particular, we summarize the organization and content of the following chapters.
It is astonishing that the topological analysis tools that we describe have provided answers to more questions than we had originally asked. This analysis procedure has also raised more questions than we have answered. We hope that the interaction between experiment and theory and between old questions answered and new questions raised will hasten the evolution of the field of nonlinear dynamics.
1.1 Brief Review of Useful Concepts
There are a number of texts that can serve as excellent introductions to the study of nonlinear dynamics and chaos. These include [9–21]. Any one of these can be used to fill in details that we may pass by a little too quickly in our study. There are also many texts that serve as introductions to topology. All cover far more material than we use here. As a result, we do not recommend that a reader invest time in any one of these texts. We will introduce the topological concepts as needed as we proceed.
For now we review very briefly some of the foundational ideas of chaos.
What Is chaos? We take the following as a useful definition for chaos, or chaotic motion. Chaos is motion that is
1. deterministic
2. bounded
3. nonperiodic
4. sensitive to initial conditions.
Where does this motion take place? It is useful to describe the state of a physical system by a set of coordinates. The most convenient way to do this is to establish a phase space. A point in the phase space describes the state of the physical system. The “motion” described above is that of a point in the phase space. For example, the phase space needed to describe the motion of two particles in a plane is eight-dimensional: two coordinates and two velocity components are required to describe the state of each particle’s motion. We will work with smaller phase spaces.
What is “deterministic motion”? The motion of the coordinates xi of a point in an N-dimensional phase space is governed by a set of N first-order ordinary differential equations:
The coordinates
xRN are called
phase space coordinates and the coordinates
c RK are called
control parameters. A set of
N equations of this type is called a
dynamical system.
What is “bounded” motion? The trajectory defined by the equations of motion
(1.1) can be parameterized by the time coordinate:
x(
t).
Bounded means that the maximum distance between any two points on the trajectory over all times is less than infinity:
.
What is periodic motion? This is motion that returns to its starting point after an elapsed time T: x(t) = x(t + T), for some T > 0. T is called the period if there is no smaller positive value (for example, T/2) for which this equation is true.
What is “sensitivity to initial conditions”? A point
x1 in phase space can serve as an initial condition for a trajectory through it:
x1(
t). Two nearby points can serve as initial conditions for two trajectories, one starting at each point. At first the two trajectories remain close to each other. If the distance between them grows exponentially with time,
with
λ > 0, then the system is said to exhibit sensitivity to initial conditions. This means that, although the evolution is deterministic, the future position of an initial condition becomes unpredictable after some time. The term λ is called a
Lyapunov exponent.
How do you visualize chaotic motion? A very convenient way to do this is to view the trajectory of an initial condition in the phase space. It often happens that the trajectory “wanders around” in the phase space until it “settles down” onto, or is “attracted to,” a reasonably well-defined structure. This structure, when it exists, is called by mathematicians an Ω limit set and by physicists a strange attractor or a chaotic attractor. Plots of strange attractors appear liberally throughout this work: for example, see Figures 6.10 and 7.6.
A strange attractor contains no periodic orbits. However, buried in the strange attractor lies a host of unstable periodic orbits. It is these orbits that form the foundation of the topological analysis methods that are presented in this work. Good approximates to these orbits can be extracted from experimental data.
How do you search for chaotic behavior? A simple, very effective way to do this is to study the motion at a sequence of values of some control parameter. A suitable tool is called a bifurcation diagram. This amounts to a plot of one of the phase space coordinates as a function of one of the control parameters. Phase space plots of the logistic map x′ = λx(1 – x) are presented in Figures 2.3 and 2.4. A practiced eye (training time ∼ 2s) can easily distinguish chaotic from nonchaotic behavior.
Is there a “smoking gun” for chaotic behavior? No. The original discovery [22] that launched a thousand studies was that a period-doubling cascade was a prelude to chaos and that a number of invariants were associated with such cascades (see Preface). The possibility of confirming these predictions, or showing that they were not correct, attracted a number of experimentalists into this field (cf. (10.]). Having said that, not all “routes to chaos” go by the period-doubling pathway.
What topological tools will be used? We will study how the unstable periodic orbits that exist in plenty in a strange attractor are organized. To do this we will rely on the Gauss linking number of a pair of closed orbits as well as a closely related idea (relative rotation rates). We will also study braids and introduce cardboard-type structures that serve to hold all the periodic orbits in a strange attractor in a very simple way. Toward the end of this work we will introduce more venerable topological ideas: E...