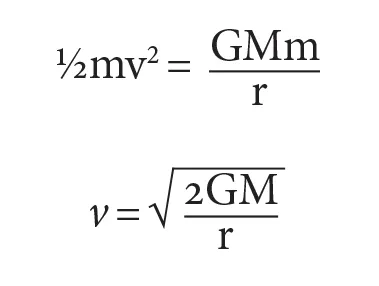Viaggio al centro del Sole

Storia e segreti della nostra stella

Lucie Green

• Editore: Il Saggiatore
• Anno: 2018
• eBook ISBN: 9788865766200
• Argomento: Scienze fisiche
• Categoria: Astronomia e astrofisica

Guardatevi attorno. Tutto quello che vedete esiste esclusivamente grazie a una tra i miliardi e miliardi di stelle che compongono l'Universo: il Sole. Senza il Sole non ci sarebbero la luce, il calore, la gravità e, in definitiva, la vita. Ma che cosa rende questo astro tanto speciale? Che cosa rende possibile quello che è stato impossibile in qualunque altro luogo – per quanto ne sappiamo – nelle infinite profondità del cosmo? In quale modo una potenza capace di originare venti che viaggiano a centinaia di chilometri al secondo riesce a mantenere in equilibrio la Terra e i pianeti e satelliti vicini senza disintegrarli o abbandonarli a un'eterna deriva interspaziale? Viaggio al centro del Sole ci consente di esplorare tutti i segreti della nostra stella madre: dai 170000 anni che un fotone impiega per arrivare all'esterno dal centro del Sole, agli 8 minuti e 20 secondi che gli sono necessari per raggiungere la crosta terrestre; dalle macchie solari, studiate già da Galileo, agli imprevedibili e fugaci «brillamenti», uno sprigionamento di energia pari a quello di 170 milioni di bombe atomiche cui dobbiamo alcune delle più spettacolari aurore dei nostri cieli; dalle teorie sull'origine del Sole fino alle ipotesi su ciò che avverrà alla sua morte, tra circa 5 miliardi di anni. Un racconto che ripercorre i millenni di osservazioni a occhio nudo, i secoli di osservazioni al telescopio e i decenni di osservazioni dallo spazio; le storie degli scopritori dei misteri dell'energia – tra i quali figura anche l'insospettabile medico di bordo di una nave – e dei pionieri dell'esplorazione del cosmo. Con Viaggio al centro del Sole la fisica Lucie Green, grazie a una prosa di rara chiarezza e alla sua profonda competenza scientifica, ci guida attraverso il tempo e la materia a vedere da vicino le tempeste geomagnetiche, le eruzioni sulla superficie del Sole, e ancora oltre – fino a sfiorare con la mente un nucleo che arde a più di 15 milioni di gradi.

12. Espulsioni di massa coronale

Le «espulsioni di massa coronale» (anche indicate come cme, coronal mass ejections) sono le eruzioni più vaste e massicce dell’intero Sistema Solare, eventi in cui fino a 10 miliardi di tonnellate di plasma sono espulse dal Sole a milioni di chilometri all’ora. All’inizio possono essere relativamente piccole, delle dimensioni di un gruppo di macchie solari. Tuttavia, quando il materiale lascia la nostra stella, si espandono fino a diventare diverse volte più grandi del Sole stesso. Sono al di là di qualsiasi immaginazione. Eppure, nonostante la loro maestosità, hanno un nome piuttosto arzigogolato, seppure descrittivo. Si tratta, in effetti, di espulsioni di massa dalla corona del Sole, e purtroppo anche l’acronimo cme non è neanche lontanamente accattivante quanto i nomi dei suoi parenti più prossimi, i «brillamenti solari» o il «vento solare».

Sarebbe stato meglio qualcosa come «eruzioni solari»; mi sarei anche accontentata di «esplosioni solari». E invece no, si chiamano cme, il che può, in un certo senso, indurre a reputarle poco interessanti e a passare oltre.

Lasciando da parte la nomenclatura, attorno alle espulsioni di massa coronale aleggia un mistero ancora più grande di quello relativo alla scelta del loro nome: perché, fino agli anni settanta, qualcosa che si ingigantisce a tal punto è passato del tutto inosservato? Oscurità per mancanza di plausibilità, forse. Con il senno di poi, notiamo che gli indizi erano ben riconoscibili e possiamo asserire che, per secoli, le cme sono state nascoste in bella vista.

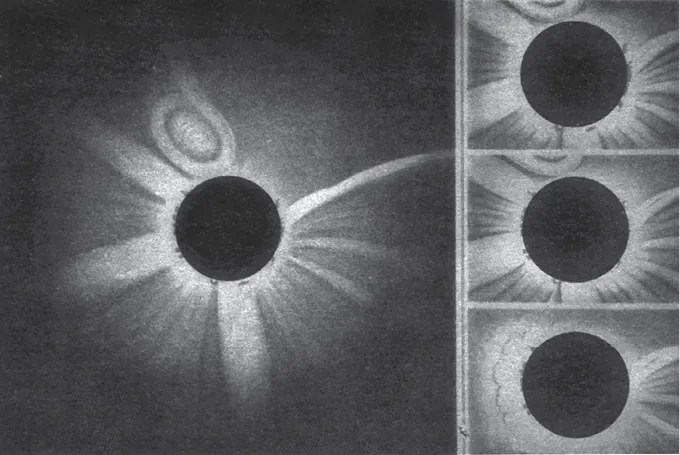
Osserviamo, per esempio, i disegni tracciati durante l’eclissi solare del 1860: ecco che si scorge quella che, quasi certamente, era un’espulsione di massa coronale in fuga dal Sole. Una struttura dalla forma circolare, che spicca rispetto alle altre formazioni radiali chiamate getti coronali. Con l’avvento dello spettroeliografo, la luce emessa nella linea idrogeno-alfa ha mostrato che il plasma della corona formava in effetti strutture che di tanto in tanto eruttavano verso l’alto. Ma al tempo si assumeva che quel materiale non lasciasse mai il Sole.

12.1 Disegni dell’eclissi totale di Sole del 1860, di Wilhelm Tempel (per gentile concessione della Royal Astronomical Society).

L’idea che il plasma venisse espulso in quel modo e viaggiasse nel Sistema Solare era talmente inconcepibile che, nel programmare le missioni Apollo verso la Luna, la nasa non prese assolutamente in considerazione nulla del genere. Gli scienziati si preoccuparono solo delle particelle ad alta energia legate in qualche modo ai brillamenti solari. Non avevano idea che, quando si fanno strada nel Sistema Solare, anche le espulsioni di massa coronale possono creare una pioggia delle stesse particelle.

Solo nel 1971 aprimmo infine gli occhi e osservammo per la prima volta un’espulsione di massa coronale. Le immagini scattate il 13 e il 14 dicembre dall’Orbiting Solar Observatory 7 della nasa mostrarono una sezione della corona che si staccava letteralmente dal Sole. In un primo momento i tecnici pensarono che si trattasse di un problema con la fotocamera, ma presto capirono che stavano osservando un evento reale. Nel 1973 il capo della sezione di fisica solare, Richard Tousey, la stessa persona che per la prima volta aveva registrato da un razzo lo spettro ultravioletto del Sole, pubblicò quanto era stato osservato, e iniziò così l’era delle cme.

È proprio in quest’epoca, immensamente significativa ed emozionante, che ho iniziato a occuparmi di fisica solare. Il vecchio approccio che consisteva nell’usare le eclissi di Sole per osservare la corona aveva ora trovato uno scopo nuovo, e noi una nuova sfida: scoprire le origini dell’energia che alimenta queste eruzioni enormi. Lungo la strada abbiamo scoperto che ci raccontano qualcosa di veramente speciale sul campo magnetico solare. È molto più dinamico di quanto non avessimo mai potuto immaginare e, di tanto in tanto, si comporta come una pentola a pressione pronta a esplodere.

Montagne volanti

All’inizio del capitolo ho detto che un’espulsione di massa coronale coinvolge una quantità di materiale solare enorme, fino a 10 milioni di tonnellate di plasma. Si tratta di un’affermazione importante, che posso tuttavia fare con certezza perché, dato il modo in cui osserviamo l’eruzione, possiamo calcolare la massa del materiale eiettato.

Come abbiamo detto, la corona è osservabile nel campo della luce visibile solo durante un’eclissi di Sole totale. Il gesto di bloccare la luce della fotosfera svela la corona perché gli elettroni nel plasma coronale diffondono la luce fotosferica. La corona diventa debolmente visibile perché i suoi elettroni fanno sì che venga di fatto «accesa» dalla luce proveniente dal basso. Oggi alcuni telescopi spaziali montano un disco che fa le veci della Luna e genera un’«eclissi artificiale», ma il processo impiegato per osservare la corona è esattamente lo stesso. Quando vediamo le immagini di un’espulsione di massa coronale stiamo dunque osservando la luce diffusa dagli elettroni nel suo plasma. Sappiamo che devono essere accompagnati da protoni e altre particelle, ma questa tecnica non ne rivela la presenza.

Possiamo però calcolare quanti dovrebbero essere. La luminosità dell’espulsione di massa coronale nella luce visibile diffusa ci permette di calcolare il numero di elettroni. Ci resta dunque solo da stabilire quante particelle di tipo diverso ci sono per ogni elettrone; da questo dato ricaviamo la massa totale dell’espulsione.

Se tralasciamo gli elementi in tracce, presenti solo in quantità minuscole, circa il 10 per cento delle particelle del plasma coronale è composto da elio e il 90 per cento da idrogeno. Quindi, per ogni particella di elio ci sono nove particelle di idrogeno. Un atomo di idrogeno possiede un elettrone, mentre un atomo di elio ne ha due, e tutti, essendo stati strappati ai loro nuclei, sono liberi di circolare nel plasma. Il rapporto di nove idrogeni per ogni elio ci fornisce pertanto un totale di undici elettroni. I nuclei di elio contengono due protoni e due neutroni, mentre quelli di idrogeno sono composti da un singolo protone. Detto fatto: ogni undici elettroni osservati, devono esserci in giro undici protoni e due neutroni.

È importante tenerne conto perché, nonostante siano gli elettroni a mostrarsi diffondendo i fotoni, sono i protoni e i neutroni a determinare la massa della cme. La massa di un elettrone è nulla se confrontata con quella delle altre particelle. La massa di un protone è di 1,6726 × 10–24 grammi e quella di un neutrone di 1,6749 × 10–24 grammi. Quella di un elettrone è più piccola di circa tre ordini di grandezza. Sommate questi valori e scoprirete che la massa di plasma presente nell’espulsione è immensa: tra i 10 milioni e i 10 miliardi di tonnellate di materiale, circa la stessa massa del monte Everest.

Si capisce facilmente perché le espulsioni di massa coronale furono ritenute inverosimili: pensate a quanta energia serve per staccare via dal Sole qualcosa di grande quanto il monte Everest. È solamente una piccola percentuale della massa che il Sole perde quotidianamente a causa del vento solare (che trasporta un milione di tonnellate al secondo), nonché una frazione trascurabile della massa totale del Sole. Tuttavia, l’enorme attrazione gravitazionale della nostra stella implica che debba accadere qualcosa di straordinario affinché la massa dell’espulsione possa staccarsi tutta in un colpo solo. Non riesco nemmeno a immaginare una tale quantità di materiale partire dalla Terra. E se invece si trattasse di qualcosa di più piccolo?

In altre parole, che cosa ci vorrebbe affinché un oggetto di dimensioni relativamente ridotte, per esempio una pallina da tennis, lasci la Terra e non vi faccia più ritorno? Dall’esperienza quotidiana sappiamo che un oggetto arriva tanto più in alto quanto più veloce è stato scagliato. Eppure, non importa quanto ci impegniamo, man mano che la pallina sale, rallenta per poi ricadere a terra. Ma, in teoria, qualcuno con una forza sovraumana potrebbe lanciare la pallina abbastanza velocemente da permetterle di liberarsi dalla morsa gravitazionale terrestre? Se ragioniamo in termini di energia, è necessario fornire alla palla un’energia cinetica, ossia dovuta al moto, tale da eccedere la sua energia potenziale gravitazionale sulla superficie terrestre. Dobbiamo calcolare la velocità di fuga della pallina.

Ce la caviamo con un paio di equazioni: l’energia cinetica* della pallina, e in effetti di qualsiasi oggetto, dipende dalla sua massa e dal quadrato della sua velocità; la sua energia potenziale gravitazionale** è invece data dalla massa della pallina moltiplicata per la massa della Terra e la costante di gravitazione universale, il tutto diviso per la distanza tra la pallina e il centro della Terra, ossia il raggio terrestre.

Come in qualsiasi problema di algebra che si rispetti, la massa della pallina appare in entrambe le formule, quindi la possiamo semplificare. I fattori importanti per ricavare la velocità di fuga sono la massa della Terra e la distanza della pallina dal centro del nostro pianeta. La massa della pallina non entra in gioco. La velocità di fuga è la stessa per qualsiasi oggetto che deve lasciare la Terra, che si tratti di una pallina da tennis o di una palla di cannone.

La velocità di fuga è pari a circa 40 000 chilometri all’ora. Se trascuriamo la resistenza prodotta dall’aria circostante, per fuggire dalla morsa della gravità terrestre la pallina dovrebbe percorrere 11,2 chilometri ogni secondo. Possiamo dunque seguire la stessa logica per ricavare la velocità di fuga dal Sole: è sufficiente riscalare dimensioni e massa.

Il Sole è enorme, oltre ogni immaginazione. Abbiamo forse un’idea abbastanza precisa di quanto possa essere grande la nostra città, e una un po’ più vaga della grandezza dello stato in cui viviamo, ma già le dimensioni dell’intera Terra vanno oltre quanto il nostro cervello possa intuitivamente concepire. Ebbene: dentro il Sole riusciremmo a far entrare comodamente oltre un milione di Terre. Prendete un milione di quelle cose troppo grandi per essere comprese intuitivamente e avrete le dimensioni del Sole. Anche la sua massa è enorme, al punto da generare un’attrazione gravitazionale a livello della fotosfera ben ventisette volte maggiore della forza di gravità che percepiamo sulla terraferma.

Ovviamente, problemi ben maggiori della gravità ci tengono lontani dalla fotosfera solare. Ma anche immaginando per assurdo che il Sole avesse una superficie fresca e abitabile, 27g non sarebbero uno scherzo.*** Quei 100 grammi di patatine di mais che abbiamo mangiato qualche capitolo fa verrebbero tirati verso il centro del Sole con una forza pari a quella subita da 2,7 chilogrammi qui sulla Terra. E una normale persona di 75 chilogrammi peserebbe sulla superficie del Sole l’equivalente di oltre 2 tonnellate. Come se non bastasse, sopportare una forza gravitazionale pari anche solo a 10g è fatale per l’uomo: con 27g non saremmo in condizione di godere a lungo della nostra vacanza.

La massa d...

Indice dei contenuti

• Copertina
• Sommario
• Introduzione
• La luce: da non credere ai propri occhi
• L'energia delle stelle
• Una grande famiglia
• La vita segreta di un fotone
• Macchie sul sole
• La rotazione: l’attacco del Sole
• Il Sole dinamico
• Eclissi e arcobaleni
• Bon voyage
• L’era dei viaggi spaziali
• I brillamenti solari
• Espulsioni di massa coronale
• Vivere nell’atmosfera del Sole
• Che cosa ci aspetta?
• Conclusioni
• Appendice
• Ringraziamenti
• Glossario
• Bibliografia
• Inserto fotografico