Number Theory and Its History

Oystein Ore

• Editore: Dover Publications
• Anno: 2012
• ISBN:
  9780486136431
• Argomento: Matematica
• Categoria: Teoria dei numeri

Unusually clear, accessible introduction covers counting, properties of numbers, prime numbers, Aliquot parts, Diophantine problems, congruences, much more. Bibliography.

CHAPTER 1

COUNTING AND RECORDING OF NUMBERS

1–1. Numbers and counting

All the various forms of human culture and human society, even the most rudimentary types, seem to require some concept of number and some process for counting. According to the anthropologists, every people has some terminology for the first numbers, although in the most primitive tribes this may not extend beyond two or three. In a general way one can say that the process of counting consists in matching the objects to be counted with some familiar set of objects like fingers, toes, pebbles, sticks, notches, or the number words. It may be observed that the counting process often goes considerably beyond the existing terms for numerals in the language.

1–2. Basic number groups.

Almost all people seem to have used their fingers as the most convenient and natural counters. In many languages this is easily recognized in the number terminology. In English we still use the term digits for the numerals. For numbers exceeding 10 the toes have quite commonly been used as further counters.

Very early in the cultural development it became necessary to perform more extensive counts to determine the number of cattle, of friends and foes, of days and years, and so on. To handle larger figures the counting process must be systematized. The first step in this direction consists in arranging the numbers into convenient groups. The choice of such basic groups depends naturally on the matching process used in counting.

The great preponderance of people use a basic decimal or decadic group of 10 objects, as one should expect from counting on the fingers. The word for 10 often signifies one man. Quinary systems based on groups of 5 or one hand also occur, but the vigesimal systems based on a 20 group are much more common, corresponding of course to a complete count of fingers and toes. Among the American Indian peoples the vigesimal system was in widespread use; best known is the well-developed Mayan system. One finds traces of a 20 system in many other languages. We still count in scores. The French quatre-vingt for 80 is a remnant of a previously more extensive 20 count. In Danish the 20 system is still used systematically for the names of numbers less than 100.

The largest known basic number, 60, is found in the Babylonian sexagesimal system. It is difficult to explain the reasons for such a large unit group. It has been suggested by several authors that it is the result of a merger of two different number systems. We still use this system when measuring time and angles in minutes and seconds. Other basic numbers than those mentioned here are quite rare. We may detect a trace of a 12 or duodecimal system in our counts in dozens and gross. Certain African tribes use basic groups of 3 and 4. The binary or dyadic system, in which 2 or a pair is the basic concept, has been used in a rudimentary form by Australian indigenes. The dyadic system is, however, a system whose simple properties often have a special mathematical usefulness.

1–3. The number systems.

When the basic counting group is fixed, the numbers exceeding the first group would be obtained by counting afresh in a new group, then another, and so on. For instance, in a quinary system where the basic five group might be called one h(and), one would count one h. and one, one h. and two, 2h. (10), 3h. and 2 (17), and so on. After one had reached five hands (25), one might say hand of hands (h.h.) and begin over again. So as an example, one would denote 66 by 2hh and 3h and 1, that is, 2 × 25 + 3 × 5 + 1. Clearly this process can be extended indefinitely by introducing higher groups

hhh = 125 = 5³ hhhh = 625 = 5⁴

In this manner one arrives at a representation of any number as an expression

(1–1)

where each coefficient a_i is one of the numbers 0, 1, 2, 3, 4.

To be quite correct, one should observe that this particular example historically is fictitious, since no people is known to have developed and used a completely general system (1–1) with the base 5. But this systematic procedure for the construction of a number system was certainly the guiding principle in the evolution of our decadic number system and of many other systems. To confirm this assertion further one can turn to the philological analysis of our number terms. Through the laws of comparative linguistics one can trace a word like eleven to one left over, and similarly twelve to two over. There is some indication that our fundamental word ten may be derived from an Indo-European root meaning two hands. The word hundred comes from an original term ten times (ten). It is further interesting to note that the names for thousand are unrelated in the various main branches of the Indo-European languages; hence it is probably a rather late construction. The word itself seems to be derived from a Proto-Germanic term signifying great hundred.

In our decadic system all numbers are put in a form analogous to (1–1)

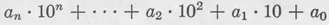
(1–2)

where the coefficients take values from 0 to 9. In general, in the subsequent chapters, we shall understand by a number system with the base b a system in which we represent the numbers in the form

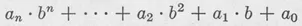
(1–3)

where the coefficients a_i are numbers from 0 to b–1.

It should be mentioned that relatively few peoples developed their number systems to this perfection. Also, in many languages one finds other methods for the construction of numbers. As an example of irregular construction let us mention that in Welsh the number words from 15 to 19 indicate 15, 15 + 1, 15 + 2, 2 × 9, 15 + 4. Subtraction occurs often as a method; for instance, in Latin, un-de-viginti = 20–1 = 19, duo-de-sexaginta = 60–2 = 58. Similar forms exist in Greek, Hindu, Mayan, and other languages.

The Mayan number system was developed to unusually high levels, but the system has one peculiar irregularity. The basic group is 20, but the group of second order is not 20 × 20 = 400 as one should expect, but 20 × 18 = 360. This appears to be connected with the division of the Mayan year into 18 months each consisting of 20 days, supplemented with 5 extra days. The higher groups in the system are

360 × 20, 360 × 20², ...

1–4. Large numbers.

As one looks at the development of number systems in retrospect it seems fairly simple to construct arbitrarily large numbers. However, in most systems the span of numbers actually used is very limited. Everyday life does not require very large numbers, and in many languages the number names do not go beyond thousands or even hundreds. We mentioned above that the term one thousand seems to have made a relatively late appearance in the Indo-European languages. The Greeks usually stopped at a myriad or ten thousand. For a long period the Romans did not have names or symbols for groups above 100,000. There exists in Rome an inscription on the Columna Rostrata commemorating the victory over Carthage at Mylae in the year 260 B.C. in which 31 symbols for 100,000 were repeated to signify 3,100,000. The Hindus had a peculiar attraction to large numbers, and immense figures occur commonly in their mythological tales and also in many of their algebraic problems. As a consequence, there existed particular names for the higher decadic groups to very great powers of 10. For instance, in a myth from the life of Buddha one finds the denominations up to 10¹⁵³.

Even our own number system has not been developed systematically to this extent. The word for one million is a fairly recent construction, which seems to have originated in Italy around A.D. 1400. The concept one bill...