![]()
1
Chance Encounters
Our brains are just not wired to do probability problems very well. PERSI DIACONIS 1989 |
Everyone has been touched in some way by the laws of chance. From shuffling cards for a game of bridge, to tossing a coin at the start of a football game, to awaiting the outcome of the Selective Service draft lottery, to weighing the risks and benefits of knee surgery, most of humanity encounters chance daily. The statistics that describe our probabilistic world are everywhere we turn: One-third don’t survive their first heart attack. The chance of a DNA match is 1 in 100 billion. Four out of every 10 marriages in America end in divorce. Batting averages, political polls, and weather predictions are pervasive, but an understanding of the concepts underlying these statistics and probabilities is not.
Misconceptions abound, and certain concepts seem to be particularly problematic. To even the mathematically enlightened, some issues in probability are not so intuitive. Despite curriculum reforms that have emphasized the teaching of probability in the schools, most experienced teachers would probably agree with the math teacher who commented, “Teaching statistics and probability well is not easy.”1
Even in very serious decision-making situations, such as assessing the evidence of guilt or innocence during a trial, most people fail to properly evaluate objective probabilities. The psychologists Daniel Kahneman and Amos Tversky illustrated this with the following example from their research:
A cab was involved in a hit and run accident at night. Two cab companies, the Green and the Blue, operate in the city. You are given the following data:
(a) 85% of the cabs in the city are Green and 15% are Blue.
(b) A witness identified the cab as Blue. The court tested the reliability of the witness under the same circumstances that existed on the night of the accident and concluded that the witness correctly identified each one of the two colors 80% of the time and failed 20% of the time.
What is the probability that the cab involved in the accident was Blue rather than Green?2
A typical answer is around 80 percent. The correct answer is around 41 percent. In fact, the hit-and-run cab is more likely to be Green than Blue.
Kahneman and Tversky suspect that people err in the hit-and-run problem because they see the base rate of cabs in the city as incidental rather than as a contributing or causal factor. As other experts have pointed out, people tend to ignore, or at least fail to grasp, the importance of base-rate information because it “is remote, pallid, and abstract,” while target information is “vivid, pressing, and concrete.”3 In evaluating the eyewitness’s account, “jurors” seem to overrate the eyewitness’s likelihood of accurately reporting this specific hit-and-run event, while underrating the more general base rate of cabs in the city, because the latter information seems too nonspecific.
Base-rate misconceptions are not limited to the average person without an advanced mathematics education. Sophisticated subjects have the same biases and make the same mistakes—when they think intuitively. In a study at a prominent medical school, physicians, residents, and fourth-year medical students were asked the following question:
If a test to detect a disease whose prevalence is one in a thousand has a false positive rate of 5 percent, what is the chance that a person found to have a positive result actually has the disease, assuming you know nothing about the person’s symptoms or signs?4
Almost half of the respondents answered 95 percent. Only 18 percent of the group got the correct answer: about 2 percent. Those answering incorrectly were once again failing to take into account the importance of the base-rate information, namely, (only) 1 person among 1000 tested will have the disease.
The commonsense way to think mathematically about the problem is this: Only 1 person in 1000 has this disease, as compared with about 50 in 1000 who will get a false positive result (5 percent of 999). It is far more likely that any one person who tests positive will be one of the 50 false positives than the 1 true positive. In fact, the odds are 1 in 51 that any one person who tests positive actually has the disease, and that translates into only a 2 percent chance, even in light of the positive test.
Another way to state the issue is that the chances of having this disease go from 1 in 1000 when one takes the test to 1 in 51 if a person gets a positive test result. That’s a big jump in risk, to be sure, but it’s a far cry from the 95 out of 100 chance many people erroneously believe they have after a positive test.
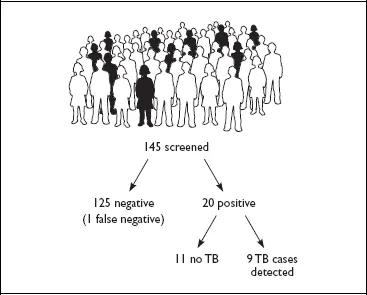
False positives are not human errors or lab errors. They happen because screening tests are designed to be overly sensitive in picking up people who deviate from some physiological norm, even though those people do not have the disease in question. In order to be sensitive enough to pick up most people who have tuberculosis, for example, skin tests for TB infection will always yield a positive result for around 8 percent of people who do not have the infection but who have other causes for reaction to the test; if 145 people are screened, roughly 20 will test positive. Yet only 9 of these 20 will turn out to have TB infection.5
The rate of false positives can be reduced by making screening tests less sensitive, but often this just increases the percentage of false negatives. A false negative is a test result that indicates no disease in a person who actually has the disease. Because false negatives are usually considered more undesirable than false positives (since people who get a false negative will not receive prompt treatment), the designers of screening tests settle on a compromise—opting for a very small percentage of false negatives and a somewhat larger percentage of false positives than we might prefer. In the case of tuberculosis, whereas roughly 7.5 percent of people tested will receive a false positive result, only 0.69 percent (roughly 1 person out of every 145 screened) will get a false negative test result. In other words, out of 145 people screened for TB using this method, 9 cases of the disease will be detected and 1 case will remain undetected (see Figure 1).
FIGURE 1 Really well, or really sick? If a person has a routine screening test for tuberculosis, she or he has a 10 in 145 (about 7 percent) chance of having the infection at the time of the test. If the result comes back positive, the patient’s odds of having TB go up to 9 in 20 (45 percent). If the result comes back negative, the patient still has a 1 in 125 chance of having the disease (about 0.8 percent); the original risk has been drastically reduced, but not eliminated, by the doctor’s “good news.”
Considering that even highly educated medical personnel can make errors in understanding probabilistic data of this kind, we should not be at all surprised that probability often seems to be at odds with the intuitive judgments of their patients and other ordinary people.
In addition to base-rate misconceptions, psychologists have shown that people are subject to other routine fallacies in evaluating probabilities, such as exaggerating the variability of chance and overattending to the short run versus the long run.6 For example, the commonly held notion that, on a coin toss, a tail should follow a string of heads is erroneous. Children seem particularly susceptible to this fallacy. Jean Piaget and Barbel Inhelder, who studied the development of mathematical thinking in children and whose work will be described frequently in the following chapters, pointed out that “by contrast with [logical and arithmetical] operations, chance is gradually discovered.”7
One would think that the experiences acquired over a lifetime ought to solidify some correct intuitions about statistics and probability. Intuitive ideas about chance do seem to precede formal ideas, and, if correct, are an aid to learning; but if incorrect, they can hinder the grasp of probabilistic concepts. Kahneman and Tversky have concluded that statistical principles are not learned from everyday experience because individuals do not attend to the detail necessary to gain such knowledge.8
Not surprisingly, over the course of our species’ history, acquiring an understanding of chance has been extremely gradual, paralleling the way an understanding of randomness and probability develops in an individual (if it does). Our human dealings with chance began in antiquity, as we will see in Chapters 2 and 3. Archaeologists have found dice, or dice-like bones, among the artifacts of many early civilizations. The practice of drawing lots is described in the writings of ancient religions, and priests and oracles foretold the future by “casting the bones” or noting whether an even or odd number of pebbles, nuts, or seeds was poured out during a ceremony. Chance mechanisms, or randomizers, used for divination (seeking divine direction), decision making, and games have been discovered throughout Mesopotamia, the Indus valley, Egypt, Greece, and the Roman Empire. Yet the beginnings of an understanding of probability did not appear until the mid-1500s, and the subject was...