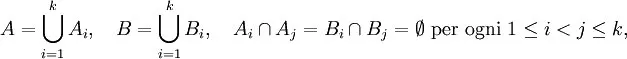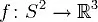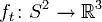Introduzione fisico-matematica

Rosanna Festa

• Editore: Youcanprint
• Anno: 2021
• eBook ISBN: 9791220316460
• Argomento: Filosofia
• Categoria: Filosofia ed etica nella scienza

Il pragmatismo è un movimento filosofico largamente diffuso negli Stati Uniti tra la fine del XIX secolo e l'inizio del XX. Il termine "pragmatismo" mette in rilievo la tesi fondamentale secondo cui il significato di qualsiasi cosa è determinato dalla sua rilevanza pratica. Originariamente nella definizione di Peirce, considerato il fondatore del movimento, il pragmatismo è un metodo per ottenere chiarezza linguistica e concettuale quando gli uomini affrontano problemi intellettuali.
Il formalismo è da considerarsi un tipo di riduzionismo matematico per il principio che una consistente assiomatizzazione di tutta la matematica è impossibile perché non è possibile non derivare dal sistema alcuna contraddizione. Il linguaggio quindi è fondamentale. Basti pensare che nei primi anni del nostro secolo le fondamenta della matematica sono state vigorosamente scosse dalla scoperta di contraddizioni, dei paradossi o antinomie, soprattutto nella teoria degli insiemi.
Il fare matematica è una creazione di significato. La ricerca dei fondamenti della matematica è utile nella filosofia della matematica, perché può fornire importanti risultati nella fisica, in particolare nella meccanica quantistica per rispondere alla domanda postasi da Einstein nel 1935: ”può la descrizione quanto-meccanica della realtà fisica essere considerata completa?” e nella logica, per rispondere ai problemi sulla natura degli assiomi matematici.

Capitolo primo

La matematica sperimentale

Russell afferma che “tutta la matematica pura tratta esclusivamente di concetti definibili in termini di un numero piccolissimo di concetti logici fondamentali”, il problema della ricerca dei fondamenti nella matematica non è recente: nell’800 la scuola di Weierstrass arrivò all’“aritmetizzazione dell’analisi“, cioè la riduzione dei concetti fondamentali dell’analisi (la matematica che ha come cardine la teoria dei “numeri reali”) ai concetti dell’aritmetica (la matematica che ha come cardine la teoria dei numeri interi positivi, cioè dei numeri naturali, e per estensione, dei numeri razionali). Galileo sosteneva che le proposizioni aritmetiche sono vere anche in fisica, mentre Leonardo da Vinci sosteneva che “nessuna umana investigazione può chiamarsi vera scienza, se non passa per le matematiche dimostrazioni”. Sia Galileo sia Newton intentarono di raggiungere la comprensione delle leggi generali, di tipo matematico, che descrivono il funzionamento dell’universo. Newton sosteneva che in ambito filosofico dobbiamo cercare la dimensione vera e matematica di spazio e tempo assoluti. Galileo rilevò l’importanza della matematica sperimentale o matematica strumentale. Poiché la matematica decresce dalla fisica alla chimica alla biologia per il motivo che si passa dal fisico al descrittivo, sembra che esista una relazione che va dal fisico al biologico verso la natura umana. La chimica infatti è l’anello mancante tra fisica e biologia, come per la chimica organica, che si occupa delle caratteristiche chimiche e fisiche delle molecole organiche. La biochimica che è lo studio della chimica della vita, è a sua volta “un ponte fra la biologia e la chimica che studia le reazioni chimiche complesse che danno origine alla vita: oggetto di studio sono la struttura e le trasformazioni dei componenti delle cellule, come proteine, carboidrati, lipidi, acidi nucleici e altre biomolecole.,e la geochimica organica, che è una branca della geochimica che si occupa dello studio degli impatti e dei processi riguardanti gli organismi viventi o precedentemente morti, concentrandosi in particolare sulla caratterizzazione della materia organica presente sulla Terra”. La matematica sperimentale è utile nella descrizione naturale che ci permette di costruire degli assiomi o dei sistemi di riferimento. Il problema dei fondamenti nella scienza è ridotto nel caso si giudichi da quale disciplina derivino tutte le altre, invece è complesso quando si riconosce che tutte le scienze possiedono sia parametri qualitativi sia parametri quantitativi. Il problema dei fondamenti della matematica (ovvero quale branca della matematica è quella dalla quale derivano tutte le altre) è un problema riduzionista. Se gli assiomi sono leggi naturali e universali che noi prendiamo come riferimento settoriale come dimostrazione, siamo in grado di dire che la matematica contiene un “principio dimostrativo”¹ che non appartiene a nessun’altra disciplina. Esistono, infatti, teorie in filosofia che attingono direttamente dalla matematica. Il determinismo ha una natura matematica ovvero individua un sistema di relazioni² e di cause compatibili con la matematica che arriva al calcolo infinitesimale³ nel 18° secolo. I “sillogismi matematici” hanno la funzione di rilevare nuove strutture logiche reali, in altre parole nuovi sistemi logici, esempi di sillogismi matematici sono i ragionamenti delle geometrie non euclidee e del logicismo. I sillogismi matematici costituiscono l’apertura logica verso i sistemi complessi.

Implicazioni filosofiche

Si suppone che alcune scienze come la sociologia e la psicologia, che appartengono tipicamente alle scienze moderne, e scienze che hanno più forti legami relazionali con la matematica, come biologia, medicina, chimica, e fisica abbiano subito profonde rivoluzioni storiche, e siano molto indietro nello sviluppo di teorie logiche di tipo matematico-implicazioni.

Il correlativismo sostiene che esiste solo una realtà: quella matematica, cioè sostiene che la matematica è la base o i fondamenti delle altre scienze. Questa proposizione è nettamente filosofica, ma si può affermare solo dal punto di vista metodologico. Essa afferma che

-la matematica è un parametro universale di misura dei fenomeni

-ciò che non si può esprimere matematicamente esprime un certo livello d’indeterminazione

-ciò che si esprime attraverso un processo matematico può chiamarsi processo logico-matematico

Platone può essere considerato correlativista. Berti afferma che “non bisogna dimenticare che al tempo di Platone la matematica era l’unica scienza che fosse pervenuta a darsi uno statuto epistemologico compiuto, cioè l’unica scienza che avesse raggiunto propriamente il livello di scienza, cosa che non si poteva dire per la fisica, per la biologia ecc. Questo fa sì che la matematica assuma un grande valore agli occhi di Platone; ”la matematica appunto, è scienza, non è conoscenza empirica”, ma conoscenza razionale.

Logiche invarianti

La matematica euristica occorre in tutti i casi in cui è necessario un puro calcolo che prescinde dai significati associabili ai suoi simboli e alle sue espressioni, in altre parole dall’esperienza sensibile. Si ha la dimostrazione che molte realtà concettuali siano erronee se non facendo ricorso alla logica matematica e mostra che la sintesi matematica del fenomeno fisico è un po’ come la dimostrazione della natura del fenomeno, sia esso dinamico o statico. Rappresenta gli inganni in cui cade la mente staticamente empirica, e che porta a pensare a questa matematica come una matematica “concettuale”, aprendo il problema degli universali. Porfirio in un passo alle Categorie di Aristotele (Isagoge del 270 d.C. circa, ma nota nella traduzione latina fatta da Boezio attorno al 500): nota “sui generi e le specie non dirò se essi sussistano oppure siano posti soltanto nell’intelletto, né nel caso che sussistano, se siano corporei o incorporei, se separati dalle cose sensibili o situati nelle cose stesse ed esprimenti i loro caratteri comuni”. Che gli universali sussistono in modo incorporeo extramentale e separato dalle cose può essere affermazione platonica o di un realismo radicale. Che, invece, essi siano solo nelle cose come caratteri comuni e debbano pertanto essere posti alla base delle nostre conoscenze, è più un’affermazione aristotelica o del realismo moderato. Il realismo moderato è una teoria più organizzata perché ammette che pur essendo la mente qualcosa di complesso essa riconosce la complessità matematica degli enti naturali, rappresentando questi due sistemi strutturati di diversa complessità fisica. Rientrano nella matematica formale il paradosso di Banach-Tarski, il paradosso della linea scomparsa e il paradosso di Smale (1).

• Stabilito per la prima volta da Stefan Banach e Alfred Tarski nel 1924, il paradosso di Banach-Tarski o paradosso di Hausdorff-Banach-Tarski è il famoso paradosso del "raddoppiamento della sfera" ("doubling the ball"), che stabilisce che, adoperando l'assioma della scelta, è possibile prendere una palla nello spazio a 3 dimensioni, suddividerla in un insieme finito di pezzi (non misurabili) e, utilizzando solo rotazioni e traslazioni, riassemblare i pezzi in modo da ottenere due palle dello stesso raggio dell'originale.

Banach e Tarski intendevano, con questa dimostrazione, confutare l'assioma della scelta, ma la natura della dimostrazione ha portato altri matematici ad assumere che l'assioma della scelta produca semplicemente dei risultati contro intuitivi.

Il paradosso afferma in sostanza che non esiste una generica misura invariante per traslazione in uno spazio tridimensionale che sia sempre in grado di associare a uno spazio la misura del suo volume. Difatti la "creazione" della seconda palla è ottenuta tramite l'assemblaggio dei volumi non individuati dalla misura. La dimostrazione che non esista una generica misura invariante per traslazione in uno spazio tridimensionale era già stata ottenuta tramite l'insieme di Vitali, ma il paradosso di Banach-Tarski mette in evidenza le paradossali conseguenze di questo fatto.

Impostazione formale

Supponiamo che G sia un gruppo che agisce su un insieme X. Nel caso speciale più importante, X è uno spazio Euclideo n-dimensionale, e G consiste in tutte le isometrie di X, cioè le trasformazioni biunivoche di X in se stesso che preservano le distanze. Due figure geometriche che possono essere trasformate l'una nell'altra vengono chiamate congruenti, questa terminologia sarà estesa alla G-azione generale. Due sottoinsiemi A e B di X sono chiamati G -equiscomponibili, o equiscomponibili rispetto a G, se A e B possono essere partizionati nello stesso numero finito di pezzi G-congruenti. È facile vedere che ciò definisce una relazione di equivalenza tra tutti i sottoinsiemi di X. ~ Formalmente, se

e ci sono elementi g₁,...,g_k di G tali che per ogni i tra 1 e k, g_i (A_i ) = B_i , allora diremo che A e B sono G-equiscomponibili usando k pezzi. Un insieme E viene chiamato paradossale se ha due sottoinsiemi disgiunti A e B tali che A ~ E e B ~ E.

Usando questa terminologia il paradosso di Banach–Tarski può essere riformulato come segue:

Una palla a tre dimensioni Euclidee è equiscomponibile a due copie di se stessa.

Il paradosso della linea scomparsa

Il paradosso della linea scomparsa è un paradosso geometrico per cui una linea sembra scomparire nel nulla.

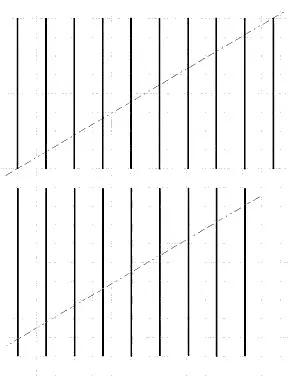
Si consideri l'immagine seguente:

Nella parte superiore sono tracciate dieci linee verticali. Si tagli il foglio secondo la linea tratteggiata e si ricomponga come nella figura inferiore. Ora le linee sono diventate nove.

Soluzione

Il paradosso è facilmente superabile costatando che la lunghezza della linea scomparsa si è suddivisa equamente tra le altre linee che sono ora più lunghe.

Varianti

Esistono molte varianti di questo paradosso, a volte rese più spettacolari grazie a rappresentazioni di oggetti che scompaiono. Un simile trucco, applicato al contrario, è utilizzato per falsificare le banconote. Da dieci banconote è possibile ottenerne undici leggermente più corte. La ripetizione del numero di serie su due angoli estremi delle banconote ha la funzione di prevenire questo trucco. Occorre sempre verificare che i due numeri corrispondano, in particolare se la banconota è stata riparata con nastro adesivo.

Il paradosso di Smale

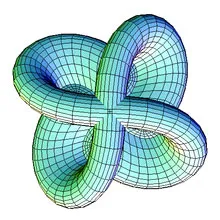
Superficie di Morin vista "dall'alto"

Il paradosso di Smale, in topologia differenziale, afferma che è possibile in uno spazio tridimensionale rivoltare una sfera, ovvero con la parte interna e esterna invertite, senza creare fori o pieghe, ma al più auto-intersezioni. Più precisamente sia

un'immersione canonica; allora esiste un'omotopia di immersione

tale che f₀ = f e f₁ = − f.

Questi aspetti matematici, da configurazioni a più stati, dimostrano che gli oggetti sensibili si presentano già preliminarmente in configurazioni tipiche o forme, le quali derivano dall’esperienza e che la realtà in cui viviamo è precostituita dalle configurazioni in cui si danno gli oggetti quotidiani. Probabilmente, di fronte a dei paradossi simili H. Putnam a corto di nozioni matematiche sarebbe caduto nella contraddizione da lui stesso chiamata teoria del riferimento, cioè sull’ipotesi che “i significati non sono nella testa” e che le nostre credenze sul mondo esterno potrebbero essere una semplice illusione, sarebbe cioè caduto nel dubbio iperbolico che noi potremmo essere cervelli in una vasca privi di reali contatti con il mondo esterno. Esiste quindi un’omotopia ma anche un omotipia, nel senso che esistono due possibili soluzioni del problema.

La ricerca applicata

Il campo delle reazioni chimiche non spontanee, come la chimica nucleare, non si può chiamare un campo della ricerca tradizionale pura. Così i campi della chimica maggiormente legati al dibattito scientifico, come la chimica inorganica, la biochimica o la chimica dell’ambiente, possono assumere il ruolo di teorie ausiliarie. La chimica moderna ha superato oggi gli obiettivi tradizionali dello studio degli atomi, e quindi degli elettroni e le proprietà degli elementi, dei fluidi e delle reazioni chimiche spontanee. In questi casi l’equazione scientifica da adottare è un processo da definire perché la scienza è qualcosa che influenza a sua volta la matematica, quindi non è la prima volta che le argomentazioni naturalistiche vadano a fallimento. Non si può cioè dire che la natura sia un positivo e compiuto orizzonte di riferimento, si pensi all’energia rinnovabile in biochimica e la sostituzione degli organi in biomedica. Siamo arrivati a un punto in cui si rafforza la distinzione tra ricerca scientifica pura e ricerca applicata, nella prima la libertà andrebbe sempre e comunque riproposta e garantita, e la ricerca applicata andrebbe tuttavia definita come un programma di esperimenti con una base empirica. Infatti, la ricerca nucleare e la bioetica segnano un netto contrasto con le scienze tradizionali della ricerca pura. In ogni caso la bioetica di oggi è legittimata da valori etici accomunanti della dignità umana. Tuttavia non siamo riusciti a salvare la ricerca dall’osservatorio “sperimentale” delle prime bombe nucleari, come quelle scoppiate a Hiroshima e Nagasaki, e gli studi d’ingegneria genetica nei campi di concentramento, durante la seconda guerra mondiale. La non completa unificazione delle scienze è anche limitata da una questione linguistica, cioè dal fatto di limitare al massimo l’incommensurabilità, cioè quando tutte le conseguenze della prima teoria sono diverse e non contradditorie con tutte le conseguenze della seconda teoria. Sono cioè incommensurabili teo...

Indice dei contenuti

• Cover
• Indice
• Frontespizio
• Copyright
• Capitolo primo
• Capitolo secondo
• Capitolo terzo
• Capitolo quarto