Cartesio - La matematica incontra la geometria

Enrico Rogora, AA.VV., AA.VV., Enrico Rogora

• Editore: Pelago
• Anno: 2021
• eBook ISBN: 9791280714923
• Argomento: Storia
• Categoria: Didattica generale

Considerato uno dei più grandi filosofi moderni, Cartesio pubblicò un solo testo matematico. Ma in un centinaio di pagine rivoluzionò la disciplina. La sua Geometria si propone di sviluppare un metodo universale su cui fondare in modo rigoroso l'indagine filosofica e scientifica. Contiene però anche molti risultati tecnici importanti e molte nuove idee. Cartesio mostra come l'aritmetica, l'algebra e la geometria possano essere combinate per risolvere ogni problema, attraverso tecniche innovative per collegare la costruzione di una curva alla sua equazione algebrica, classificare le curve in relazione alle loro equazioni algebriche e usare esclusivamente la geometria per risolvere i problemi algebrici: la sua algebra dei segmenti mette al servizio della geometria la potenza di astrazione e di semplificazione dell'algebra senza bisogno dei numeri. Il passo successivo, non del tutto svolto da Cartesio, ma reso possibile dal suo lavoro, porterà all'invenzione della geometria analitica, ovvero all'identificazione di ogni elemento geometrico con un insieme di numeri che ne esprimono le coordinate su un piano, che non a caso chiamiamo cartesiano.

FOCUS

L’IMPORTANZA DI CARTESIO

L’ALGEBRA DEI SEGMENTI

Cartesio pubblicò un solo scritto matematico, la Geometria (Géométrie). Il suo contenuto si può condensare come un metodo per ben realizzare le costruzioni geometriche. Non a caso la Geometria è una delle tre appendici, insieme alla Diottrica e a Le Meteore, del Discorso sul metodo per ben condurre la propria ragione e ricercare la verità nelle scienze e la scienza di cui si occupa è quella delle costruzioni geometriche, non solo quelle che si possono fare con riga e compasso, ma tutte quelle che si possono fare con l’ausilio di curve geometriche ben più generali, cioè le curve che si possono descrivere con un’equazione algebrica.

È evidente da questa premessa che il pensiero filosofico e quello matematico di Cartesio sono profondamente legati e che il carattere principale della Geometria è metodologico. Scrive infatti egli stesso a uno dei suoi numerosi corrispondenti:

“NELLA GÉOMÉTRIE PROVO A DARE UN METODO GENERALE PER RISOLVERE TUTTI I PROBLEMI CHE NON SONO MAI STATI RISOLTI.”

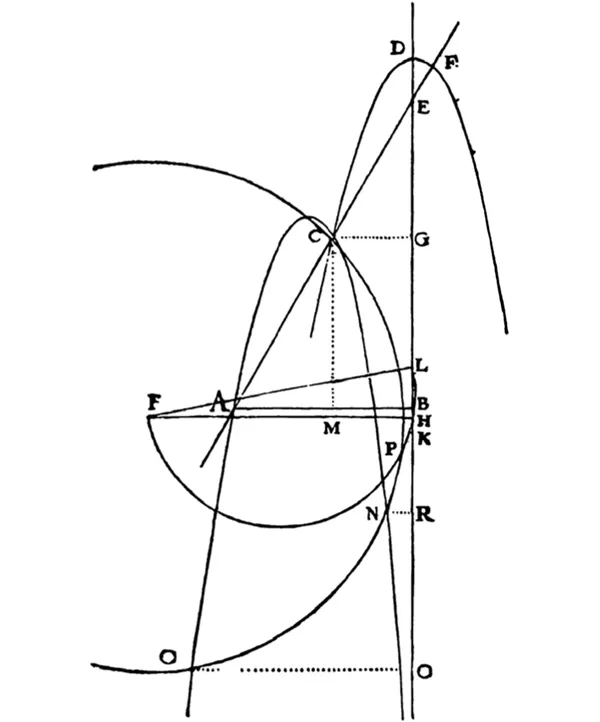
Figura tratta dalla Geometria e relativa al metodo per trovare le soluzioni di equazioni di sesto grado.

Oltre all’importanza sul piano metodologico, la Geometria contiene molti risultati tecnici importanti e molte nuove idee. Indicare la scoperta matematica più importante di Cartesio è un compito particolarmente difficile perché dipende fortemente dalla prospettiva da cui si guarda alla sua opera: metodologica, tecnica o della novità delle idee. Da quest’ultimo punto di vista, quella che mi sembra più ricca di conseguenze per la matematica è questa:

L’idea che sia possibile costruire un’algebra dei segmenti che mette al servizio della geometria la potenza di astrazione e di semplificazione dell’algebra senza bisogno dei numeri, che all’epoca di Cartesio non erano ancora ben definiti in tutta la loro generalità.

Oggi siamo così abituati a pensare alla geometria in termini numerici, cioè a identificare un punto della retta con un numero reale, da dimenticare che al tempo di Cartesio i numeri reali non esistevano e i numeri negativi erano ancora considerati con sospetto e da sottovalutare quindi la scoperta dell’algebra dei segmenti.

Cartesio comincia la Geometria mostrando come sia possibile costruire con riga e compasso, a partire da due segmenti qualsiasi, la somma, la differenza, il prodotto, la divisione e la radice quadrata.

Il segmento somma di due segmenti e il segmento differenza di un segmento più grande con uno più piccolo non sono una novità, ma è Cartesio, per la prima volta nella storia della matematica, a pensare al prodotto e alla divisione come segmenti. Nella matematica greca ed ellenistica, e ancora fino ai tempi di Cartesio, il prodotto di due segmenti era un rettangolo e la divisione un rapporto tra due grandezze omogenee, cioè, come spiegato da Euclide nel libro quinto degli Elementi, una classe di equivalenza, che non si prestava ad essere manipolata agevolmente in maniera algebrica. Pensare al prodotto come un rettangolo, pur offrendo un’interpretazione intuitiva e suggestiva, limita fortemente la generalità dell’operazione. Infatti, se il prodotto di due segmenti è un rettangolo, il prodotto di tre è un parallelepipedo, ma il prodotto di quattro non ha più senso. Per questa ragione l’algebra geometrica dei greci nasce zoppa e non può diventare uno strumento efficace per la geometria.

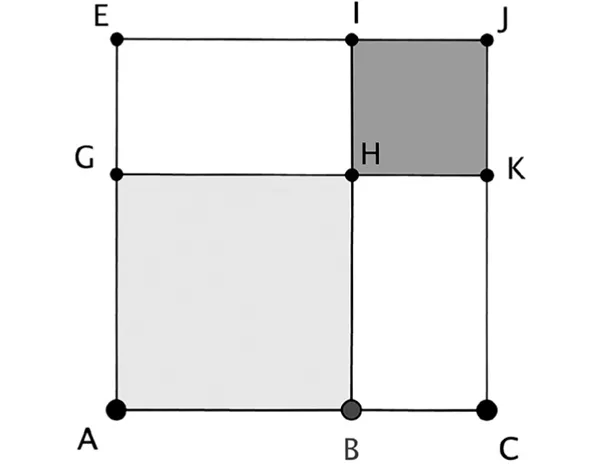
L’algebra dei greci interpreta geometricamente le proprietà del prodotto in maniera molto intuitiva; per esempio l’identità (a + b) × (a+ b) = a × a + 2 a × b + b × b si “vede” nella figura dove AB = a e BC = b, ma questa algebra non è abbastanza generale.

Per definire il prodotto Cartesio fa riferimento alla figura qui sotto, che abbiamo riprodotto dalla prima edizione della Geometria del 1637.

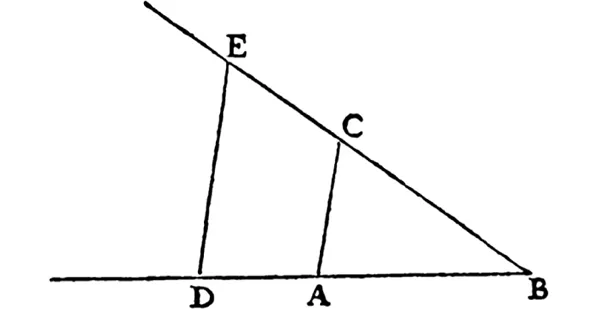
Per moltiplicare BC per BD bisogna innanzitutto riportare sulla semiretta BD il segmento unità BA. A questo punto basta, scriveva Cartesio, «unire i punti A e C, poi tracciare DE parallela a CA, e BE è il prodotto di questa moltiplicazione. Oppure, se occorre dividere BE per BD, congiunti i punti E e D, traccio AC parallela a DE, e BC è il prodotto di questa divisione».

Questa semplice idea, che utilizza in maniera cruciale il segmento unità, permette di definire il prodotto e la divisione di segmenti come un nuovo segmento e definisce, insieme alla somma e alla differenza, un’algebra molto più potente dell’algebra geometrica dei greci, che diventa, nelle mani del suo creatore, uno strumento rivoluzionario per affrontare con metodo le costruzioni geometriche.

Cartesio si lamentava del fatto che le costruzioni dei greci fossero prive di metodo e che ogni volta bisognasse cercare «la strada» basandosi sull’intuizione geometrica, senza una guida sistematica. Egli pensava che l’algebra di segmenti potesse essere una tale guida. Quanto avesse ragione è dimostrato dal fatto che la geometria analitica, figlia dell’algebra dei segmenti, è per tutti più facile della geometria di Euclide.

L’algebra non era considerata, ai tempi di Cartesio, una disciplina rigorosa. Si cercava sistematicamente la dimostrazione dei risultati ottenuti con i suoi metodi per via geometrica. L’interpretazione geometrica delle operazioni data da Cartesio e la dimostrazione geometrica delle loro proprietà mostra una volta per tutte che le manipolazioni formali che fanno uso delle proprietà delle quattro operazioni forniscono risultati perfettamente rigorosi.

Ci possiamo chiedere perché questo modo così semplice di interpretare prodotto e divisione non si sia imposto prima. Io credo che la difficoltà stia nella necessità di fissare un elemento ad arbitrio nella definizione cartesiana del prodotto e del quoziente. Infatti bisogna fissare a priori il segmento unità. Cambiando il segmento unità, cambia il risultato del prodotto. Questo elemento arbitrario è una pulce fastidiosa nell’orecchio di un geometra precartesiano perché è un elemento posticcio, estraneo all’universo euclideo.

Un piccolo passo, come quello di aggiungere l’unità agli elementi fondamentali della geometria, può portare a una rivoluzione concettuale e la difficoltà di compiere questo piccolo passo è spesso legata a pregiudizi culturali la cui importanza è difficile da valutare propriamente quando questi passi vengono fatti. Si pensi al pregiudizio di voler spiegare i moti dei pianeti con le circonferenze o a quello di considerare gli assiomi della geometria euclidea come proprietà oggettive dello spazio fisico.

Nonostante queste premesse indichino chiaramente l’importanza degli intrecci tra filosofia e matematica nell’opera di Cartesio, lasceremo poco spazio all’approfondimento di questi intrecci per coerenza con la prospettiva di divulgazione matematica con cui vogliamo guardare alla sua opera.

La scelta di cominciare con l’algebra dei segmenti offre anche l’occasione di sgombrare immediatamente il campo dall’idea che Cartesio abbia inventato la geometria analitica come la intendiamo oggi, ovvero l’identificazione dei punti del piano con le coppie di numeri reali e di aver sostituito le figure geometriche con equazioni e disequazioni. Naturalmente ci sono nell’opera di Cartesio molti fili che si intrecciano con questi sviluppi, ma non è a questo che mira Cartesio.

La sua algebra dei segmenti viene anzi sviluppata proprio per poter utilizzare l’algebra nella geometria senza usare i numeri e nella sua opera non viene mai introdotta o presentata una curva mediante la sua equazione.

LE OPERE SCIENTIFICHE

La Geometria è uno dei testi fondamentali della matematica moderna. Introduce molte novità rispetto alla tradizione matematica greca ed ellenistica, che si protrasse fino a Galileo e alla sua scuola, e prepara la strada ai nuovi e impetuosi sviluppi della matematica del XVII secolo. Fu pubblicata nel 1637 come appendice al Discorso sul metodo. Insieme alle altre due appendici, la Diottrica e Le Meteore, illustra l’applicazione dei principi generali del metodo cartesiano alla risoluzione di problemi concreti delle scienze naturali. A differenza delle altre appendici e del Metodo stesso, la Geometria non è pensata da Cartesio come lettura per tutti ma presuppone una buona conoscenza della matematica da parte del lettore.

Il giudizio di Cartesio sull’importanza della Geometria è espresso magistralmente, con toni tra l’arrogante e lo spaccone, in una le...

Indice dei contenuti

• Collana
• Frontespizio
• Copyright
• Indice
• La matematica universale
• PANORAMA
• FOCUS a cura di Enrico Rogora
• APPROFONDIMENTI
• Piano dell'opera