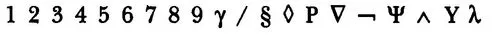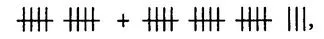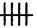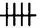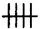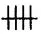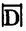Zero. Storia di una cifra

Robert Kaplan

• Editore: BUR
• Anno: 2012
• Print ISBN: 9788817125369
• eBook ISBN: 9788858630655
• Argomento: Matematica
• Categoria: Matematica generale

Senza lo zero, la matematica come la conosciamo non esisterebbe. Ma qual è l'origine di questo simbolo che rappresenta il nulla? Quando fu usato la prima volta? E quali conseguenze ha portato nel nostro modo di contare e pensare? Robert Kaplan, in un viaggio sorprendente nell'evoluzione della matematica, ci racconta tutto della sua storia. Ignoto ai greci e ai romani, lo zero giunse in Occidente nel Medioevo attraverso gli arabi, che a loro volta ne avevano appreso la nozione dagli indiani. Poi, con i grandi rivoluzionari della matematica moderna, assunse nuovi significati, fino a conquistare un ruolo centrale nella nostra stessa visione dell'universo. Al punto che, come ci ricorda Kaplan, "guardate attraverso lo zero e vedrete il mondo. Esso consente di mettere a fuoco il maestoso, organico sviluppo della matematica, e questa, a sua volta, la natura complessa della realtà".

Dedica

A Frank Brimsek

3 ore 51 minuti 54 secondi

RINGRAZIAMENTI

In primo luogo e soprattutto, ai fari che orientano la mia vita: Ellen, il cui spirito informa questo libro; e Barry Mazur, la cui energia e il cui intuito non hanno limiti. Inoltre, il libro sarebbe niente, invece che sul niente, se non fosse per Christopher Doyle, Eric Simonoff e Dick Teresi. Moltissimo ha anche guadagnato dall’ispirazione editoriale di Peter Ginna e Stefan McGrath.

Nella comunità degli studiosi, sono molti coloro che devo ringraziare per il tempo e le conoscenze generosamente messi a disposizione. Jon Tannenhauser ha prodigato esperienza e suggerimenti, come Mira Bernstein. Peter Renz, la cui riserva d’informazioni è più ricca perfino della sua biblioteca, è stato inestimabile. Sono molto grato dell’aiuto anche a Gary Adelman, a Johannes Bronkhorst, a Thomas Burke, a Henry Cohn, a Paul Dundas, a Matthew Emerton, a Harry Falk, a Martin Gardner, a Nina Goldmakher, a Susan Goldstine, a James Gunn, a Raqeeb Haque, a Takao Hayashi, a Michele Jaffe, a James Rex Knowlson, a Takeschi Kukobo, a Richard Landes, a Boris Lietsky, a Rhea MacDonald, a Georg Moser, a Charles Napier, a Lena Nekludova, a David Nelson, a Katsumi Nomizu, a Yori Oda, a Larry Pfaff, a Donald Rance, a Andrew Ranicki, a Aamir Rehman, a Abdulhamid Sabra, a Brian A. Sullivan, a Daniel Tenney III, a Alf van der Poorten, a Jared Wunsch, a Michio Yano e a Don Zagier.

Infine, non so come ringraziare, per il sostegno che non mi hanno fatto mai mancare quando più ne avevo bisogno, i Kaplan scozzesi, Tomás Guillermo, i Gilligan e i Klubock di Cambridge, gli Harrison-Mahdavi di Parigi, i Franklin del Wiltshire, i Nuzzo di Chestnut Hill, gli Zelevinsky di Sharon – e tutti i miei studenti.

LA LENTE

Guardate lo zero, e vedrete niente; guardate attraverso lo zero, e vedrete il mondo. Infatti, esso consente di mettere a fuoco il maestoso, organico sviluppo della matematica, e questa, a sua volta, la natura complessa della realtà. Dal contare al calcolare, dai pronostici alla previsione dei cicli economici più propizi alle attività di ciascuno, i brillanti strumenti della matematica ci permettono di comprendere come, bordeggiando, i fenomeni seguano rotte che si determinano a vicenda, e tutti gl’ingranaggi ruotino intorno al più piccolo dei perni: lo zero.

Questi strumenti mentali rendono visibili le intime leggi che governano gli oggetti intorno a noi, nei loro cicli e nelle loro improvvise deviazioni. La stessa mente umana si rispecchia nella matematica, generando immagini virtuali potenzialmente illimitate, che ora confondono ora illuminano il nostro pensiero.

L’itinerario temporale e concettuale dello zero è pieno di complicazioni, travestimenti e scambi di persona, come le vite degli esploratori che lo introdussero in Occidente. In questo libro lo vedrete comparire per la prima volta al tempo dei Sumeri, quasi come un ripensamento; scomparire, tornare e trasformarsi in modo pressoché casuale nei secoli seguenti. La sua potenza sembrerà divina ad alcuni, diabolica ad altri. In Grecia esso farà capolino e subito scomparirà come un dio capriccioso. In India esso soggiornerà a lungo tra gli uomini, a proprio agio e con una sorta di peculiare nonchalance. Giunto in Occidente, sarà coinvolto nelle crisi d’identità della nostra cultura, per emergere su questo versante della rivoluzione newtoniana con tutte le sottigliezze e le complessità del tempo presente.

Nei confronti di queste vicissitudini il mio approccio sarà in parte quello del naturalista, preoccupato di raccogliere e classificare la bella varietà di forme assunta dallo zero – non solo in quanto numero, ma in quanto metafora di gioia e disperazione; in quanto niente che nel contempo è qualcosa; in quanto progenitore di noi tutti e mistero dei misteri. Ma noi, che non siamo semplici gazze, non foderiamo i nostri nidi con piume ma con briciole di tempo. Perciò fin dall’inizio la prospettiva storica si aggiungerà a quella naturalistica, dandoci la possibilità di gustare la descrizione di chi, con abilità di giocoliere, fece danzare numeri di grandezza inaudita; di chi si ritrovò con la vita appesa al filo di un calcolo; e di eventi il cui corso maestoso tra Oriente a Occidente trasportò seco lo zero – nonché del modo in cui quegli eventi furono influenzati da personalità che s’imprimono nella nostra memoria ora per la vitalità ora per l’eccentricità, come l’esile mercante pisano o il gentiluomo scozzese convinto di essere uno stregone.

Addentrandoci nei meandri dei simboli e dei sensi dello zero vedremo scorrere davanti ai nostri occhi l’evoluzione della matematica, impresa d’uomini a beneficio di altri uomini. Nessun dio ce l’ha regalata. La sua musa dà ispirazione solo a quelli che la desiderano veramente. E come si manifesta il suo intervento? In più di un modo: come un mélange di fulminee illuminazioni e umile indaffararsi; come un’idea trovata da qualcuno, caduta in un sonno secolare e risvegliatasi all’improvviso in climi intellettuali del tutto diversi; o ancora, come un prolungato dialogo tra intuizione e verifica razionale, tra fantasia e logica.

Perché mai lo zero – quest’O senza figura, come Shakespeare l’ha chiamato – ha avuto un ruolo così decisivo nella tessitura della grande trama di espressioni che chiamiamo «matematica»? Perché la maggior parte degli specialisti di questa disciplina gli assegna un posto d’onore in ogni elenco dei numeri più importanti? Come si è arrivati a sostenere che se 0 x 0 = 0, allora i numeri sono reali? Troveremo le risposte ripercorrendo l’evoluzione dello zero.

E osservando lo zero e la matematica crescere insieme, metteremo a fuoco istanze più profonde all’interno della nostra mente. Per esempio, il nostro curioso bisogno di attribuire nomi a ciò che creiamo, per poi chiederci se le creature esistano indipendentemente dai loro nomi. E il bisogno opposto, ma altrettanto pressante, di distanziarci ancora di più da individui e casi particolari, sempre all’inseguimento di ciò che è generale, sempre pronti a sussumere la singolarità delle cose in serie escheriane, a preferire la visione panoramica del frutteto al singolo albero nodoso.

Sotto queste correnti del nostro pensiero riusciremo a intravedere, nel succedersi dei capitoli, i flussi ancora più lenti e sotterranei che ci spingono ora a osservare il mondo, ora a spingere lo sguardo al di là di esso. L’inquietante interrogativo se lo zero sia «là fuori» o una pura creazione della mente umana porta con sé l’eterno quesito se il corso dei fenomeni sia qualcosa che scopriamo o inventiamo, quindi quello ancor più profondo circa il nostro posto nella grande gerarchia: siamo creature o creatori? Molto o appena al di sotto degli angeli, nella nostra capacità di comprendere ciò che ci circonda?

La matematica è un’attività che si esercita su ogni attività. Il suo cammino non è concluso; anzi, è appena cominciato, nonostante la politezza dei suoi risultati conferisca loro qualcosa di monumentale, e la storia dello zero vi imprima il marchio di ciò che è compiuto. Ma lo zero non è omologabile al chiudersi di una circonferenza. Semmai, esso delimita un passaggio. Uno dei più lungimiranti matematici del nostro tempo, Alexander Grothendieck, i cui contributi hanno cambiato la nostra stessa percezione della matematica, dedicò anni e anni al suo magnum opus. Corresse, ampliò, il libro intero e la sua prefazione/compendio, il Capitolo 0. Ora sappiamo che né l’uno né l’altra saranno mai portati a termine. Sempre più prossimo, quasi a portata di mano, ma mai realmente afferrabile: è questa, forse, la definizione meno inadeguata dell’intima natura dello zero.

CAPITOLO 1

La mente imprime il suo marchio alla materia

Zero ha cominciato la sua carriera sotto forma di due cunei in un mucchio di argilla fresca, al tempo in cui un superbo esempio di ingegneria mentale ci ha regalato l’arte di contare. E contare, in fondo, significa questo: associare specifici sostantivi numerici, e simboli specifici, a raccolte di oggetti di forma differente: uno, due, tre... Ma se continuassimo ad attribuire nomi e simboli nuovi a ogni nuova raccolta, ben presto ci troveremmo a corto sia di fantasia che di memoria. Provate a inventare simboli diversi per i primi 20 numeri, per esempio:

e poi chiedetevi: quanto fa sette più otto? Allora... Dovrebbe fare V.

E Ψ meno / ? Vediamo... Contando all’indietro / posti a partire da Ψ si ottiene 6.

E γ più ∧? Questa volta siamo nei guai; non abbiamo ancora inventato un simbolo per questo numero, e se decidessimo di farlo dovremmo prima escogitarne altri sette.

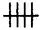
dp n="18" folio="18" ?

Il modo di superare questa impasse sembra esser stato scoperto molto presto in tutte le culture, così come compare precocemente nella vita del bambino. Si riuniscono gli oggetti che si desidera contare in gruppi della medesima grandezza – una grandezza comoda, alla quale si è dato un nome; e si contano i gruppi, invece degli oggetti singoli. Per esempio:

I gruppi più comuni tendono a consistere in cinque o dieci elementi, per via delle dita delle nostre mani, ma qualunque numero che si riconosce a colpo d’occhio può andar bene (le uova si contano a dozzine).

Tuttavia, appena trovata questa scorciatoia (che comporta un ulteriore, significativo passo avanti: l’aggiunta della moltiplicazione all’addizione) subito si è costretti a cercarne un’altra. Se corrisponde a

volte

con l’aggiunta di

, che numero è questo, precisamente? Alla fine, sembra che la necessità di introdurre un nuovo nome e un nuovo simbolo sia stata solo rimandata. A quest’ostacolo, culture diverse hanno reagito in modi diversi. Prendendo lo spunto forse dall’uso di barrare alcune tacche sulle asticciole per calcoli, forse da segnali fatti con le mani nei mercati, i Romani hanno assegnato X a

, V a

(tra l’altro, «V» è la metà superiore di «X» e corrisponde alle dita di una mano sola). Ne deriva che «XV», scritto da sinistra a destra per analogia con le parole, vale 3 volte «V». Invece degl’ingombranti VVVV o XVV per quattro 5, i Romani scrivevano XX: due 10.

Perciò la nostra addizione è diventata:

X + XVIII = XXVIII.

L’idea sembra promettente, ma mostrerà i suoi limiti appena comincerete a stancarvi di scrivere interminabili serie di X ogni volta che un numero è grande. Ancora una volta, si rischia di dover introdurre in continuazione nuovi simboli per indicare numeri sempre maggiori. I Romani usavano L per 50; perciò LX significava 10 dopo 50, cioè 60, e XL significava 10 prima di 50, cioè 40. C corrispondeva a 100, D a 500, M a 1000 e infine, col crescere di debiti, crediti e patrimoni fu introdotta una cornice aperta verso il basso, che tracciata intorno a un numero moltiplicava il suo valore per 100.000. Così, Livia lasciò 50.000.000 di sesterzi a Galba ma suo figlio, l’imperatore Tiberio, amico di pochi e certamente non di Galba (nonché erede del rimanente dei beni di sua madre), sostenne che

andava letto D. I sesterzi erano diventati in un sol colpo 500 quia notata non perscripta erat summa, «perché la somma non era scritta in lettere ma in numero». Proprio il tipo di spiegazione che c’è da attendersi da un imperatore.

dp n="20" folio="20" ?

D’altronde, quel modo di contare creava problemi nella vita di ogni giorno, non solo negli uffici dei grandi avvocati.

Quanto fa 43 + 24? Per i Romani, il problema era: quanto fa XLIII + XXIV?

Nessun tentativo di incolonnare questi numeri produrrà automaticamente la r...

Indice dei contenuti

• Copertina
• Frontespizio
• Zero. Storia di una cifra