Il disordine perfetto

L'avventura di un matematico nei segreti della simmetria

Marcus Du Sautoy

• Editore: BUR
• Anno: 2011
• Print ISBN: 9788817039000
• eBook ISBN: 9788858600610
• Argomento: Biological Sciences
• Categoria: Science General

Nel Giovedì Santo del 1770 il quattordicenne Mozart si trovava a Roma, dove ascoltò il Miserere di Allegri: un corale che poteva essere eseguito solo nella Cappella Sistina durante la Settimana Santa, e del quale non circolavano gli spartiti. Ne rimase profondamente colpito, tanto da volerne riscrivere - a mente - l'intera partitura a nove voci. Fu solo la sua prodigiosa memoria a rendere possibile l'impresa? Marcus du Sautoy mostra come quel "miracolo" fu in realtà una conseguenza della straordinaria capacità di Mozart di cogliere la struttura logica interna della composizione, di catturarne la simmetria e sfruttarla per ricostruire il pezzo a partire dagli elementi che ricordava. Questo è solo un esempio della potenza della simmetria, che dalle molecole di carbonio ai virus, dai codici informatici alla mente umana - programmata per cercarne ovunque le tracce - sembra essere una caratteristica della realtà. Un viaggio in un mondo affascinante e pieno di sfaccettature che è, al contempo, un viaggio nell'avvincente lavoro svolto dalla matematica per comprendere la regola segreta dell'universo.

1
Agosto: fini e inizi

L’universo è costruito su una pianta la cui profonda simmetria è in qualche modo presente nella struttura interiore del nostro intelletto.

Paul Valéry

Mezzogiorno, 26 agosto, deserto del Sinai

È il mio quarantesimo compleanno. Ci sono 40 gradi. Sono cosparso di crema solare con fattore di protezione 40, riparato all’ombra di una baracca su una sponda del Mar Rosso. L’Arabia Saudita scintilla oltre l’acqua azzurra. Al largo, le onde si frangono dove la barriera corallina digrada verso il fondale. I monti del Sinai torreggiano alle mie spalle.

Di solito non mi preoccupo granché dei compleanni, ma, per un matematico, compiere quarant’anni significa aver raggiunto una tappa significativa e non per via di una numerologia arcana e bizzarra, bensì per la diffusa convinzione secondo cui a quest’età ormai la maggior parte del proprio lavoro è stato svolto. La matematica, si dice, è roba da giovani. La medaglia Fields, il più prestigioso riconoscimento di questa disciplina, viene assegnata, con cadenza quadriennale, solo a matematici sotto i quarant’anni. L’anno prossimo, in questo periodo, annunceranno l’ultima tornata di vincitori a Madrid, ma ormai sono troppo vecchio per sperare di essere nella lista. Ora che ho trascorso tutto questo tempo a girovagare per i giardini della matematica, il Sinai non è forse un luogo sinistro in cui trovarmi: un arido deserto dove una nazione in esilio vagabondò per quattro decenni?

Da bambino non volevo fare il matematico. Avevo deciso di studiare lingue all’università; quella mi pareva essere la strada da percorrere per realizzare il mio sogno più grande: diventare una spia. Prima di sposarsi, mia madre aveva lavorato al ministero degli Esteri. Negli anni Sessanta, il corpo diplomatico riteneva che la maternità fosse incompatibile con quel tipo di professione, così si era licenziata. Ma, a suo dire, le avevano permesso di tenere la piccola rivoltella nera che ogni dipendente del dicastero doveva portare. «Non sai mai quando possono richiamarti per un incarico segreto all’estero» spiegava, enigmatica. La pistola, sosteneva, era nascosta da qualche parte a casa nostra.

L’avevo cercata ovunque, ma evidentemente erano stati molto meticolosi quando avevano insegnato alla mamma l’arte dell’occultamento. L’unico modo per procurarmi un’arma era entrare a mia volta nel ministero degli Esteri e diventare una spia. E, se volevo riuscirci, avrei fatto meglio a imparare il russo.

Seguivo tutti i corsi di lingua che si tenevano nella mia scuola: francese, tedesco, greco e latino. La BBC aveva cominciato a trasmettere un corso di russo in televisione. Tuttavia, non avevo mai convinto la mia bocca a pronunciare correttamente la parola zdravstvuyte (ciao), nemmeno dopo otto settimane di lezioni. Iniziai a disperare e a sentirmi frustrato: non scorgevo alcuna logica dietro le coniugazioni di alcuni verbi stranieri e dietro la suddivisione dei sostantivi in maschili e femminili. Solo il latino offriva qualche speranza, con la sua rigida grammatica capace di appagare il mio nuovo desiderio di cose che appartenessero a uno schema logico e coerente e non fossero soltanto associazioni all’apparenza casuali. O forse dipendeva dal fatto che il professore usava sempre il mio nome per i sostantivi della seconda declinazione: Marcus, Marci, Marco, Marcum…

Un giorno, all’età di dodici anni, l’insegnante di matematica mi indicò e in tono perentorio mi disse: «Du Sautoy, vieni da me alla fine della lezione». Credetti di essere nei guai. Lo seguii fuori dall’aula e, quando fummo in giardino, estrasse un sigaro dalla tasca e lo accese con lentezza. Quindi mi disse: «Credo che dovresti scoprire cos’è davvero la matematica».

Non so ancora perché, fra tutti gli studenti della classe, avesse scelto proprio me per quella rivelazione. Ero lungi dall’essere un genio della matematica e molti dei miei compagni sembravano altrettanto bravi in quella materia, ma evidentemente qualcosa aveva indotto il signor Bailson a pensare che forse avessi voglia di vedere cosa vi fosse oltre l’aritmetica insegnata a scuola.

Mi consigliò di leggere la rubrica di Martin Gardner sullo «Scientific American». Mi suggerì un paio di libri che, a suo avviso, mi sarebbero potuti piacere, tra cui The Language of Mathematics di Frank Land. Il semplice fatto che un professore avesse dimostrato un interesse personale nei miei confronti bastò a spronarmi ad appurare cosa ci trovasse di tanto affascinante in quella disciplina.

Quel week-end, io e mio padre facemmo una gita a Oxford, la città universitaria più vicina a casa nostra. Un negozietto di Broad Street recava l’insegna Blackwell. Da fuori non pareva molto promettente, ma qualcuno aveva detto a papà che era la Mecca delle librerie accademiche. Entrando, capivi il perché. Come il Tardis di Doctor Who, oltre la minuscola porta il locale era enorme. I volumi di matematica, ci informarono, erano nella Norrington Room, vale a dire il seminterrato.

Mentre scendevamo al piano di sotto, ci si aprì davanti una vasta sala cavernosa, zeppa di quelli che mi parvero tutti i possibili libri scientifici mai pubblicati. Era una grotta di Aladino piena di testi. Mentre mio padre cercava i titoli suggeriti dal signor Bailson, cominciai a estrarre i volumi dai ripiani e a sbirciarvi dentro. Gli indici parevano straordinari. Riconobbi stringhe di caratteri greci grazie alla mia breve incursione nello studio di quella lingua. Vi erano scrosci di minuscoli numeri e lettere che ornavano le x e le y. Su ogni pagina comparivano parole in neretto come Lemma e Dimostrazione.

Per me non avevano alcun senso. Appoggiati agli scaffali, alcuni studenti leggevano quei libri come se fossero romanzi. Ovviamente comprendevano quel linguaggio. Era soltanto un codice. In quel momento decisi di imparare a decifrare quei geroglifici matematici. Mentre pagavamo alla cassa, scorsi un tavolo traboccante di tascabili dalla copertina gialla. «Sono riviste matematiche» spiegò il commesso. «Gli editori ne offrono copie gratuite per indurre gli accademici ad abbonarsi.»

Presi un campione intitolato «Inventiones Mathematica» e lo infilai nel sacchetto dei testi che avevamo appena acquistato. Ecco la mia sfida. Sarei riuscito a decodificare le invenzioni matematiche descritte in quel libretto? Alcuni articoli erano in tedesco, uno in francese e gli altri in inglese. Quello che ora ero determinato a penetrare era tuttavia il linguaggio matematico. Cos’erano uno «spazio di Hilbert» e un «problema di isomorfismo»? Quale messaggio si nascondeva tra quelle righe di sigma, delta e simboli di cui non conoscevo neppure il nome?

Quando arrivai a casa, iniziai a sfogliare i volumi. The Language of Mathematics era quello che mi incuriosiva di più. Prima della spedizione a Oxford non avevo mai pensato alla matematica come a un linguaggio. Quella insegnata a scuola sembrava consistere solo di numeri da moltiplicare o dividere, sommare o sottrarre, con vari gradi di difficoltà. Consultando quell’opera, capii tuttavia perché il mio insegnante mi aveva invitato a «scoprire cos’è davvero la matematica».

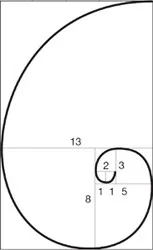
In quelle pagine non vi erano divisioni fra numeri con molte cifre decimali o cose simili. Si trovano invece, per esempio, importanti sequenze di numeri, come quella di Fibonacci, capace, affermava il testo, di spiegare la crescita dei fiori e delle conchiglie. Ciascun componente della serie si otteneva addizionando i due precedenti. La sequenza cominciava con 1, 1, 2, 3, 5, 8, 13, 21, … Secondo Land, quei numeri erano come un codice in grado di indicare alla conchiglia cosa fare man mano che si sviluppava. Si formava un minuscolo mollusco con una casetta di 1 × 1 centimetri quadrati. Poi, ogni volta che l’animaletto diventava più grande del guscio, aggiungeva un’altra stanza alla costruzione. Non avendo molto su cui basarsi, si limitava a creare uno spazio le cui dimensioni fossero la somma di quelle dei due precedenti. Il risultato di quel processo semplice e bellissimo era una spirale (figura 1.1). Sul libro c’era scritto che quei numeri erano fondamentali per il modo in cui la natura faceva crescere qualunque cosa.

Sfogliandolo, mi imbattei in interessanti oggetti tridimensionali che non avevo mai visto prima, formati da pentagoni e triangoli. Uno si chiamava «icosaedro» e aveva 20 facce triangolari (figura 1.2). A quanto pareva, se si prendeva una di quelle forme (che il libro chiamava poliedri) e si contavano le facce e le punte (che il libro chiamava vertici), sottraendo poi il numero di bordi, si otteneva sempre due. Per esempio, un cubo aveva 6 facce, 8 vertici e 12 bordi: 6 + 8 − 12 = 2. Secondo Land, quel trucco avrebbe funzionato per qualsiasi poliedro. Assomigliava a un gioco di prestigio. Lo provai sul solido composto da 20 triangoli.

Figura 1.1: Il mollusco usa i numeri della sequenza di Fibonacci per ampliare la conchiglia.

Figura 1.2: L’icosaedro con 20 facce triangolari.

Il difficile però stava nell’immaginare l’intero oggetto con chiarezza sufficiente per contare tutto. Anche se ne avessi costruito uno di cartoncino, calcolare tutti quei bordi sembrava un po’ scoraggiante. Ma poi mio padre mi indicò una scorciatoia. «Quanti triangoli ci sono?» Be’, il volume diceva 20. «Allora fanno 60 bordi su 20 triangoli, ma ogni bordo è condiviso da due triangoli. Dunque, i bordi sono 30.» Ebbene, quello sì che era un gioco di prestigio. Era possibile sapere quanti bordi aveva l’icosaedro senza nemmeno guardarlo. Lo stesso stratagemma valeva per i vertici. Di nuovo, 20 triangoli hanno 60 vertici. Ma questa volta vidi nella figura che ciascuno era condiviso da cinque triangoli. Perciò l’icosaedro aveva 20 facce, 12 vertici e 30 bordi. E naturalmente, 20 + 12 − 30 = 2. Ma perché la formula funzionava a prescindere dal poliedro scelto?

In un altro testo vi era un intero paragrafo sulla simmetria di oggetti come quei poliedri fatti di triangoli. Avevo una vaga idea di cosa significasse «simmetria». Sapevo di essere simmetrico, almeno all’esterno. Qualunque cosa avessi sul lato sinistro del corpo, ve n’era un’immagine speculare sul destro. Ma un triangolo, pareva, aveva una simmetria molto più marcata di quella semplicemente speculare. Potevi anche ruotarlo, e restava sempre uguale. Cominciai ad accorgermi di non essere davvero sicuro di cosa volesse dire che una cosa era simmetrica.

Secondo il libro, il triangolo equilatero aveva sei simmetrie. Continuando a leggere, iniziai a capire che la simmetria di quel poligono era racchiusa nelle alterazioni cui potevo sottoporlo senza modificarne l’aspetto. Disegnai un profilo intorno a un pezzo di cartoncino triangolare, quindi contai i modi in cui potevo variare la figura cosicché rientrasse esattamente nella sagoma sul foglio. Ciascuna di quelle mosse, affermava il libro, era «una simmetria» del triangolo. Dunque la simmetria era qualcosa di attivo, non di passivo. Gli autori mi spinsero a concepirla come un’azione da effettuare sul triangolo per ricollocarlo dentro il suo contorno anziché come una proprietà intrinseca del poligono stesso. Cominciai a contare le simmetrie della figura, cioè i vari interventi cui potevo sottoporla. Potevo ribaltarla in tre modi. Ogni volta, due angoli si scambiavano di posto. Potevo anche farle fare 1/3 di rotazione completa, in senso orario o antiorario. Così arrivavo a cinque simmetrie. Qual era la sesta?

Cercai disperatamente ciò che mi era sfuggito, tentando di combinare le operazioni per vedere se riuscissi a individuarne un’altra. Dopo tutto, eseguire due di quelle azioni in sequenza era come effettuarne una sola. Se una simmetria era un intervento capace di rimettere il triangolo dentro la sua sagoma, forse avrei trovato una mossa o simmetria aggiuntiva. E se avessi ribaltato il poligono e poi l’avessi ruotato? No, quella manovra era identica agli altri capovolgimenti. E se l’avessi rovesciato, girato e poi rovesciato di nuovo? No, avrei solo provocato la rotazione nell’altro senso, che avevo già contato. Avevo identificato cinque operazioni, ma qualunque combinazione provassi, non riuscii a scoprire nulla di nuovo. Così tornai al libro.

Compresi che gli autori consideravano come simmetria anche l’opzione di lasciare il triangolo dov’era. Strano… A mio parere il termine «simmetria» indicava qualunque operazione si potesse compiere sul poligono cosicché quest’ultimo restasse dentro il suo profilo, ma ben presto mi resi conto che andava presa in considerazione anche la possibilità di non toccarlo affatto (oppure il gesto equivalente di sollevarlo e rimetterlo esattamente allo stesso posto).

L’idea della simmetria mi piaceva. Le simmetrie di un oggetto mi ricordavano le fasi di un numero di illusionismo. Il matematico ti mostra il triangolo, quindi ti prega di voltarti. Mentre non guardi, gli fa qualcosa. Ma quando ti giri, il poligono è identico a prima. Si può concepire la simmetria complessiva di un oggetto come l’insieme delle manovre che il matematico potrebbe eseguire per convincere qualcuno di non averlo nemmeno sfiorato.

Provai quella nuova magia su altre forme. Eccone qui una interessante, simile a una stella marina con sei punte (figura 1.3). Non potevo capovolgerla senza farla sembrare diversa: pareva ruotare in un solo senso, il che ne distruggeva la simmetria speculare. Ma potevo sempre girarla. Con i suoi sei tentacoli, mi consentiva cinque rotazioni, oltre alla possibilità di lasciarla dov’era. Sei simmetrie. Proprio come il triangolo.

Figura 1.3: Una stella marina a sei punte senza simmetria di riflessione.

Ciascun oggetto aveva il medesimo numero di simmetrie. Il libro parlava tuttavia di un linguaggio in grado di articolare e dare significato all’affermazione: «Questi due oggetti hanno simmetrie differenti». Un linguaggio in grado di svelare perché quei corpi rappresentavano due specie distinte nel mondo della simmetria. Quel codice, prometteva il testo, era anche capace di riconoscere quando due oggetti diversi sul piano fisico erano, in realtà, identici su quello simmetrico. Era proprio il viaggio che stavo per intraprendere: la scoperta della vera natura della simmetria.

Man mano che continuavo a leggere, le forme e le illustrazioni cedevano il passo ai simboli. Ecco il codice cui alludeva il titolo della prima opera. Pareva che esistesse un metodo per tradurre le immagini in linguaggio. Mi imbattei in alcuni dei simboli che avevo scorto nella pubblicazione dalla copertina gialla. Tutto iniziava a diventare piuttosto astratto, ma sembrava che quella lingua cercasse di esprimere la scoperta che avevo fatto giocando con le sei simmetrie del triangolo. Se si prendevano due simmetrie, o mosse da prestigiatore, e si effettuavano l’una dopo l’altra, per esempio una riflessione seguita da una rotazione, se ne otteneva una terza. Il linguaggio che descriveva quelle interazioni aveva un nome: teoria dei gruppi.

Quel codice spiegava perché le sei simmetrie della stella marina a sei punte erano diverse dalle sei del triangolo. Una simmetria era una di quelle operazioni magiche, perciò potevo compierne due in successione per averne una terza. Le interazioni nel gruppo di simmetrie della stella marina erano molto diverse da quelle nel gruppo del triangolo. A distinguere un oggetto dall’altro erano pertanto i rapporti all’interno degli insiemi di simmetrie.

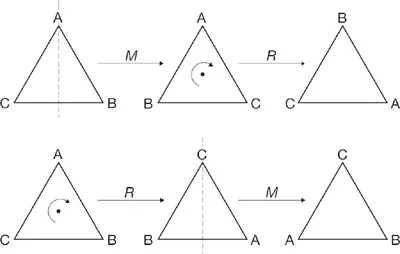
Nella stella marina, per esempio, una rotazione seguita da una seconda rotazione me ne dava una terza. L’ordine in cui eseguivo i due interventi non aveva tuttavia alcuna importanza. Girando pertanto l’oggetto di 180° in senso orario e poi di 60° in senso antiorario, lo portavo nella medesima posizione in cui l’avrei portato invertendo le due azioni. Invece, se prendevo due simmetrie del triangolo e combinavo i due trucchi illusionistici corrispondenti, l’ordine in cui li effettuavo faceva una notevole differenza. Un’operazione di simmetria speculare seguita da una rotazione non era uguale alla rotazione seguita dall’operazione di simmetria speculare. Il linguaggio del libro aveva tradotto le illustrazioni nella frase M × R ≠ R × M, dove M era la mossa di simmetria speculare ed R la rotazione (figura 1.4). Era possibile tradurre il mondo fisico della simmetria in un linguaggio algebrico astratto.

Figura 1.4: Una simmetria speculare seguita da una rotazione è diversa da una rotazione seguita da una simmetria speculare.

Proseguendo gli studi, riuscii a capire cos’aveva fatto il mio professore di matematica. L’aritmetica insegnata in aula è un po’ come le scale e gli arpeggi per un musicista. Il signor Bailson mi aveva suonato alcuni degli appassionanti brani che mi avrebbero aspettato là fuori se fossi riuscito a padroneggiare la parte tecnica dell’argomento. Non comprendevo certo tutto ciò che leggevo, ma ora volevo saperne di più.

Quasi tutti i musicisti in erba abbandonerebbero la loro arte se fossero costretti a suonare e ascoltare soltanto scale e arpeggi. Un bambino che si accosta all’uso di uno strumento non ha idea di come Bach a...

Indice dei contenuti

• Cover
• BUR
• Frontespizio
• 1. Agosto: fini e inizi
• 2. Settembre: il successivo lancio del dado
• 3. Ottobre: il palazzo della simmetria
• 4. Novembre: raduno tribale
• 5. Dicembre: nessi inaspettati
• 6. Gennaio: impossibilità
• 7. Febbraio: rivoluzione
• 8. Marzo: forme indivisibili
• 9. Aprile: simmetria sonora
• 10. Maggio: applicazioni
• 11. Giugno: sporadicità
• 12. Luglio: riflessioni
• Ringraziamenti
• Bibliografia
• Crediti delle immagini
• Indice