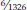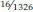Il poker non è più quello di una volta. Il vecchio poker era passivo e attendista, un gioco basato principalmente su buone carte di partenza. Oggi invece il Texas Hold'Em è un gioco ricco di azione dove per vincere serve tanta abilità. Questo libro aiuta a vedere il gioco sotto un'altra prospettiva. Tanti consigli o giocate che sembravano giusti sono rapidamente diventati sbagliati. Molto sbagliati. Giocare chiusi in attesa di carte forti è diventata una strategia perdente. Il gioco è bello perché non sempre vince la mano migliore di partenza. La via del successo passa oggi attraverso l'aggressività. Vincere senza girare le carte è un'arma potente e necessaria. Questo gioco non è più vissuto come - ore di noia e attimi di terrore -, bensì si cerca di costruire piccoli vantaggi ripetuti nel tempo. E basta con tanti vecchi libri che sembrano fermi all'epoca in cui si puntavano orologi d'oro e si ricevevano pallottole! Raccontano un gioco che non esiste più. Con questo libro, fondato sulla lunga esperienza mia e di altri giocatori che hanno prestato la loro prestigiosa collaborazione, vogliamo guidarvi nel mondo del Nuovo Poker. Spiegheremo punto per punto perché, dove, cosa, quanto e quando giocare. Ma soprattutto come giocare e vincere, servendosi della matematica e della psicologia. E alla fine vi verrà voglia di giocare contro chi ha letto troppi vecchi libri! Flavio Ferrari Zumbini
Domande frequenti
Sì, puoi annullare l'abbonamento in qualsiasi momento dalla sezione Abbonamento nelle impostazioni del tuo account sul sito web di Perlego. L'abbonamento rimarrà attivo fino alla fine del periodo di fatturazione in corso. Scopri come annullare l'abbonamento.
Al momento è possibile scaricare tramite l'app tutti i nostri libri ePub mobile-friendly. Anche la maggior parte dei nostri PDF è scaricabile e stiamo lavorando per rendere disponibile quanto prima il download di tutti gli altri file. Per maggiori informazioni, clicca qui.
Perlego offre due piani: Base e Completo
Base è ideale per studenti e professionisti che amano esplorare un’ampia varietà di argomenti. Accedi alla Biblioteca Base con oltre 800.000 titoli affidabili e best-seller in business, crescita personale e discipline umanistiche. Include tempo di lettura illimitato e voce Read Aloud standard.
Completo: Perfetto per studenti avanzati e ricercatori che necessitano di accesso completo e senza restrizioni. Sblocca oltre 1,4 milioni di libri in centinaia di argomenti, inclusi titoli accademici e specializzati. Il piano Completo include anche funzionalità avanzate come Premium Read Aloud e Research Assistant.
Entrambi i piani sono disponibili con cicli di fatturazione mensili, ogni 4 mesi o annuali.
Perlego è un servizio di abbonamento a testi accademici, che ti permette di accedere a un'intera libreria online a un prezzo inferiore rispetto a quello che pagheresti per acquistare un singolo libro al mese. Con oltre 1 milione di testi suddivisi in più di 1.000 categorie, troverai sicuramente ciò che fa per te! Per maggiori informazioni, clicca qui.
Cerca l'icona Sintesi vocale nel prossimo libro che leggerai per verificare se è possibile riprodurre l'audio. Questo strumento permette di leggere il testo a voce alta, evidenziandolo man mano che la lettura procede. Puoi aumentare o diminuire la velocità della sintesi vocale, oppure sospendere la riproduzione. Per maggiori informazioni, clicca qui.
Sì! Puoi usare l’app Perlego sia su dispositivi iOS che Android per leggere in qualsiasi momento, in qualsiasi luogo — anche offline. Perfetta per i tragitti o quando sei in movimento. Nota che non possiamo supportare dispositivi con iOS 13 o Android 7 o versioni precedenti. Scopri di più sull’utilizzo dell’app.
Sì, puoi accedere a Il nuovo poker di Flavio Ferrari Zumbini in formato PDF e/o ePub. Scopri oltre 1 milione di libri disponibili nel nostro catalogo.
“Se pensate che la matematica nel poker non sia importante, allora non conoscete la matematica giusta” è un’affermazione che si sente spesso nel mondo del poker. Non troverete un solo giocatore di successo che reputi inutile conoscere quantomeno le basi della matematica del gioco.
Dalla matematica non si può prescindere, bisogna fare amicizia con i concetti di questo capitolo. Tuttavia, se state pensando di dover rispolverare (o studiare da zero) formule astruse, se pensate di imbattervi in principi che vi faranno venire il mal di testa, potete dormire sonni tranquilli. Tutto quello che serve è saper contare fino a 13 ed essere in grado di fare moltiplicazioni per 2 e per 4!
7.1. Perché serve la matematica nel poker?
Che ci piaccia o no, questo gioco è governato dall’aritmetica, dalle leggi statistiche e dal calcolo delle probabilità. In una parola, dalla matematica. Non se ne esce. Si può anche pensare di essere la persona più intelligente (o magari fortunata) del mondo, ma prima o poi senza il supporto della matematica si smetterà di vincere.
7.2. Probabilità delle mani iniziali
Il primo, piccolo passo in avanti è imparare a contare come si combinano le carte del mazzo per formare le mani iniziali che ci vengono servite.
Perché serve saperlo? Una delle cose che distingue un giocatore forte da un principiante è certamente la capacità di riuscire a farsi un’idea di cosa possa avere in mano l’avversario, un’idea che sarà basata su tutte le possibili informazioni a disposizione.
Tra le cose da sapere c’è, ovviamente, la probabilità che l’avversario abbia una certa mano piuttosto che un’altra. Sapere, ad esempio, che tutti i possibili AK sono tanti quasi quanto tutti gli AA, KK e QQ messi insieme ci aiuterà a prendere la decisione migliore.
Non è necessario imparare a memoria tutti i numeri delle combinazioni di carte. È sufficiente ricordare i punti cardine dei ragionamenti.
7.2.1. Come contare le combinazioni
Un mazzo è formato da 52 carte, ha 4 semi e 13 carte per tipo in ogni seme. Di queste, due vengono date a ogni giocatore. Fin qui tutto molto ovvio.
Ora, sapere le combinazioni iniziali è piuttosto semplice: basta ricordare come è composto un mazzo di carte e fare pochi conti, nel senso proprio di contare.
Iniziamo con la mano preferita da tutti: AA. Ci sono 4 Assi nel mazzo, uno per ogni seme. Se si contano le possibili coppie di due semi si scopre che sono 6: Picche-Cuori, Picche-Quadri, Picche-Fiori, Cuori-Quadri, Cuori-Fiori e Quadri-Fiori (ovviamente non conta l’ordine dei due semi, la mano AhAc è identica a AcAh*).
Quindi una coppia di Assi può essere servita solo in 6 modi diversi. E se ci sono 6 combinazioni possibili di AA, ce ne saranno altrettante per ogni altra coppia.
Passiamo ad AK. Per ognuno dei 4 Assi ci sono 4 Re, quindi basta moltiplicare 4×4 per scoprire che ci sono un totale di 16 combinazioni di AK. La stessa cosa vale per ogni altra mano specifica che non sia una coppia, le combinazioni sono sempre 16.
E di queste quante sono suited? Facile, AKs si può formare solo con 4 combinazioni, una per ogni seme. Quindi se le combinazioni di AK sono 16 e le combinazioni di AKs sono 4, è facile capire che le combinazioni di AKo* sono 12. Lo stesso vale ovviamente per ogni altra mano non accoppiata.
Questo è tutto quello che c’è da ricordare per le combinazioni di mani iniziali. Passiamo ora alle probabilità.
7.2.2. Probabilità
Ora sappiamo calcolare quante combinazioni ci sono per ogni possibile mano; come facciamo a sapere quanto spesso verrà servita ognuna di esse?
Anche questo è piuttosto facile. Dobbiamo prima sapere che da un mazzo di 52 carte, tutte le combinazioni possibili di mani iniziali sono 1326.
NUMERO DI COMBINAZIONI DI PARTENZA
Perché 1326? Perché è il risultato di 52 x 51 diviso 2. Si può infatti ricevere una qualunque delle 52 carte inizialmente, ma poi solo una delle 51 rimanenti. Il tutto va diviso per 2, perché come detto, l’ordine con cui vengono servite le carte è insignificante. Un numero abbastanza anonimo, si potrebbe pensare. Vero, ma per fortuna non dobbiamo neanche ricordarlo!
A questo punto, basta dividere il numero di combinazioni di ogni tipo di mano per tutte le combinazioni possibili e sapremo quanto spesso ci viene servita quella mano. Proviamo.
Una coppia di Assi ha 6 combinazioni, quindi la probabilità che ci venga servita AA è pari a
. Questo numero equivale a una volta ogni 221 mani, ovvero allo 0,45%, che volendo si può anche arrotondare ottimisticamente a 0,5%, che è più facile da ricordare. In pratica, se giochiamo dal vivo, possono passare molte ore prima di vederci serviti AA!
Per quanto riguarda invece una mano non accoppiata, come AK, la probabilità è pari a
, numero che equivale a 1,2%, ovvero poco meno di una volta ogni 80 mani. Questa percentuale deve essere divisa per 4 se si vuole sapere la probabilità che le due carte siano suited: abbiamo quindi lo 0,3% di avere servita la versione suited di una specifica mano.
• La probabilità di avere una delle 13 possibili coppie è circa 0,5%.
• La probabilità di avere una specifica mano non accoppiata è 1,2%.
• La probabilità di avere una specifica mano suited è 0,3%.
Basta ricordare queste tre percentuali per poter seguire il resto del capitolo.
7.2.3. Blocker
Nel valutare la possibile mano di un avversario, non dobbiamo di certo dimenticare l’informazione che abbiamo nel vedere le nostre carte.
Il numero di combinazioni possibili cambia a seconda di cosa abbiamo in mano noi. Un blocker è una carta in nostro possesso che “blocca”, appunto, alcune combinazioni agli altri.
Il più classico dei blocker è l’Asso. Se noi ne abbiamo uno, le combinazioni possibili di AA in mano all’avversario si dimezzano, passando da 6 a 3. Analogamente AK passa da 16 a 12 combinazioni. Questo tipo di aggiustamento nel calcolo delle probabilità può arrivare ad avere un peso importante nelle nostre scelte.
