Ciò che non possiamo sapere

Avventure ai limitidella conoscenza

Marcus Du Sautoy

• Editore: RIZZOLI
• Anno: 2016
• Print ISBN: 9788817088947
• eBook ISBN: 9788858685969
• Argomento: Computer Science
• Categoria: Computer Science General

Esistono limiti alla conoscenza umana? In un'epoca in cui la scienza sembra darci accesso ai misteri più profondi del mondo fisico, rimane qualcosa che non arriveremo mai a comprendere? In questo suo nuovo saggio Marcus du Sautoy esplora sette confini dello scibile per trovare una risposta a tali interrogativi. Riusciremo mai a stabilire che cos'è la coscienza, a svelare la natura del tempo, ad afferrare i paradossi della meccanica quantistica, a districarci nei meandri della teoria del caos, a scoprire quale destino attende l'universo, a capire se l'infinito è un'entità reale o solo un concetto astratto? Con la chiarezza espositiva e l'arguzia consuete, du Sautoy ci accompagna in un fantastico viaggio di esplorazione dell'ignoto. Ogni tappa comincia da un oggetto semplice – un dado da gioco, un violoncello, un orologio da polso, un piccolo campione di uranio-238 acquistato su internet, un modellino in cartone dell'universo, un'applicazione per smartphone, un bigliettino natalizio – per condurci alle frontiere della ricerca attuale, dove le domande più profonde ci costringono a ragionare non solo di scienza ma anche dell'esistenza di Dio; e a scoprire insieme all'autore che probabilmente non arriveremo mai a conoscere ogni cosa, ma che è proprio questa corsa senza fine verso un traguardo irraggiungibile a dare sempre nuova linfa alla ricerca scientifica e ad alimentare la nostra sete di conoscenza.

Settimo Confine: il cracker natalizio

13

«Il numero è la misura delle forme e delle idee e la causa degli dèi e dei demoni.»

PITAGORA

L’asserzione sull’altra faccia di questa carta è falsa

L’asserzione sull’altra faccia di questa carta è vera

Stanco della solita gamma di cracker natalizi¹ venduti nei negozi, quest’anno ho deciso di preparare per la mia famiglia i miei speciali cracker matematici fatti in casa. Ognuno includeva una barzelletta matematica e un paradosso. Per quanto riguarda le prime, i miei erano dell’opinione che fossero molto più matematiche che non barzellette. Decidete da soli: «Quanti matematici ci vogliono per cambiare una lampadina? 0,9999 periodico». Se non state ridendo, non preoccupatevi; non l’ha fatto neanche la mia famiglia. Se non l’avete capita, il punto è – anche se non bisognerebbe mai spiegare una barzelletta – che si può dimostrare che 0,9999 periodico coincide di fatto col numero 1.

I paradossi erano un pochino meglio. Uno conteneva un nastro di Möbius, un oggetto geometrico in apparenza paradossale che ha un’unica faccia. Se prendete una lunga striscia di carta e le applicate un mezzo giro di torsione prima di incollare insieme le due estremità, la figura che ne risulta ha una faccia sola. Per accertarvene, potete tentare di colorare le facce: iniziate a colorarne una, e presto vi ritrovate ad aver coperto l’intera superficie. Il nastro di Möbius ha poi una proprietà sorprendente: se lo tagliate a metà parallelamente al bordo, non si divide in due anelli separati ma rimane integro, come un singolo anello ma con due mezzi giri di torsione.

Il cracker capitato a me non era troppo male, anche se a dirlo sono io che l’ho preparato. Anche la barzelletta era piuttosto divertente: «Per che cosa sta la “B” in Benoit B. Mandelbrot? Benoit B. Mandelbrot». (Se ancora non state ridendo, forse vi sfugge che Mandelbrot è lo scopritore dei frattali di cui abbiamo parlato nel Primo Confine, quelle forme geometriche che, a qualunque livello di ingrandimento, non diventano mai più semplici.) Il paradosso, poi, era uno dei miei preferiti in assoluto e consisteva delle due asserzioni riportate all’inizio del capitolo, una su ciascun lato di un cartoncino. Sono sempre stato affascinato – e, in egual misura, turbato – dai giochi di parole di questo tipo: da bambino, uno dei miei libri preferiti era intitolato Qual è il titolo di questo libro? ed era pieno di assurdi giochi di parole che spesso sfruttavano, come il titolo, le implicazioni dell’autoreferenzialità.

Ho imparato a non sorprendermi davanti alle frasi formate nel linguaggio naturale che danno origine a paradossi come quello catturato dalla logica circolare delle due asserzioni sul cartoncino del mio cracker: il semplice fatto che possiamo formare frasi dotate di significato non garantisce infatti di assegnare loro valori di verità sensati.

Penso che la natura sfuggente del linguaggio sia una delle ragioni che mi hanno spinto verso le certezze della matematica, dove questa sorta di ambiguità non è tollerata. Come spiegherò in questo confine, però, uno dei più grandi logici matematici di tutti i tempi, Kurt Gödel, si è servito del paradosso del mio cracker per dimostrare che anche la mia stessa disciplina contiene affermazioni sui numeri vere a prescindere dal fatto che noi possiamo mai dimostrarle.

Scienza versus matematica

Il desiderio di certezza, di sapere davvero, è stata una delle ragioni principali per cui ho scelto la matematica rispetto alle altre scienze. Nelle scienze, le cose che pensiamo di sapere sull’universo sono modelli che corrispondono ai dati. Perché una teoria possa considerarsi scientifica, questi modelli devono essere falsificabili, ossia dev’essere possibile dimostrare che, eventualmente, sono sbagliati. Il motivo per cui sopravvivono – se sopravvivono – è che tutti i dati empirici confermano il modello; se e quando scopriamo nuovi dati che lo contraddicono, dobbiamo cambiarlo. Per sua stessa natura, una teoria scientifica può essere scartata. Stando così le cose, potremo mai sapere davvero se siamo nel giusto?

Un tempo pensavamo che l’universo fosse statico, ma poi le nuove scoperte ci hanno rivelato che le galassie si stanno allontanando da noi. Credevamo che l’espansione dell’universo stesse rallentando per via del freno rappresentato dall’attrazione gravitazionale, salvo poi scoprire che sta di fatto accelerando. Abbiamo elaborato un modello di questa espansione accelerata introducendo l’idea che ad alimentarla sia l’energia oscura; questo modello attende ancora di essere falsificato, benché per ora i dati raccolti continuino a corroborarlo. Alla fine, è del tutto possibile che arriveremo al modello corretto dell’universo, che non verrà più smentito da ulteriori rivelazioni; tuttavia, anche in quel caso non potremo mai essere sicuri di essere arrivati alla risposta giusta.

Questo è uno degli aspetti eccitanti della scienza: che si evolve continuamente, ci sono sempre nuove spiegazioni. Possiamo provare un certo dispiacere per le vecchie teorie diventate irrilevanti. Certo, le nuove teorie si sviluppano a partire da quelle vecchie. Uno scienziato vive con la paura che la sua teoria possa essere soltanto la moda del momento, che possa vincere premi su premi per poi ritrovarsi all’improvviso sorpassata. I modelli dell’atomo come un pudding natalizio, l’idea di un tempo assoluto, la convinzione che le particelle avessero una posizione e una quantità di moto identificabili: tutte queste teorie non sono più in cima alla lista dei bestseller della scienza, ma sono state sbaragliate da nuove spiegazioni.

Il modello dell’universo che leggevo sui libri di scuola è stato totalmente riscritto. Lo stesso non si può dire, però, dei teoremi che ho appreso su quei banchi: sono veri oggi come quando li ho incontrati per la prima volta, e come quando sono stati scoperti (in alcuni casi, anche oltre duemila anni fa). Nelle mie vesti di adolescente insicuro e brufoloso, ero davvero attratto dalla certezza promessa da questa disciplina. Ciò non significa che la matematica sia statica: essa continua infatti a crescere man mano che gli ignoti diventano noti, ma con la differenza che questi noti restano tali, continuano a godere di buona salute e diventano le prime pagine nei passi avanti successivi. Perché il processo di acquisizione della verità matematica è così diverso da quello con cui devono fare i conti gli scienziati, che non possono mai sapere con certezza se sono giunti alla verità?

L’ingrediente più importante nell’armamentario del matematico è la dimostrazione.

La dimostrazione: la strada per la verità

Sappiamo che c’erano persone che facevano matematica già nel II millennio a.C.: tavolette di creta babilonesi e papiri egiziani mostrano sofisticati calcoli e soluzioni di enigmi, stime del valore di π, la formula per il volume di una piramide e algoritmi applicati alla soluzione di un’equazione quadratica. In generale, però, questi documenti illustrano procedure applicabili a particolari problemi per ottenere delle soluzioni: non troviamo una giustificazione del motivo per cui queste procedure dovrebbero funzionare sempre, al di là della convincente evidenza che hanno funzionato nelle migliaia di esempi documentati fino a quel momento nelle tavolette di creta. La conoscenza matematica si basava sull’esperienza e aveva un gusto più scientifico; se saltava fuori un nuovo problema che esulava dal corrente algoritmo, le procedure venivano adattate.

Le cose cominciarono a cambiare verso il V secolo a.C., quando gli antichi greci affondarono i denti in questa disciplina. Gli algoritmi iniziarono a essere accompagnati da argomenti che giustificavano la ragione per cui avrebbero fatto sempre ciò che era riportato sulla tavoletta. Non bastava dire che la procedura aveva funzionato nelle ultime mille volte e che quindi avrebbe probabilmente funzionato anche la successiva: l’argomento chiariva perché la proposta avrebbe funzionato sempre. Era nata così l’idea di dimostrazione.

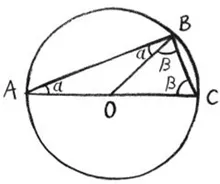
Talete di Mileto è considerato il primo autore accertato di una dimostrazione matematica. Nella fattispecie, ha dimostrato che se prendiamo un punto qualsiasi sulla circonferenza di un cerchio e lo uniamo alle due estremità di una diagonale del cerchio stesso, l’angolo da noi creato è un angolo retto. Non importa quale cerchio o quale punto scegliamo: l’angolo sarà sempre retto. Non è un’approssimazione, e non è così solo perché sembra funzionare in tutti gli esempi che abbiamo tracciato, ma perché è una conseguenza delle proprietà dei cerchi e delle linee.

La dimostrazione di Talete, attraverso una brillante serie di passaggi logici, accompagna il lettore dalle cose della cui verità è già certo a una nuova conoscenza che non appare necessariamente evidente non appena guardiamo un cerchio. Il trucco sta nel tracciare una terza linea che va dal punto iniziale sul cerchio, B, al centro del cerchio in O.

Perché questa terza linea ci è d’aiuto? Perché ora abbiamo due triangoli con due lati di eguale lunghezza. Ciò significa che, in entrambi i triangoli, i due angoli opposti al centro del cerchio sono congruenti; questa proprietà è già stata dimostrata per tali triangoli. Prendiamo in considerazione il più grande, quello che abbiamo disegnato all’inizio: i suoi angoli corrispondono alla somma 2α + 2β. Combiniamo quindi questo risultato con la conoscenza del fatto che in un triangolo la somma degli angoli interni è pari a 180 gradi, e potremo concludere che la somma α + β deve misurare 90 gradi, come asserito da Talete.

Da bambino, quando ho visto per la prima volta questa dimostrazione, mi sono davvero entusiasmato. Potevo cogliere già dai disegni che l’angolo sulla circonferenza sembrava un angolo retto, ma come facevo a esserne certo? La mia mente cercava una ragione per cui le cose dovevano stare necessariamente così. Quindi, ho voltato pagina e ho visto la terza linea tracciata da Talete fino al centro del cerchio, e ho intuito le implicazioni logiche che ne seguivano. All’improvviso, ho capito con assoluta chiarezza perché quell’angolo doveva misurare 90 gradi.

Va notato che già in questa dimostrazione potete vedere come l’edificio matematico viene costruito sopra cose già dimostrate, cose come il fatto che la somma degli angoli interni di un triangolo è pari a 180 gradi. E la scoperta di Talete, a sua volta, diventa un nuovo mattone con cui costruire lo strato successivo.

La dimostrazione di Talete è una delle tante che compaiono negli Elementi di Euclide, il libro che molti considerano il modello di riferimento per la matematica e la dimostrazione. Parte da alcuni elementi costitutivi fondamentali, gli assiomi, asserzioni di geometria che sembrano così palesemente evidenti da poter essere accettate come le fondamenta sicure su cui iniziare a costruire gli argomenti logici.

L’idea di dimostrazione non emerse dal nulla come il frutto dell’ingegno di un singolo individuo isolato, ma comparve insieme a un nuovo stile di scrittura sviluppatosi nell’antica Grecia. L’arte della retorica, formulata da filosofi come Aristotele, rappresentava una nuova forma di discorso mirato a convincere il pubblico: che si trattasse di una disputa legale, di un confronto politico o, semplicemente, della narrazione di una storia, il pubblico veniva condotto in un viaggio logico in cui l’oratore tentava di convincerlo delle proprie posizioni. La matematica egiziana e babilonese era nata dalle esigenze legate alla costruzione e alla misurazione delle nuove città che crescevano attorno all’Eufrate e al Nilo; questo nuovo bisogno di argomenti logici e retorici, invece, nacque dalle istituzioni politiche delle fiorenti città-Stato al cuore dell’impero greco.

Per Aristotele, la retorica consisteva in una combinazione di pura logica e metodi pensati per far leva sulle emozioni del pubblico. La dimostrazione matematica attinge al primo di questi due elementi, ma ha anche a che fare con la narrazione delle storie; ed è questo il motivo per cui lo sviluppo della dimostrazione in questa precisa epoca e in questo preciso posto fu probabilmente legato tanto alle sofisticate narrazioni costruite dai drammaturghi come Sofocle ed Euripide quanto ai dialoghi filosofici di Aristotele e Platone.

A loro volta, le esplorazioni matematiche dei greci si spinsero oltre gli algoritmi finalizzati alla costruzione degli edifici e ai rilevamenti topografici per procedere verso sorprendenti scoperte che assomigliavano a storie matematiche per eccitare un lettore.

Una dimostrazione è una narrazione logica che accompagna il lettore da un posto che gli è noto a una nuova destinazione dove non è mai stato prima. Come le avventure di Frodo nel Signore degli anelli di Tolkien, una dimostrazione è una descrizione del viaggio dalla Contea a Mordor. All’interno dei familiari confini della Contea ci sono gli assiomi della matematica, le verità di per sé evidenti sui numeri, insieme alle proposizioni già dimostrate. È da qui che parte la ricerca. Il viaggio da questo territorio deve obbedire alle regole della deduzione matematica – come le mosse legittime di un pezzo degli scacchi – che stabiliscono i passi che possiamo fare attraverso questo mondo. A volte capita di arrivare a quello che sembra un vicolo cieco, e occorre fare un passo laterale o magari anche tornare indietro per cercare un modo per aggirare l’ostacolo. Talvolta, per poter continuare il viaggio bisogna aspettare la creazione di nuovi personaggi matematici, come i numeri immaginari o il calcolo infinitesimale. La dimostrazione è la storia del viaggio e la mappa che ne segna le coordinate. Il registro di bordo del matematico.

Per guadagnarsi un posto nel canone matematico, al viaggio non basta produrre un’affermazione vera sui numeri o la geometria: deve sorprendere, deliziare, toccare il lettore. Dovrebbe contenere drammi e pericoli. La matematica non è una semplice raccolta di affermazioni vere sui numeri, così come la letteratura non è l’insieme di tutte le possibili combinazioni di parole e la musica di tutte le possibili combinazioni di note. La matematica richiede giudizio estetico e scelta, ed è probabile che sia proprio questo il motivo per cui l’arte della dimostrazione matematica è nata in un periodo in cui la narrazione delle storie era un’attività fiorente. La dimostrazione non è in debito solo con il logos della retorica di Aristotele, ma anche – e, probabilmente, in egual misura – con il suo pathos.

Numeri oltre i confini

Per quanto molte delle prime dimostrazioni geometriche siano costruttive, gli antichi greci usarono i loro nuovi strumenti matematici anche per dimostrare che determinate cose sono impossibili, assurde. Un esempio, come abbiamo già visto, è dato dalla scoperta che la radice quadrata di 2 non può essere scritta sotto forma di frazione.

Anche questa dimostrazione ha un carattere molto narrativo: il lettore viene accompagnato in un viaggio fatto sulla base dell’assunzione che la lunghezza della diagonale di un quadrato unitario pos...

Indice dei contenuti

• Copertina
• Frontespizio
• Dedica
• Confine zero: le incognite note
• PRIMO CONFINE: IL DADO DA CASINÒ
• SECONDO CONFINE: IL VIOLONCELLO
• TERZO CONFINE: IL BARATTOLO DELL’URANIO
• QUARTO CONFINE: L’UNIVERSO RITAGLIATO
• QUINTO CONFINE: L’OROLOGIO DA POLSO
• SESTO CONFINE: IL CHATTERBOT
• SETTIMO CONFINE: IL CRACKER NATALIZIO
• Ringraziamenti
• Note
• Crediti delle illustrazioni
• Altre letture
• Indice dei nomi e dei luoghi
• Indice