Contro l'ora di matematica

Un manifesto per la liberazione di professori e studenti

Paul Lockhart

• Editore: RIZZOLI
• Anno: 2010
• Print ISBN: 9788817038409
• eBook ISBN: 9788858602188

REGOLA N° 1 L'equazione (MATEMATICA = NOIA + FATICA) è sbagliata. REGOLA N° 2 Non esiste nulla di più idealistico e poetico, nulla di più radicale, sovversivo e psichedelico della matematica. Formule da memorizzare, procedure da seguire, definizionida ripetere parola per parola, simboli astrusi da manipolare: è questa la matematica? No, è solo la triste caricatura cuil'ha ridotta la scuola. A dirlo è un professore che ha decisodi rivoluzionare i metodi di insegnamento ansiogeni, terroristici, frustranti che il programma gli imporrebbe. Perchéla vera matematica è una sublime forma d'arte, è la creazionee l'esplorazione di un mondo immaginario abitato da creature fantastiche, è "poesia della ragione". Questo piccololibro ricolmo di passione è insieme una critica impietosaa un'istruzione che uccide ogni piacere della scoperta e uninno gioioso alla libera attività dello spirito.

REGOLA N° 1

L’equazione (MATEMATICA = NOIA + FATICA) è sbagliata.

REGOLA N° 2

Non esiste nulla di più idealistico e poetico, nulla di più radicale, sovversivo e psichedelico della matematica.

Formule da memorizzare, procedure da seguire, definizionida ripetere parola per parola, simboli astrusi da manipolare:è questa la matematica? No, è solo la triste caricatura cuil’ha ridotta la scuola. A dirlo è un professore che ha decisodi rivoluzionare i metodi di insegnamento ansiogeni, terroristici, frustranti che il programma gli imporrebbe. Perchéla vera matematica è una sublime forma d’arte, è la creazionee l’esplorazione di un mondo immaginario abitato da creature fantastiche, è “poesia della ragione”. Questo piccololibro ricolmo di passione è insieme una critica impietosaa un’istruzione che uccide ogni piacere della scoperta e uninno gioioso alla libera attività dello spirito.

Prefazione

Verso la fine del 2007, una persona che assisteva a una mia conferenza mi consegnò un dattiloscritto di venticinque pagine intitolato A Mathematician’s Lament. Pensava, mi disse, che mi sarebbe potuto piacere. Firmato da un insegnante di matematica di nome Paul Lockhart, quel saggio circolava in maniera piuttosto discontinua nella comunità scolastica fin da quando l’autore l’aveva scritto, nel 2002, ma non era mai stato pubblicato. La previsione di quello spettatore della mia conferenza si rivelò sbagliata per difetto: mi innamorai del saggio, e pensai che le parole di quel Paul Lockhart, chiunque fosse, meritassero un pubblico molto più vasto. Così feci qualcosa che non avevo mai fatto prima e che probabilmente non farò mai più: dopo aver rintracciato l’autore – non senza qualche difficoltà, dato che il dattiloscritto non conteneva informazioni per contattarlo – e dopo aver ottenuto il suo permesso, dedicai l’intero spazio di Devlin’s Angle, la rubrica mensile che tengo per «MAA Online», il magazine online della Mathematical Association of America, alla riproduzione del saggio nella sua forma originale. Era il modo più veloce ed efficace che conoscessi per sottoporlo all’attenzione delle comunità dei matematici e degli insegnanti di matematica.

Quando A Mathematician’s Lament apparve nella mia rubrica, nel marzo del 2008, lo presentai con queste parole:

Si tratta, in tutta franchezza, di una delle migliori critiche all’attuale insegnamento della matematica nella scuola dell’obbligo che io abbia mai visto.

Mi aspettavo una reazione forte. Ciò che seguì fu un uragano. Le parole di Paul toccavano un tasto estremamente sensibile, che risuonò in tutto il mondo. Oltre a molte e-mail che esprimevano apprezzamento, giunse una marea di richieste – molte indirizzate a me, dato che in base agli accordi presi con Paul non avevo fornito i suoi recapiti – per i diritti di riproduzione e di traduzione. (Il volume che avete in mano è nato esattamente in questo modo.)

Non che Paul dicesse qualcosa di diverso da ciò che innumerevoli matematici e insegnanti di matematica avevano detto prima di lui. E nemmeno le questioni che sollevava erano nuove per coloro che, nel mondo talvolta spaccato della didattica della matematica, scrivevano di dissentire su molto se non su tutto ciò che egli affermava. Di diverso c’erano l’eloquenza delle sue parole e l’evidente passione che vi trasfondeva. Non era semplicemente buona scrittura; quella era grande scrittura che colpiva dritta al cuore.

A scanso d’equivoci, sappiate che A Mathematician’s Lament, così come questa sua versione in volume decisamente ampliata, è uno scritto d’opinione. Paul ha idee molto forti riguardo a come andrebbe insegnata la matematica; sostiene con energia la sua posizione e con altrettanta energia si oppone a buona parte dello status quo nella didattica scolastica. Ciò che lo rende unico, oltre al suo stile di scrittura personale e accattivante, è il fatto che sulle questioni spinose e molto dibattute relative alla matematica insegnata a scuola egli introduce una prospettiva che pochi altri sono in grado di adottare. Paul è uno di quei rari casi di persone che hanno cominciato la loro carriera come ricercatori matematici di professione, insegnando la materia agli studenti universitari, per poi rendersi conto che la loro vera vocazione era l’insegnamento per la scuola dell’obbligo, ovvero la professione che egli esercita ormai da molti anni.

Secondo me questo libro, così come il saggio da cui trae origine, dovrebbe costituire una lettura obbligatoria per chiunque si occupi professionalmente di insegnare la matematica, per ogni genitore che abbia un figlio in età scolare e per ogni funzionario scolastico o governativo che abbia delle responsabilità relative all’insegnamento della matematica. Forse non vi troverete d’accordo con tutto quello che Paul sostiene, forse riterrete che il suo approccio all’insegnamento non possa essere adottato con successo da ogni insegnante, ma le sue parole saranno senz’altro un ottimo spunto di riflessione. Questo breve saggio è riconosciuto come una pietra miliare dalla comunità degli insegnanti di matematica, una lettura imprescindibile. Non vi anticiperò la reazione che immagino avrete nel leggere questo saggio; è giusto che ognuno di voi lo scopra strada facendo, e sono sicuro che Paul sarebbe pienamente d’accordo. Una cosa però posso confidarvela: avrei tanto desiderato avere Paul Lockhart come insegnante di matematica!

Keith Devlin,

Stanford University

CONTRO l’ORA
di MATEMATICA

Se vuoi costruire una nave, non radunare uomini per raccogliere il legno, distribuire i compiti e suddividere il lavoro, ma insegna alla gente la nostalgia del mare infinito.

Antoine de Saint-Exupéry

Parte I

Lamentazione

Matematica e cultura

La prima cosa da chiarire è che la matematica è un’arte. La differenza tra la matematica e le altre arti, come la musica e la pittura, è che la nostra cultura non la riconosce come tale. Tutti comprendono che i poeti, i pittori e i musicisti creano delle opere d’arte e che si esprimono per mezzo di parole, immagini e suoni. In effetti la nostra società è piuttosto generosa nei riguardi delle manifestazioni di creatività: architetti, chef e persino registi televisivi sono considerati artisti. Perché, allora, non i matematici?

In parte il problema è dato dal fatto che nessuno ha la minima idea di quello che i matematici fanno. A quanto pare, l’impressione comune è che i matematici siano legati in qualche modo alla scienza: forse aiutano gli scienziati con le loro formule, o inseriscono grandi numeri nei computer per una ragione o per l’altra. Certo è che, se dovessimo dividere il mondo in «sognatori poetici» e «pensatori razionali», la maggioranza delle persone porrebbe i matematici nella seconda categoria.

Ma la verità è che non esiste nulla di più poetico e visionario, nulla di più radicale, sovversivo e psichedelico della matematica. La matematica non è meno stupefacente della cosmologia o della fisica (i matematici hanno concepito i buchi neri ben prima che gli astronomi ne scoprissero uno) e offre una maggiore libertà espressiva rispetto alla poesia, all’arte o alla musica (che dipendono fortemente dalle proprietà dell’universo fisico). La matematica è la più pura delle arti, e la più fraintesa.

Permettetemi dunque di tentare di spiegarvi cos’è davvero la matematica e cosa fanno i matematici. Il modo migliore per cominciare è citare l’eccellente descrizione che ne dà G. H. Hardy:

Il matematico, come il pittore e il poeta, è un creatore di forme. Se le forme che crea sono più durature delle loro, è perché sono fatte di idee.^*

Dunque i matematici passano il tempo creando forme fatte di idee. Che genere di idee? Idee sui rinoceronti? No, quelle le lasciamo ai biologi. Idee sul linguaggio e la cultura? No, almeno non di solito. Cose di questo genere sono decisamente troppo complicate per il gusto della maggior parte dei matematici. Se mai esiste un principio estetico unificante in matematica, è questo: semplice è bello. Ai matematici piace pensare alle cose più semplici possibili, e le cose più semplici possibili sono immaginarie.

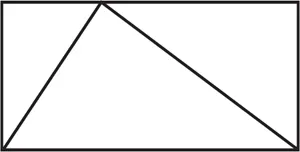
Per esempio, se ho voglia di pensare a delle figure geometriche – e mi capita spesso – potrei immaginare un triangolo all’interno di un riquadro rettangolare:

Mi chiedo quanta parte del rettangolo occupi il triangolo; due terzi, forse? Quel che è importante comprendere è che non sto parlando di questo particolare disegno di un triangolo dentro un rettangolo. Né sto parlando di un triangolo di metallo che fa parte del sistema di travi di un ponte. Non c’è alcun fine recondito di tipo pratico in ciò che immagino. Sto semplicemente giocando. La matematica non è che questo: porsi domande, giocare, trastullarsi con la propria immaginazione. Tanto per cominciare, chiedersi quanta parte del rettangolo occupi il triangolo non ha nemmeno senso per degli oggetti fisici, reali. Anche il triangolo materiale realizzato con il massimo della cura rimane sempre un insieme irrimediabilmente complicato di atomi che si agitano, cambiando continuamente forma. A meno che non si voglia parlare di misurazioni approssimate di un qualche tipo. Ed è proprio qui che interviene l’estetica, perché quel problema non è semplice, anzi, è un problema complesso che dipende da una serie di variabili e dettagli connessi con il mondo reale. Lasciamolo agli scienziati. Il problema matematico riguarda invece un triangolo immaginario all’interno di un rettangolo immaginario. I bordi sono perfetti perché io voglio che lo siano; ed è questo il tipo di oggetti ai quali preferisco pensare. È un tema importante, in matematica: le cose sono ciò che desideriamo siano. Le scelte a nostra disposizione sono infinite, non esiste alcuna realtà a intralciarci.

D’altra parte, una volta che abbiamo compiuto le nostre scelte (per esempio, io potrei decidere di creare il mio triangolo simmetrico oppure no), allora le nostre nuove creazioni fanno quello che devono, che ci piaccia o no. È questo l’aspetto sorprendente della creazione di forme immaginarie: rispondono perfettamente! Il triangolo occupa una certa porzione del rettangolo in cui è inscritto, e io non ho alcun controllo sull’entità di quella porzione! C’è un numero che collega le due forme: forse è due terzi, forse no, non so ancora quale sia. Devo scoprirlo.

Perciò possiamo giocare e immaginare tutto ciò che vogliamo, creare forme e porci domande su di esse. Ma come rispondiamo a queste domande? Non certo come fa la scienza. Non esistono esperimenti da compiere con provette e strumenti, o con qualcosa che dirà la verità su una creazione dell’immaginazione. L’unico modo per raggiungere la verità sulla nostra immaginazione è usare la nostra immaginazione, ed è faticoso.

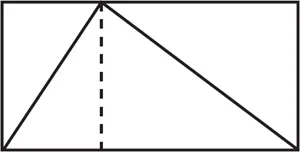
Nel caso del triangolo dentro il suo rettangolo, riesco a vedere qualcosa di semplice e bello:

Se divido il rettangolo in due parti in questo modo, mi rendo conto che ciascuna di esse risulta tagliata diagonalmente a metà da uno dei lati del triangolo. Dunque lo spazio che sta all’interno del triangolo è uguale a quello che sta al suo esterno. Ciò significa che il triangolo deve occupare esattamente metà del rettangolo!

Ecco com’è fare matematica. Questo è solo un piccolo esempio di ciò in cui consiste l’arte del matematico: porsi domande semplici ed eleganti su creazioni immaginarie ed elaborare spiegazioni soddisfacenti e belle. Non esiste nulla che assomigli lontanamente a questo regno delle idee pure: è affascinante, è divertente ed è libero!

Ma da dove mi è venuta quell’idea? Come facevo a sapere di dover tracciare quella linea? Come fa un pittore a sapere dove appoggiare il suo pennello? Ispirazione, esperienza, tentativi ed errori, mera fortuna. Sta in questo, l’arte della matematica: nel creare queste piccole, stupende poesie del pensiero, questi sonetti di pura ragione. È una forma d’arte che possiede una meravigliosa capacità di trasformazione. Il rapporto fra il triangolo e il rettangolo era un mistero, e poi quell’unica linea l’ha reso palese. Non riuscivo a scorgere quel rapporto; poi, d’un tratto, ho potuto vederlo. In qualche modo, sono stato in grado di creare qualcosa di bello e profondo dal nulla e, nel farlo, di cambiare me stesso. Non è in questo che consiste l’arte?

Ecco perché è così sconfortante vedere ciò che si sta facendo della matematica a scuola. Questa ricca e affascinante avventura dell’immaginazione è stata ridotta a una sterile sequela di dati da memorizzare e di procedure da seguire. Invece di una domanda semplice e naturale su alcune figure, invece di un processo creativo e gratificante di invenzione e di scoperta, agli studenti viene offerto questo:

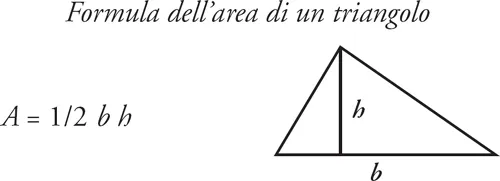
«L’area di un triangolo è uguale alla base per l’altezza diviso due.» Agli studenti è richiesto di imparare a memoria questa formula per poi «applicarla» di continuo negli «esercizi». Addio all’eccitazione, alla gioia, persino al dolore e alla frustrazione dell’atto creativo! Non rimane nemmeno più un problema da risolvere. La domanda è stata formulata e nello stesso tempo è stata fornita la risposta: allo studente non rimane niente da fare.

Desidero però essere chiaro riguardo a ciò che disapprovo. Non sono contrario né alle formule né alla memorizzazione di fatti interessanti. Questo va bene all’interno di un dato contesto, e ha una sua funzione così come ha una sua funzione l’apprendimento del vocabola...

Indice dei contenuti

• Cover
• Frontespizio
• Contro l’ora di Matematica. Un manifesto per la liberazione di professori e studenti
• Indice