Qualcosa di nascosto a fondo

Il mondo dei quanti e l'emergere dello spaziotempo

Sean Carroll, Daniele A. Gewurz

• Editore: EINAUDI
• Anno: 2020
• Print ISBN: 9788806245771
• eBook ISBN: 9788858434697
• Argomento: Scienze fisiche
• Categoria: Fisica

Con questo libro, Sean Carroll, fisico teorico e tra gli scrittori di scienza piú famosi al mondo, riscrive la storia della fisica del XX secolo. Acclamato come un capolavoro, Qualcosa di nascosto a fondo per la prima volta dimostra che affrontare il principale enigma della meccanica quantistica significa trasformare completamente il modo in cui pensiamo allo spazio e al tempo. Carroll riconcilia la meccanica quantistica con la teoria della relatività di Einstein, e questo cambia davvero tutto. La maggior parte dei fisici non ha mai ammesso la spiacevole verità: la fisica è in crisi dal 1927. La meccanica quantistica ha sempre mostrato lacune evidenti, che semplicemente si è preferito ignorare. I divulgatori sottolineano quanto vi sia di misterioso e impossibile da capire. I professori scoraggiano gli studenti dall'inoltrarsi nel «vicolo cieco» delle basi della teoria quantistica. Carroll invece, con questo libro audace quanto plausibile, afferma che la crisi può trovare una sua fine. Dobbiamo solo accettare che ci sia piú di uno di noi nell'universo. Ci sono molti e molti Sean Carroll. Molti di ognuno di noi. Copie di ognuno di noi vengono generate migliaia di volte al secondo. In accordo con la teoria dei comportamenti quantistici dei molti mondi, ogni volta che si verifica un evento quantistico, un mondo si divide insieme a tutto ciò che contiene, a eccezione di quell'altro mondo in cui l'evento non si è verificato. Passo dopo passo e con estrema lucidità, Carroll affronta le principali obiezioni a questa sorta di rivelazione ultraterrena, fino a quando la sua tesi non risulterà inesorabilmente dimostrata. Raramente un libro ha riorganizzato cosí a fondo i termini in cui pensiamo al nostro posto nell'universo. Siamo sulla soglia di una nuova comprensione del luogo in cui ci troviamo nel cosmo e di cosa siamo fatti. «La meccanica quantistica non merita la definizione di "inquietante", nel senso di un qualche mistero ineffabile al di là della comprensione umana. La meccanica quantistica è sorprendente; è una visione della realtà nuova, profonda, sbalorditiva e molto diversa da quella a cui siamo abituati. La scienza è cosí, a volte. Ma se un argomento sembra difficile o sconcertante, la risposta scientifica è risolvere l'enigma, non fare finta che non ci sia».«Un emozionante tour attraverso quello che è forse il piú grande successo intellettuale dell'umanità: la meccanica quantistica. Con audace chiarezza, Carroll smaschera abilmente la stranezza quantistica per rivelare una realtà inusuale ma assolutamente meravigliosa».
Brian Greene «Sean Carroll chiarisce magnificamente il dibattito sui fondamenti della meccanica quantistica, difendendo l'approccio piú elegante e coraggioso: la sorprendente interpretazione di "molti mondi". Le sue spiegazioni dei pro e dei contro sono chiare, obiettive e filosoficamente sbalorditive».
Steven Strogatz «Irresistibile, un assoluto piacere per il lettore. Non solo un libro su alcuni dei piú profondi e attuali misteri della fisica, ma anche un libro sulla metafisica: con lucidità Carroll ci mostra come pensare non solo alla natura vera e nascosta della realtà, ma anche come darle un senso. Ho adorato questo libro».
Priyamvada Natarajan

Parte seconda

Divisione

Capitolo sesto

Dividere l’universo

Decoerenza e mondi paralleli

L’articolo di Einstein-Podolsky-Rosen del 1935 sull’entanglement quantistico e la risposta di Niels Bohr furono gli ultimi importanti scambi pubblici nel dibattito tra Bohr e Einstein sui fondamenti della meccanica quantistica. I due fisici avevano avuto un carteggio sulla teoria quantistica da quando nel 1913 Bohr aveva proposto il modello delle orbite quantizzate degli elettroni, ma la loro disputa aveva raggiunto l’apice in occasione del Congresso Solvay del 1927. Nella vulgata popolare Einstein avrebbe sollevato delle obiezioni sull’interpretazione di Copenaghen, attorno a cui si radunavano i consensi, in occasione del Congresso durante le conversazioni con Bohr, che avrebbe trascorso una serata pensieroso per poi, l’indomani a colazione, presentare trionfalmente la sua controreplica a Einstein, rimettendolo al suo posto. Ci viene detto che Einstein semplicemente non si capacitava della validità del principio di indeterminazione e dell’idea che Dio giochi a dadi con l’universo.

Non è propriamente cosí che andò. Le preoccupazioni primarie di Einstein non riguardavano la casualità ma il realismo e la località. Il suo atteggiamento improntato alla salvaguardia di questi principî culminò nell’articolo EPR e nell’argomentazione secondo cui la meccanica quantistica è incompleta. Ma a quel punto la battaglia delle pubbliche relazioni era persa e l’approccio di Copenaghen alla meccanica quantistica era stato adottato dai fisici di tutto il mondo, che si erano messi ad applicarla ai problemi tecnici della fisica atomica e nucleare, nonché ai campi emergenti della fisica delle particelle e della teoria quantistica dei campi. Le implicazioni dell’articolo furono in buona misura ignorate dalla comunità. Affannarsi sugli aspetti confusi alla base della teoria quantistica anziché lavorare su problemi fisici piú tangibili cominciò a sembrare un’impresa un po’ eccentrica, che poteva occupare il tempo di fisici non piú produttivi, una volta che avevano raggiunto una certa età ed erano pronti ad abbandonare il vero lavoro.

Nel 1933 Einstein lasciò la Germania e cominciò a lavorare presso il nuovo Institute for Advanced Study a Princeton, nel New Jersey, dove sarebbe rimasto fino alla morte nel 1955. Dopo il 1935 il suo lavoro tecnico si concentrò in gran parte sulla relatività generale classica e sulla ricerca di una teoria unificata della gravitazione e dell’elettromagnetismo, ma non smise mai di pensare alla meccanica quantistica. Occasionalmente Bohr visitava Princeton, dove proseguiva il dialogo con Einstein.

Nel 1934 John Archibald Wheeler entrò a far parte della facoltà di fisica dell’Università di Princeton come assistant professor. Piú avanti Wheeler sarebbe diventato noto come uno dei massimi esperti al mondo di relatività generale e avrebbe reso popolari i termini «buco nero» e «wormhole», ma all’inizio della carriera si occupò di problemi quantistici. Aveva studiato brevemente con Bohr a Copenaghen e nel 1939 aveva pubblicato insieme al danese uno dei primi articoli sulla fissione nucleare. Wheeler nutriva una grande ammirazione per Einstein, ma venerava Bohr; come avrebbe affermato in seguito: «Nulla ha contribuito di piú a convincermi che in passato esistettero amici dell’umanità con la saggezza umana di Confucio e Buddha, Gesú e Pericle, Erasmo e Lincoln, quanto le passeggiate e le conversazioni con Niels Bohr sotto i faggi della foresta di Klampenborg»¹.

Wheeler è stato importante per la fisica in diversi modi, uno dei quali fu l’aver seguito alcuni dottorandi di talento, tra cui futuri premi Nobel come Richard Feynman e Kip Thorne. Uno di questi studenti fu Hugh Everett III, che avrebbe introdotto un approccio significativamente nuovo al modo di pensare alla base della meccanica quantistica. Abbiamo già accennato alla sua idea fondamentale – la funzione d’onda rappresenta la realtà, si evolve in modo continuo e quando si effettua una misurazione quantistica questa evoluzione porta a mondi multipli distinti –, ma ora abbiamo gli strumenti per farlo adeguatamente.

La proposta di Everett, che avrebbe costituito la sua tesi di dottorato del 1957 a Princeton, si può considerare come l’incarnazione piú pura di uno dei principî preferiti di Wheeler: che la fisica teorica debba essere «radicalmente conservatrice». L’idea consiste nel fatto che una buona teoria fisica debba essere stata messa alla prova sulla base di dati sperimentali, ma solo in regimi che gli sperimentatori sono effettivamente in grado di raggiungere. Bisogna essere conservatori nel senso che dobbiamo partire dalle teorie e dai principî che sono già stati stabiliti come efficaci, piuttosto che introdurre arbitrariamente nuovi approcci ogni volta che si incontrano nuovi fenomeni. Ma bisogna anche essere radicali, nel senso che le previsioni e le conseguenze delle nostre teorie devono essere prese sul serio pure in regimi ben al di là di quelli in cui sono state testate. Le espressioni «dobbiamo partire» e «devono essere prese sul serio» sono essenziali; è ovvio che servono nuove teorie quando si osserva che quelle vecchie contraddicono palesemente i nuovi dati, e solo perché una previsione viene presa sul serio non significa che non vada rivista alla luce di nuove informazioni. Ma la filosofia di Wheeler consiste nell’iniziare in modo prudente, da aspetti della natura che riteniamo di comprendere, e poi nell’agire in modo coraggioso, estrapolando le nostre migliori idee fino ai confini dell’universo.

Parte dell’ispirazione di Everett era la ricerca di una teoria della gravità quantistica, alla quale Wheeler si era recentemente interessato. Il resto della fisica – materia, elettromagnetismo, forze nucleari – sembra rientrare senza problemi nell’ambito della meccanica quantistica. Ma la gravità era (e rimane) un’ostinata eccezione. Nel 1915 Einstein propose la teoria della relatività generale, secondo la quale lo spaziotempo stesso è un’entità dinamica la cui forma e curvatura sono ciò che noi percepiamo come forza di gravità. La relatività generale è però una teoria completamente classica, con analoghi della posizione e della quantità di moto per la curvatura dello spaziotempo e senza limitazioni sul modo in cui misurarli. Prendere questa teoria e «quantizzarla», costruire una teoria delle funzioni d’onda dello spaziotempo anziché specifici spazitempi classici si è rivelato difficile.

Hugh Everett III (Per gentile concessione dello Hugh Everett III Archive presso l’Università della California a Irvine e di Mark Everett).

Le difficoltà della gravità quantistica sono sia tecniche – i calcoli tendono a esplodere e a dare risposte infinitamente grandi – sia concettuali. Persino nella meccanica quantistica, malgrado si possa non essere in grado di dire dove si trovi esattamente una certa particella, la nozione di «un punto dello spazio» è perfettamente ben definita. Possiamo specificare una posizione e chiedere qual è la probabilità di trovare la particella lí vicino. Ma se la realtà non è costituita da cose distribuite nello spazio, bensí è una funzione d’onda quantistica che descrive le sovrapposizioni di diversi spazitempi possibili, come possiamo anche solo chiedere «dove» si osserva una determinata particella?

Le difficoltà aumentano ancor piú quando passiamo al problema della misura. Negli anni Cinquanta la scuola di Copenaghen era la dottrina attestata e i fisici avevano fatto pace con l’idea che le funzioni d’onda collassino quando si svolge una misurazione. Erano persino disposti a trattare il processo di misurazione come una parte fondamentale del modo migliore che conosciamo per descrivere la natura. O, perlomeno, a non preoccuparsene troppo.

Ma che cosa succede quando il sistema quantistico in esame è l’intero universo? Per l’approccio di Copenaghen era essenziale la distinzione tra il sistema quantistico che si sta misurando e l’osservatore classico che svolge la misurazione. Se il sistema è l’universo nel suo complesso, ci siamo dentro tutti e non esiste un osservatore esterno a cui possiamo appellarci. Anni dopo, Stephen Hawking e altri avrebbero affrontato la cosmologia quantistica per studiare come un universo compiuto possa avere un primo momento nel tempo, presumibilmente identificato con il Big Bang.

Mentre Wheeler e altri pensavano alle difficoltà tecniche della gravità quantistica, Everett rimase affascinato da questi problemi concettuali, in particolare da come gestire le misurazioni. Le origini della formulazione dei molti mondi si possono rintracciare in una discussione a tarda sera avvenuta nel 1954 con i giovani colleghi fisici Charles Misner (un altro studente di Wheeler) e Aage Petersen (un assistente di Bohr, in visita da Copenaghen). Tutti i presenti avrebbero concordato sul fatto che in quell’occasione si consumarono fiumi di Sherry.

Chiaramente, ragionava Everett, se intendiamo parlare dell’universo in termini quantistici, non possiamo ritagliarci un ambito classico separato. Ogni parte dell’universo dovrà essere trattata secondo le regole della meccanica quantistica, compresi gli osservatori al suo interno. Ci sarà un solo stato quantistico, descritto da quella che Everett chiamava «funzione d’onda universale» (e che noi abbiamo chiamato «la funzione d’onda dell’universo»).

Se tutto è quantistico e l’universo è descritto da una singola funzione d’onda, in che cosa dovrebbe consistere la misurazione? Si verifica, ragionò Everett, quando una parte dell’universo interagisce con un’altra parte dell’universo in un modo opportuno. È un evento che accadrà automaticamente, osservò, semplicemente per via dell’evoluzione della funzione d’onda universale secondo l’equazione di Schrödinger. Non è necessario invocare alcuna regola speciale per le misurazioni; le cose interagiscono tra loro in continuazione.

È per questo motivo che Everett intitolò il suo articolo sull’argomento «Relative State» Formulation of Quantum Mechanics (Formulazione della meccanica quantistica in termini di «stati relativi»). Quando uno strumento di misura interagisce con un sistema quantistico, i due entrano in entanglement. Non ci sono collassi della funzione d’onda o ambiti classici; è l’apparato stesso a evolversi in una sovrapposizione, entangled con lo stato della cosa osservata. Il risultato della misura, apparentemente ben definito («l’elettrone ha lo spin su»), è relativo solo a un particolare stato dello strumento («ho misurato l’elettrone con lo spin su»). Gli altri possibili risultati della misurazione continuano a esistere e sono perfettamente reali, a parte il fatto che si trovano in mondi distinti. Non dobbiamo fare altro che affrontare coraggiosamente ciò che la meccanica quantistica cerca da sempre di dirci.

Cerchiamo di essere un po’ piú espliciti su che cosa accade quando viene effettuata una misurazione, secondo la teoria di Everett.

Immaginiamo di avere un elettrone dotato di spin, che si può osservare con spin su o spin giú, rispetto all’asse scelto. Prima della misurazione, l’elettrone si trova in genere in una sovrapposizione di su e giú. Abbiamo anche uno strumento di misura, che è a sua volta un sistema quantistico. Immaginiamo che possa trovarsi in una sovrapposizione di tre diverse possibilità: può aver misurato uno spin su, può aver misurato uno spin giú, o può non aver ancora misurato lo spin, stato che chiamiamo «pronto».

Il fatto che l’apparato di misurazione funziona ci dice come si evolve lo stato quantistico del sistema combinato spin + apparato secondo l’equazione di Schrödinger. In particolare, se iniziamo con l’apparato nello stato pronto e con lo spin in uno stato puramente spin su, ci è garantito che l’apparato si evolve in uno stato puro corrispondente alla misurazione dello spin su, cosí:

Lo stato iniziale a sinistra si può leggere come «lo spin è nello stato su e l’apparato è nello stato pronto», mentre quello a destra, in cui la lancetta indica la freccia verso l’alto, come «lo spin è nello stato su e l’apparato ha misurato che è su».

Allo stesso modo, la capacità di misurare con successo uno stato puro di spin giú indica che l’apparato deve evolversi da «pronto» a «misurato giú»:

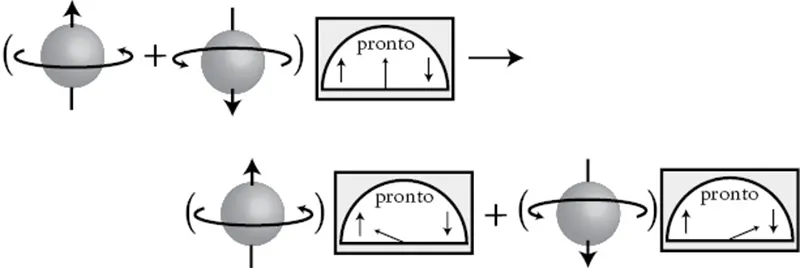
Ciò che ci interessa, ovviamente, è capire che cosa succede quando lo spin iniziale non è uno stato puro su o giú, ma in qualche sovrapposizione dei due. La bella notizia è che sappiamo già tutto ciò che ci serve. Le regole della meccanica quantistica sono chiare: se sappiamo come si evolverà un sistema a partire da due stati diversi, l’evoluzione di una sovrapposizione di questi due stati sarà semplicemente una sovrapposizione delle due evoluzioni. In altre parole, partendo da uno spin in una certa sovrapposizione e dal dispositivo di misurazione nello stato pronto, abbiamo:

Lo stato finale ora è una sovrapposizione in entanglement: lo spin è su ed è stato misurato su piú lo spin è giú ed è stato misurato giú. A questo punto non è strettamente corretto dire «lo spin è in sovrapposizione» o «l’apparato è in sovrapposizione». L’entanglement ci impedisce di parlare separatamente della funzione d’onda dello spin o di quella dell’apparato, perché quello che osserveremo di uno può dipendere da quello che osserviamo dell’altro. L’unica cosa che possiamo dire è: «il sistema spin + apparato è in sovrapposizione».

Questo stato finale è la funzione d’onda finale nitida, inequivocabile e definitiva per il sistema combinato spin + apparato, se non facciamo altro che farla evolvere secondo l’equazione di Schrödinger. È questo il segreto della meccanica quantistica di Everett. L’equazione di Schrödinger afferma che un accurato strumento di misurazione si evolverà in una sovrapposizione macroscopica, che interpreteremo in definitiva come ramificazione in mondi separati. Non abbiamo inserito noi i mondi; ci sono sempre stati e l’equazione di Schrödinger li porta inevitabilmente in vita. Il problema è che nella nostra esperienza del mondo non sembra che ci imbattiamo mai in sovrapposizioni che coinvolgono grandi oggetti macroscopici.

Il rimedio tradizionale è stato di manipolare in qualche modo le regole fondamentali della meccanica quantistica. Alcuni approcci affermano che l’equazione di Schrödinger non è sempre applicabile, altri che ci sono ulteriori variabili al di là della funzione d’onda. L’approccio di Copenaghen parte dal non trattare l’apparato di misura come un sistema quantistico e dal considerare il collasso della funzione d’onda come una maniera a sé stante in cui può evolversi lo stato quantistico. In un modo o nell’altro ognuno di questi approcci invoca qualche tortuosità per non accettare, quale descrizione vera e completa della natura, sovrapposizioni pari a quella mostrata sopra. Come dirà Everett in seguito: «L’interpretazione di Copenaghen è irrimediabilmente incompleta a causa della sua dipendenza a priori dalla fisica classica [ed è] una mostruosità filosofica che ha un concetto di “realtà” per il mondo macroscopico e lo nega per il microcosmo»².

La ricetta di Everett era semplice: smettiamola con queste tortuosità. Accettiamo che le previsioni dell’equazione di Schrödinger sono reali. Entrambe le parti della funzione d’onda finale sono effettivamente presenti. Si limitano a descrivere mondi separati, che non interagiranno mai piú.

Everett non introdusse nulla di nuovo nella meccanica quantistica; rimosse dal suo formalismo alcuni pezzi goffi ed estranei. Qualunque versione non everettiana della meccanica quantistica è, per dirla con il fisico Ted Bunn, una teoria dei «mondi che scompaiono». Se i molti mondi vi preoccupano, per eliminarli dovreste ritoccare o la natura degli stati quantistici o la loro normale evoluzione. Ne vale la pen...

Indice dei contenuti

• Copertina
• Frontespizio
• Prologo. Non abbiate paura
• Qualcosa di nascosto a fondo
• Parte prima. Inquietante
• Parte seconda. Divisione
• Parte terza. Spaziotempo
• Epilogo. Tutto è quantistico
• Appendice. La storia delle particelle virtuali
• Ringraziamenti
• Ulteriori letture
• Riferimenti bibliografici
• Indice analitico
• Il libro
• L’autore
• Copyright