La strada che porta alla realtà

Roger Penrose

• Editore: BUR
• Anno: 2020
• Print ISBN: 9788817103008
• eBook ISBN: 9788831802192
• Argomento: Scienze fisiche
• Categoria: Ricerche e metodologie scientifiche

Oltre tre millenni di conquiste scientifiche in un unico, grande disegno: ecco l'ambizioso scopo di questo caposaldo della divulgazione, che ci conduce alla scoperta della vera natura di spazio e tempo attraverso la stupefacente armonia tra i dati fisici e le idee matematiche che li interpretano. Grazie a un'indiscussa capacità divulgativa, Penrose rende accessibili e intriganti i segreti dell'universo, permettendoci di contemplare in un quadro unitario gli elementi che regolano il delicatissimo equilibrio della nostra esistenza: i "mattoni costitutivi" della realtà. Con una scrittura accattivante, grande precisione e una dose di preziosa ironia, Penrose affronta i misteri della natura, da elementi microscopici quali i quark fino a fenomeni meno conosciuti dello spazio, come i buchi neri. Un'imperdibile introduzione alle leggi del mondo in cui viviamo, per ripercorrere la sfida intellettuale che ha dischiuso all'uomo i meccanismi dell'universo.

1

Le radici della scienza

1.1 La ricerca delle forze che modellano il mondo

Quali sono le leggi che governano il nostro universo? Con quali mezzi possiamo conoscerle? In quale modo una simile conoscenza ci aiuta a comprendere e forse a influenzare il mondo?

Sin dall’alba dell’umanità gli esseri umani sono stati profondamente interessati a domande come queste. Dapprima avevano cercato di comprendere le influenze che controllano il mondo rifacendosi a quelle cognizioni che la loro epoca metteva loro a disposizione. Avevano immaginato che qualunque cosa o chiunque controllasse il loro ambiente l’avrebbe fatto nello stesso modo con cui essi stessi si sarebbero sforzati di controllare le cose: inizialmente pensarono dunque che il loro destino fosse sotto l’influenza di Esseri che agivano in perfetto accordo con i loro propri impulsi umani. Impulsi quali l’orgoglio, l’amore, l’ambizione, la rabbia, la paura, la vendetta, la passione, il castigo, la lealtà, la capacità artistica. Di conseguenza, il corso degli eventi naturali – come la luce del sole, la pioggia, la tempesta, la carestia, la malattia o la pestilenza – avrebbe seguito i capricci di Dei o Dee spinti a loro volta da pulsioni umane. E la sola azione capace di esercitare un’influenza su questi eventi era l’appagamento degli Dei.

Gradualmente però schemi di differente natura cominciarono a dimostrarsi attendibili. L’esattezza del movimento del Sole nel cielo e l’evidente correlazione con l’alternarsi di giorno e notte offrirono l’esempio più ovvio; ma si vide anche che la posizione del Sole rispetto alla sfera celeste delle stelle era strettamente associata alla inarrestabile e regolare variazione delle stagioni, con una conseguente chiara influenza sul clima e sul comportamento della vegetazione e degli animali. Anche il movimento della Luna sembrava essere rigorosamente controllato, con le sue fasi determinate dalla sua relazione geometrica con il Sole. In quelle regioni del pianeta dove i mari aperti incontravano la terra, si notò che le maree avevano una regolarità strettamente governata dalla posizione (e fase) della Luna. Infine anche i moti apparenti dei pianeti, molto più complicati, cominciarono a svelare i loro segreti, rivelando un’estrema precisione e regolarità alla loro base. Se i Cieli erano davvero controllati dai capricci degli Dei, allora sembrava che gli stessi Dei agissero sotto l’incantesimo di precise leggi matematiche.

Allo stesso modo, le leggi che controllano alcuni fenomeni terrestri e che sembravano influenzate dai Cieli – come le variazioni giornaliere e annuali di temperatura, il flusso e riflusso degli oceani, la crescita delle piante – condividevano la regolarità matematica che sembrava guidare gli Dei. Ma questa relazione tra corpi celesti e comportamento terreno potrebbe apparire a volte esagerata o mal compresa e di conseguenza assumere un’importanza eccessiva, portando così agli aspetti occulti e mistici dell’astrologia. Furono necessari molti secoli prima che il rigore del sapere scientifico permettesse di districare le vere influenze dei Cieli da quelle puramente ipotetiche e mistiche. Fu tuttavia evidente fin dai primissimi tempi che simili influenze esistevano davvero e che, di conseguenza, le leggi matematiche dei Cieli devono avere importanza anche sulla Terra.

In modo apparentemente indipendente da ciò, si percepì che vi erano altre regolarità nel comportamento degli oggetti terrestri. Una di queste era la tendenza di tutte le cose in una stessa zona a muoversi nella medesima direzione verso il basso, conformemente all’influenza che adesso chiamiamo gravità. Si osservò che qualche volta la materia si trasformava da una forma in un’altra, come nel caso della fusione del ghiaccio o dello scioglimento del sale, ma sembrava che la quantità totale di quella materia non cambiasse mai; questa è la legge che adesso chiamiamo conservazione della massa. Si notò inoltre che vi erano molti corpi materiali che avevano l’importante proprietà di mantenere la loro forma, fenomeno che fece sorgere l’idea di moto spaziale rigido. Divenne così possibile comprendere le relazioni spaziali in termini di una precisa e ben definita geometria – la geometria tridimensionale che adesso chiamiamo euclidea. Per di più, risultò che la nozione di «linea retta» in questa geometria era la medesima che era offerta dai raggi luminosi (o linee di mira). Queste idee possedevano una notevole precisione e bellezza ed ebbero grande fascino per gli antichi, proprio come per noi adesso.

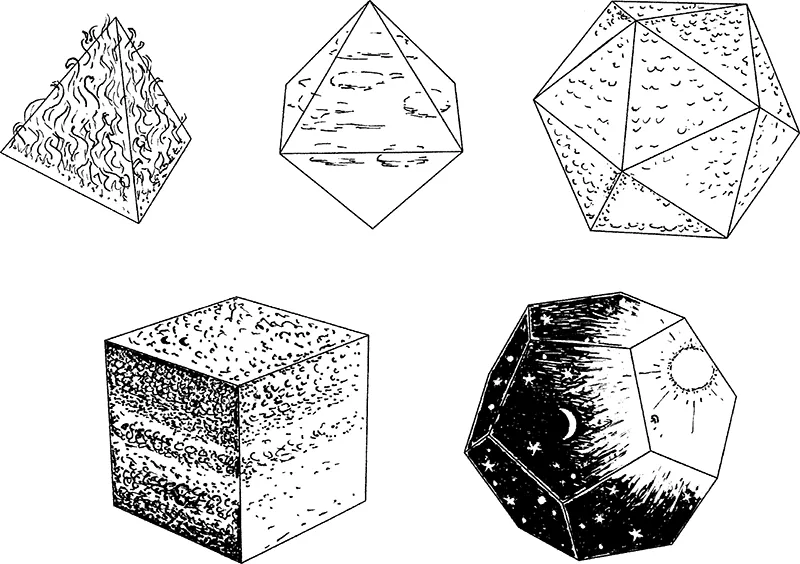
Tuttavia, riguardo alla vita di ogni giorno, le implicazioni di questa precisione matematica per le azioni del mondo spesso apparivano banali e limitate, nonostante la matematica di per sé sembrasse rappresentare una profonda verità. Di conseguenza nei tempi antichi molte persone, affascinate dall’argomento, si fecero trasportare dall’immaginazione. In astrologia, per esempio, le figure geometriche spesso assunsero connotazioni mistiche e occulte, come i presunti poteri magici di pentagrammi ed eptagrammi. Si tentò persino di mettere in relazione, in modo del tutto ipotetico, i solidi platonici e gli stati elementari fondamentali della materia (vedi fig. 1.1). Così per molti secoli non si poté arrivare alle profonde conoscenze che ora abbiamo riguardo alle vere relazioni tra massa, gravità, geometria, moto planetario e comportamento della luce.

Fig. 1.1 - Un’associazione puramente di fantasia fatta dai Greci antichi tra i cinque solidi platonici e i quattro «elementi» (fuoco, aria, acqua e terra),assieme al firmamento celeste rappresentato dal dodecaedro.

1.2 Verità matematica

I primi passi verso la comprensione delle vere influenze che controllano la Natura richiedevano di districare il vero dal puramente ipotetico. Ma gli antichi dovevano raggiungere altri risultati, prima di essere in grado di comprendere la Natura: quello che dovevano fare era innanzitutto scoprire il modo di districare il vero dall’ipotetico in matematica. Era necessario un procedimento per dire se una data affermazione matematica può essere ritenuta vera o meno. E finché tale questione preliminare non fosse stata determinata in modo ragionevole, vi sarebbe stata ben poca speranza di dedicarsi seriamente ai problemi più difficili, riguardanti le forze che controllano l’effettivo comportamento del mondo e le loro diverse relazioni con la verità matematica. La chiave per comprendere la Natura si trovava infatti in una matematica irrefutabile: la percezione di questo fatto fu forse la prima grande conquista della scienza.

Sebbene verità matematiche di vario genere fossero state congetturate sin dai tempi degli antichi Egizi e dei Babilonesi, la prima solida pietra angolare della comprensione matematica – e quindi della scienza stessa – fu posta soltanto quando i grandi filosofi greci Talete di Mileto (c. 625-c. 547 a. C.) e Pitagora¹ di Samo (c. 572-497 a. C.) introdussero la nozione di dimostrazione matematica. Sembra che Talete sia stato il primo a parlare della nozione di dimostrazione, ma che fu Pitagora il primo a utilizzarla per dimostrare cose che altrimenti non sarebbero state ovvie. Sembra anche che Pitagora abbia avuto la grande intuizione dell’importanza del numero e dei concetti aritmetici per il controllo delle azioni del mondo fisico. Si dice che giunse alla sua intuizione osservando la relazione tra le più belle armonie prodotte da lire e flauti e i semplici rapporti tra le lunghezze di corde vibranti o di tubi. Si dice anche che a lui si debba l’introduzione della «scala pitagorica», i cui rapporti numerici costituiscono le frequenze che determinano gli intervalli principali su cui è basata sostanzialmente la musica occidentale.² Il famoso teorema di Pitagora, che afferma che il quadrato costruito sull’ipotenusa di un triangolo rettangolo è uguale alla somma dei quadrati costruiti sugli altri due lati, mostra, forse più di qualunque altra cosa, che vi è davvero una precisa relazione tra l’aritmetica dei numeri e la geometria dello spazio fisico (vedi capitolo 2).

Pitagora ebbe una numerosa comunità di seguaci – i Pitagorici – nella città di Crotone, ma la loro influenza sul mondo esterno fu ostacolata dal fatto che tutti i membri avevano giurato di mantenere il segreto. Di conseguenza, molte delle loro dettagliate conclusioni sono andate perse: solo alcune di queste erano trapelate ugualmente, con disastrose conseguenze per le «talpe», in almeno un’occasione uccise per annegamento!

Nel lungo periodo, l’influenza dei Pitagorici sul progresso del pensiero umano è stata enorme. Per la prima volta, con la dimostrazione matematica, era possibile fare affermazioni significative di natura inconfutabile, così che esse sarebbero tanto vere oggi quanto lo erano al momento della loro formulazione, a prescindere da come la nostra conoscenza del mondo sia progredita da allora. La vera natura eterna della matematica stava cominciando a rivelarsi.

Ma che cos’è una dimostrazione? Una dimostrazione, in matematica, è un argomento ineccepibile che, impiegando soltanto i metodi del puro ragionamento logico, permette di dedurre la validità di una data asserzione matematica dalla validità, già stabilita, di altre asserzioni matematiche e da certe affermazioni primitive – gli assiomi – la cui validità è ritenuta evidente. Una volta che una simile asserzione matematica è stata stabilita in questo modo, è chiamata teorema.

Molti dei teoremi cui i Pitagorici erano interessati erano di natura geometrica. Altri erano semplicemente asserzioni sui numeri. Quelli che riguardavano soltanto numeri hanno una validità inequivocabile anche oggi, proprio come l’avevano al tempo di Pitagora. Cosa dire dei teoremi geometrici che i Pitagorici avevano ottenuto usando i loro procedimenti di dimostrazione matematica? Anch’essi hanno una chiara validità oggigiorno, eppure c’è un problema a complicare le cose. È una questione la cui natura è più comprensibile a noi, dal nostro moderno osservatorio privilegiato, rispetto a quanto lo fosse al tempo di Pitagora. Gli antichi conoscevano solo un tipo di geometria, in altre parole quella che ora chiamiamo geometria euclidea, ma adesso noi ne conosciamo molti altri tipi. Così, nel prendere in considerazione i teoremi geometrici dell’antica Grecia, diventa importante specificare che la nozione di geometria cui ci si riferisce è proprio la geometria di Euclide. (Nel § 2.4, dove sarà dato un esempio importante di geometria non euclidea, sarò più esplicito su tali questioni.)

La geometria euclidea è una specifica struttura matematica, con propri specifici assiomi (che includono alcune asserzioni meno sicure, chiamate postulati), che offriva un’eccellente approssimazione di un particolare aspetto del mondo fisico. Questo era l’aspetto di realtà, ben familiare agli antichi greci, che faceva riferimento alle leggi che reggono la geometria di oggetti rigidi e le loro relazioni con altri oggetti rigidi, quando sono mossi nello spazio tridimensionale. Alcune di queste proprietà erano così familiari e coerenti che tendevano a essere ritenute verità matematiche «ovvie» ed erano prese come assiomi (o postulati). Come vedremo nei capitoli 17-19 e nei §§27.8 e 27.11, la relatività generale di Einstein – e anche la geometria di Minkowsky della relatività speciale – forniscono geometrie per l’universo fisico che sono diverse, ma tuttavia più precise della pur straordinariamente precisa geometria di Euclide. Dobbiamo quindi valutare bene, quando prendiamo in considerazione asserzioni geometriche, se sia possibile credere che gli «assiomi» siano, in qualsiasi senso, effettivamente veri.

Ma che cosa significa «vero» in questo contesto? Questa difficile questione fu apprezzata dal grande filosofo greco Platone che visse ad Atene circa dal 429 a. C. al 347 a. C., più o meno un secolo dopo Pitagora. Platone chiarì che le asserzioni matematiche – le cose che potevano essere ritenute incontestabilmente vere – si riferivano non a effettivi oggetti fisici (come gli approssimativi quadrati, triangoli, cerchi, sfere e cubi che potevano essere disegnati sulla sabbia, o costruiti con legno o pietra) ma a certe entità idealizzate, o idee. Egli immaginò che queste entità ideali abitassero un altro mondo, distinto dal mondo fisico. Oggigiorno possiamo fare riferimento a questo mondo come al mondo platonico delle forme matematiche. Le strutture fisiche, come i quadrati, i cerchi o i triangoli ritagliati dal papiro o tracciati su una superficie piatta, o forse i cubi, i tetraedri o le sfere scolpiti nel marmo, potrebbero essere rigorosamente conformi a questi ideali, ma soltanto in modo approssimato. I reali quadrati, cubi, cerchi, sfere, triangoli matematici non farebbero parte del mondo fisico, ma risiederebbero nel mondo matematico delle forme idealizzate di Platone.

1.3 Il mondo matematico di Platone è «reale»?

Questa fu un’idea straordinaria per quell’epoca, e si è rivelata molto potente. Ma il mondo matematico platonico esiste effettivamente, in qualsiasi senso? Molti tra filosofi e persone comuni potrebbero ritenere un simile «mondo» una perfetta finzione, un esclusivo prodotto della nostra sfrenata immaginazione. Tuttavia il punto di vista platonico ha davvero un immenso valore. Ci dice di prestare attenzione a distinguere le esatte entità matematiche dalle approssimazioni che vediamo intorno a noi nel mondo delle cose fisiche. Inoltre ci fornisce lo schema in base al quale la scienza moderna ha proceduto da allora. Gli scienziati suggeriscono modelli del mondo – o piuttosto di certi aspetti del mondo – e questi modelli possono essere testati contro osservazioni precedenti e contro i risultati di esperimenti accuratamente progettati. I modelli sono ritenuti appropriati se superano questi rigorosi esami e se, oltre a ciò, sono strutture internamente coerenti. Per la nostra attuale discussione, il punto importante riguardo questi modelli è che essi sono fondamentalmente modelli matematici puramente astratti. La questione stessa della coerenza interna di un modello scientifico, in particolare, richiede che il modello sia esattamente specificato. Questa precisione esige che il modello sia matematico, perché altrimenti non si può essere sicuri che tali questioni abbiano risposte ben definite.

Se al modello in sé viene assegnato qualsiasi genere di «esistenza», allora questa esistenza è collocata nel mondo platonico delle forme matematiche. Naturalmente, si potrebbe assumere un punto di vista opposto: e precisamente che il modello in sé esista soltanto nelle nostre menti, invece di ritenere che il mondo di Platone sia in un qualsiasi senso assoluto e «reale». Tuttavia si possono raggiungere significativi risultati postulando che le strutture matematiche abbiano una propria realtà. Le nostre menti individuali, infatti, sono notoriamente imprecise, inaffidabili e incoerenti nei loro giudizi. La precisione, l’affidabilità e la coerenza, che le nostre teorie scientifiche richiedono, esigono qualcosa che vada oltre ciascuna delle nostre labili menti individuali. Nella matematica troviamo una consistenza decisamente maggiore rispetto a quella che può trovarsi in una qualunque mente particolare. Tutto ciò non si rivolge a qualcosa al di fuori di noi e a una realtà che si trova al di là di ciò che ciascun individuo può raggiungere?

Nonostante ciò, si potrebbe ancora assumere il punto di vista alternativo che il mondo matematico non abbia alcuna esistenza indipendente e consista soltanto di certe idee, distillate dalle nostre menti, talmente degne di fiducia che hanno conquistato il consenso di tutti. Ma anche questo punto di vista è manchevole sotto molti riguardi. Il «co...

Indice dei contenuti

• Copertina
• Frontespizio
• Prefazione
• Notazione
• Prologo
• 1. Le radici della scienza
• 2. Un antico teorema e una questione moderna
• 3. Tipi di numero nel mondo fisico
• 4. I magici numeri complessi
• 5. La geometria di logaritmi, potenze e radici
• 6. Il calcolo infinitesimale nel campo reale
• 7. Calcolo infinitesimale con numeri complessi
• 8. Superfici di Riemann e applicazioni complesse
• 9. Sviluppo in serie di Fourier e iperfunzioni
• 10. Superfici
• 11. Numeri ipercomplessi
• 12. Varietà di n dimensioni
• 13. Gruppi di simmetria
• 14. Calcolo infinitesimale sulle varietà
• 15. Fibrati e connessioni di gauge
• 16. La scala dell’infinito
• 17. Lo spaziotempo
• 18. La geometria di Minkowski
• 19. I campi classici di Maxwell ed Einstein
• 20. Lagrangiane e hamiltoniane
• 21. La particella quantistica
• 22. Algebra, geometria e spin quantistici
• 23. Il mondo quantistico entangled
• 24. L’elettrone di Dirac e le antiparticelle
• 25. Il modello standard della fisica delle particelle
• 26. La teoria quantistica dei campi
• 27. Il Big Bang e il suo retaggio termodinamico
• 28. Teorie speculative sull’universo primordiale
• 29. Il paradosso della misura
• 30. Il ruolo della gravità nella riduzione dello stato quantico
• 31. Supersimmetria, sopradimensionalità e stringhe
• 32. Il cammino più rigoroso di Einstein; le variabili di loop
• 33. Prospettive più radicali; teoria dei twistor
• 34. Dove si trova la strada verso la realtà?
• Epilogo
• Ringraziamenti
• Bibliografia
• Copyright