Istanti fatali

Quando i numeri hanno spiegato il mondo

Umberto Bottazzini

• Editore: Editori Laterza
• Anno: 2021
• eBook ISBN: 9788858144695
• Argomento: Scienze sociali
• Categoria: Storia della scienza

Il libro di Bottazzini si legge come un lungo e piacevole racconto e in esso si comprende perché in matematica il progresso non scenda dal cielo, né proceda in maniera lineare; anzi, il più delle volte, necessiti di uno scatto di genio.Armando Torno, "Il Sole 24 Ore"

Questo non è un libro di storia della matematica, ma un libro di racconti matematici. La sua trama e il suo ordito sono le storie che circondano i numeri e le scoperte che attraverso di essi abbiamo potuto fare, e che risalgono fino agli albori del pensiero.

Leggendo questo libro scoprirete che è vero quello che diceva a proposito della matematica l'americana del romanzo Altezza reale di Thomas Mann: «Non saprei immaginare niente di più divertente. È un gioco dell'aria, per dir così. Anzi, addirittura fuori dell'aria».

Il quadro e il tondo

IL BACINO DEL TEMPIO E I CAMPI DELLO SCRIBA

“Madama... veramente... in questo mondo / conciossiacosaquandofosseché / il quadro non è tondo...”, balbetta Leporello a Donna Elvira prima di squadernare, in una delle più celebri arie di Mozart, il “catalogo” delle “donnesche imprese” di Don Giovanni, l’elenco “delle belle che amò il padron mio”. Che un quadrato non sia rotondo è dunque una banalità che conosce pure un semplice servitore di fine Settecento. Tuttavia, nelle parole che il librettista Lorenzo Da Ponte mette in bocca a Leporello c’è forse qualcosa di più dell’esigenza di una facile rima. C’è forse l’allusione a una faccenda che, da che mondo è mondo, è irrisolta tanto da diventare sinonimo di cosa impossibile, vana e degna di riso. Si tratta della quadratura del cerchio, in altre parole, del problema di costruire un quadrato di area uguale a quella di un cerchio dato.

Perché mai preoccuparsi di costruire un simile quadrato, e non per esempio un triangolo o un rettangolo? Perché tra tutte le figure non c’è dubbio che il quadrato sia quella più semplice e facile da misurare. Per calcolarne l’area basta conoscere la lunghezza del lato. Ecco perché fin dall’antichità si è pensato che, per misurare l’area del cerchio, la cosa da farsi fosse paragonarlo a un quadrato, determinare il quadrato cui era equivalente. E, in questo modo, poter misurare l’area del cerchio con la stessa esattezza con cui si calcola l’area di un triangolo, di un rettangolo o di un qualunque poligono.

Con ogni probabilità, quando scrive il Don Giovanni (1787) Da Ponte è all’oscuro di queste sottigliezze geometriche. È poeta di corte dell’imperatore Giuseppe II a Vienna, e si dice che per il libretto si sia avvalso del contributo di un esperto del genere come Giacomo Casanova, anche se forse non ne aveva un gran bisogno. Infatti, è un libertino conclamato, bandito dalla Serenissima Repubblica di Venezia dopo una condanna per “pubblico concubinaggio e sequestro di una donna rispettabile”, condita con l’accusa di aver vissuto e organizzato allegri convivi in un bordello e aver avuto un paio di figli da un’amante. Comportamento poco commendevole, soprattutto se si tratta di un sacerdote, come nel caso di Da Ponte, prete della parrocchia di San Luca a Venezia. Nato come Emanuele Conegliano nel ghetto di Ceneda, convertito ancora adolescente al cattolicesimo dal vescovo della locale diocesi che gli ha imposto il proprio nome, ha poi frequentato il seminario fino a prendere i voti. Dev’essere dunque familiare con le Scritture. E forse non ha dimenticato un passo del I Libro dei Re che riguarda la nostra questione.

Quando si parla del tempio fatto costruire dal re Salomone, si racconta che il re fece chiamare da Tiro un uomo capace di ogni genere di lavori in bronzo e, dice la Bibbia, costui “fece il Mare, un bacino di metallo fuso di dieci cubiti da un orlo all’altro, perfettamente rotondo; la sua altezza era di cinque cubiti e una corda di trenta cubiti lo poteva cingere intorno”. Quel bacino, chiamato il Mare, serviva per le abluzioni dei sacerdoti. Stando al testo biblico che risale al 550 a.C., se una corda di 30 cubiti cinge un bacino del diametro di 10 cubiti vuol dire che, all’epoca, presso gli ebrei si stimava che la circonferenza di un cerchio fosse tre volte il diametro.

Cosa c’entra il rapporto tra la lunghezza della circonferenza e quella del diametro con la quadratura del cerchio? C’entra, e la ragione dipende da una caratteristica peculiare del cerchio che ci hanno insegnato a scuola: tra l’area del cerchio e la lunghezza della sua circonferenza intercorre uno stretto legame, per cui conoscendo l’area si ricava anche la lunghezza della circonferenza, e viceversa. Infatti, entrambe quelle grandezze dipendono da un numero che è sempre lo stesso, qualunque sia il cerchio e qualunque sia la circonferenza. Prendete pure un cerchio, grande o piccolo, a vostra scelta: la sua area è proporzionale al quadrato del raggio, qualunque sia il valore del raggio, e la lunghezza della circonferenza è proporzionale al diametro. La costante di proporzionalità è la stessa. È sempre lo stesso numero. Straordinario, non vi pare?

Determinando quel numero si risolvono sia il problema della quadratura del cerchio sia quello della rettificazione della circonferenza, come si chiama talvolta il problema di trovare un segmento rettilineo lungo quanto la circonferenza. Infatti, solo i segmenti rettilinei sono misurabili in maniera precisa. Per misurare gli archi di curva in maniera altrettanto precisa occorre dunque poterli ‘rettificare’, ossia trasformarli in un segmento rettilineo di pari lunghezza. Certo Da Ponte non ne è al corrente, ma da qualche decennio un grande matematico dell’Accademia delle scienze di Pietroburgo, Leonhard Euler – che in latino, la lingua internazionale dell’epoca, firma i suoi lavori come Eulerus diventato Eulero in italiano – ‘per brevità’ ha cominciato a denotare quel numero con la lettera greca π, simbolo rimasto in uso da allora. Si tratta solo di un simbolo, perché nemmeno Eulero, uno dei più grandi matematici di ogni epoca, era in grado di calcolare con esattezza quel numero.

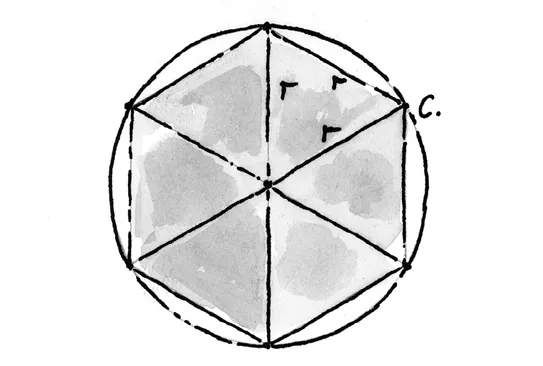
Per gli ebrei del I Libro dei Re π è uguale a 3, ma altrove stime molto migliori sono note da tempo. Ne offre un esempio una tavoletta babilonese che risale a circa quattromila anni fa ed è stata ritrovata nel 1936 negli scavi della città di Susa, a circa 300 km dal sito dell’antica Babilonia. Si vede un esagono regolare inscritto in una circonferenza. Lo scriba si limita a dire che il rapporto tra il perimetro dell’esagono e quello della circonferenza è dato da un numero che, nella notazione sessagesimale babilonese, si scrive come 57/60 + 36/60².

Come ha fatto a scoprirlo? I Babilonesi sapevano bene, e la tavoletta ce lo mostra, che il perimetro dell’esagono è 6 volte il raggio della circonferenza o, in altre parole, 3 volte il diametro, e conoscevano che la lunghezza della circonferenza è proporzionale al diametro. Tradotto in termini a noi più familiari, tutto questo significa che, per ottenere il suo risultato, lo scriba deve aver stimato che il numero che indichiamo con π, la costante di proporzionalità tra circonferenza e diametro, è uguale a 3 + 1/8 ossia, π = 3,125.

Anche gli antichi Egizi si erano confrontati con lo stesso tipo di problemi. Lo racconta lo scriba Ahmes nel suo papiro, che promette di iniziarci alla “conoscenza di tutte le cose esistenti e di tutti gli oscuri segreti”. Siamo intorno al 1650 a.C. ma Ahmes afferma di copiare da un testo che risale a molto prima, tra il 1800 e il 2000 a.C. E qual è la stima del valore del rapporto tra circonferenza e diametro adottata per i calcoli?

La vediamo all’opera nel problema 50, che chiede di determinare l’area di un campo rotondo di diametro 9 khet (il khet è un’unità di misura delle lunghezze che vale all’incirca 52 metri). A parte la singolarità di immaginare nella realtà un campo di quella forma, la regola dello scriba dice di accorciare il diametro di 1/9 per ottenere il lato del quadrato che risolve il problema. In altre parole, l’area del campo rotondo è uguale a quella di un quadrato di lato 8 khet. Ahmes non spiega perché, né come è giunto a un risultato. La sua è una regola empirica, forse figura tra “gli oscuri segreti” rivelati dal papiro. Come forse vi figura il fatto che è sempre la stessa costante che intercorre tra l’area del cerchio e il quadrato del raggio, e tra la lunghezza della circonferenza e il suo diametro, di cui lo scriba è ben consapevole. La sua regola implica che il rapporto tra l’area del cerchio e il quadrato del raggio è 4 × (8/9)², e dunque π ha il valore approssimato 3,16.

Commentando questo risultato, che apprende da un pionieristico libro di Otto Neugebauer sulla matematica dell’antichità, in una delle lettere che abbiamo visto scambiare col fratello André, Simone Weil osserva che “pare abbastanza facile da immaginare, supponendo metodi molto grossolani” come quelli verosimilmente usati da Ahmes. Supponiamo, dice la filosofa francese, di dividere il quadrato (di lato 9 khet) circoscritto al cerchio in 81 quadratini. “Per avere l’area del cerchio, bisogna sottrarre tre di questi quadratini più il valore pressappoco di tre mezzi quadratini per ogni angolo” del quadrato circoscritto. La procedura empirica immaginata da Simone Weil non è molto lontana da quella che deve aver seguito Ahmes, che ha già suggerito un procedimen...

Indice dei contenuti

• Prologo
• Contare il tempo e... le cose
• Uno zero per nulla
• La scoperta dei numeri irrazionali
• Il quadro e il tondo
• I numeri immaginari
• L’universo non euclideo
• Epilogo
• Qualche ulteriore lettura