
eBook - ePub
Smile Pricing Explained
P. Austing
This is a test
Condividi libro
- English
- ePUB (disponibile sull'app)
- Disponibile su iOS e Android
eBook - ePub
Smile Pricing Explained
P. Austing
Dettagli del libro
Anteprima del libro
Indice dei contenuti
Citazioni
Informazioni sul libro
Smile Pricing Explained provides a clear and thorough explanation of the concepts of smile modelling that are at the forefront of modern derivatives pricing. The key models used in practice are covered, together with numerical techniques and calibration.
Domande frequenti
Come faccio ad annullare l'abbonamento?
È semplicissimo: basta accedere alla sezione Account nelle Impostazioni e cliccare su "Annulla abbonamento". Dopo la cancellazione, l'abbonamento rimarrà attivo per il periodo rimanente già pagato. Per maggiori informazioni, clicca qui
È possibile scaricare libri? Se sì, come?
Al momento è possibile scaricare tramite l'app tutti i nostri libri ePub mobile-friendly. Anche la maggior parte dei nostri PDF è scaricabile e stiamo lavorando per rendere disponibile quanto prima il download di tutti gli altri file. Per maggiori informazioni, clicca qui
Che differenza c'è tra i piani?
Entrambi i piani ti danno accesso illimitato alla libreria e a tutte le funzionalità di Perlego. Le uniche differenze sono il prezzo e il periodo di abbonamento: con il piano annuale risparmierai circa il 30% rispetto a 12 rate con quello mensile.
Cos'è Perlego?
Perlego è un servizio di abbonamento a testi accademici, che ti permette di accedere a un'intera libreria online a un prezzo inferiore rispetto a quello che pagheresti per acquistare un singolo libro al mese. Con oltre 1 milione di testi suddivisi in più di 1.000 categorie, troverai sicuramente ciò che fa per te! Per maggiori informazioni, clicca qui.
Perlego supporta la sintesi vocale?
Cerca l'icona Sintesi vocale nel prossimo libro che leggerai per verificare se è possibile riprodurre l'audio. Questo strumento permette di leggere il testo a voce alta, evidenziandolo man mano che la lettura procede. Puoi aumentare o diminuire la velocità della sintesi vocale, oppure sospendere la riproduzione. Per maggiori informazioni, clicca qui.
Smile Pricing Explained è disponibile online in formato PDF/ePub?
Sì, puoi accedere a Smile Pricing Explained di P. Austing in formato PDF e/o ePub, così come ad altri libri molto apprezzati nelle sezioni relative a Business e Servizi finanziari. Scopri oltre 1 milione di libri disponibili nel nostro catalogo.
Informazioni
Argomento
BusinessCategoria
Servizi finanziari1 | Introduction to Derivatives |
1.1 Hedging with Forward Contracts
A derivative is any financial product that is derived from a simpler underlying asset. The simplest derivative is a forward contract. For example, it could be a forward contract on wheat. A grower in England plants a field of wheat, and goes to significant expense in buying seed and fertiliser and maintaining the crop. This makes sense because of the current value of wheat. However, unfortunately, an excellent growing season in France means that there is a glut of wheat on the market just at the time he has harvested and needs to sell, and the price he can achieve is much lower than expected. This could be disastrous.
To avoid this situation, the grower could enter into a forward contract with his client, a cereal producer. At the time of sowing, the grower agrees with the cereal company to sell ten tonnes of wheat at a price K pounds per tonne, to be delivered within a given short interval in, say, six months’ time. The grower is happy because he knows what price he will achieve for the wheat, and can budget appropriately. If the market view on the future price of wheat is too low, the grower can look at the forward price of other crops, and plant something else. If at the delivery time the value of wheat has gone up, he will regret missing out, but on the other hand if the price has dropped he will have avoided ruin.
Meanwhile, the cereal company is happy because it knows in advance it can obtain enough wheat at a reasonable price, even if bad weather conditions lead to low crop yields and high prices at harvest time.
The grower and cereal producer are both acting in the market to hedge their risk. This is the main benefit of using derivatives, and in this way derivatives help to make markets more stable and more efficient. If used wisely, they can prevent bankruptcies and job losses in times of sudden market stress.
This example can also illustrate some of the risks in using derivatives. What if, due to a bad growing season, the grower is unable to deliver ten tonnes of wheat? Then, since he has entered into a firm obligation to deliver the crop, he would have to go into the market and purchase enough to make up his delivery. Assuming other participants in the market had also experienced poor conditions, this could be ruinously expensive. So in reality, the grower ought only to enter into the contract for a quantity of wheat he is absolutely certain he can deliver, even in the worst possible case.
1.2 Speculation with Forward Contracts
A second, entirely different, participant in the market is a wealthy individual who does not own, nor have any capacity to grow, wheat. However, she has the strong view that, due to political problems in an important wheat growing country, the price of wheat will increase. She wishes to profit from the increase in price without any outlay now. So she enters into a forward contract to buy N tonnes of wheat at a price K at a future time T (say one year’s time). If the price has risen, she will immediately sell the wheat and make a profit

where ST is the price of wheat at the expiry time T of the contract. Needless to say, if the price has fallen, she makes a loss.
In reality, the speculator does not want to be bothered with receiving and then delivering N tonnes of wheat, and so she will close out the contract before the delivery date. That is, she will either sell the contract, or enter into an opposite contract. Alternatively, she may have originally entered into a cash settled contract with a third party. This third party will handle the buying and selling of contracts, and at the expiry simply pay the cash profit (or demand payment of the loss). Banks perform this kind of service in huge volumes, not necessarily for wheat contracts, but certainly for contracts in shares (equities), foreign currencies (FX), and precious metals, oil or energy (commodities).
In the jargon of derivatives, St is the spot price or simply spot at time t, namely the value of the asset in the open market at time t. The quantity N is known as the notional amount, since from the point of view of a speculator entering into a cash settled transaction, the cash flow of NK agreed for the commodity never actually takes place. The agreed price in the contract, K, is known as the strike price, since it is the price at which the deal is struck.
1.3 Arbitrage
The third type of participant in the market aims to make money by arbitrage. An arbitrage opportunity arises when it is possible to make money without any risk. In the simplest example, let’s suppose an investor notices that it is possible to buy wheat contracts on one exchange for 59 US dollars and to sell on another for 62 dollars. Then he can make an instant profit by simultaneously buying on one and selling on the other.
If arbitrage exists in a market, then very quickly prices will be forced up in the underpriced asset as buyers charge in, and prices will be forced down on the overpriced asset as more and more people sell on that exchange. This does not mean that in an efficient market arbitrage never exists. Usually though, it only exists for a fleeting moment, until it is eliminated by the most sophisticated investors.
The concept of arbitrage is fundamental in pricing derivatives contracts. A quant1 working for a bank will often be asked to price a new style of exotic derivative. If the price she comes up with can be demonstrated to be arbitrageable against other liquid assets in the market, then the bank will certainly lose money. Let’s suppose that this particular bank has an electronic dealing system in, say, foreign exchange derivatives. When outsiders spot the arbitrage, they will continually buy the liquid assets and sell the new exotic derivative, or vice versa, mercilessly making money at the expense of the bank (and no doubt the unfortunate quant).
When we price a derivative, the price must be arbitrage free. We shall see that in many cases, the arbitrage-free price is unique, and so finding it gives the true value of the derivative.
1.4 Vanilla Options
So far, we have looked at the simplest derivative, a forward contract. This is an agreement made now to buy a quantity of some asset at a future date (the expiry date). The deal is struck at the strike price K, and at the expiry time T the payout is

where N is the notional (the quantity of asset), ST is the spot price (value of the underlying asset) at expiry. At any time, this contract has a certain value for a given strike. This value can be positive or negative depending on whether the strike is above or below the market view of the forward value of the asset. Often, the strike will be chosen so that the value is zero when the contract is entered into, and no exchange of money is required between the buyer and seller at the start.
An investor who believes that the asset price will rise may enter into a forward contract to buy at strike K, but what if the asset price actually falls sharply? Her losses could be enormous. So let’s consider a contract that gives her the option, but not the obligation, to buy N units of the asset at strike price K. If, at the expiry time T, the spot price is larger than K then the investor would exercise the option. She could then immediately sell at the prevailing price ST and make profit N(ST – K). On the other hand, if the spot price ends up smaller than the strike, she would certainly not exercise the option. So the payout at expiry is

which we write as

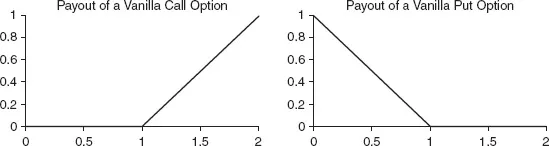
Figure 1.1 Payouts of vanilla call and put options.
This contract is called a vanilla call option. In finance, call means buy and this is an option to buy the asset. The opposite of call is to put, namely to sell. The term vanilla indicates that these are the most basic option contracts. Supposing the investor entered into a contract giving the option to sell the asset at strike price K, that is the investor bought a vanilla put option, the payout would be

The call and put payouts as a function of the spot price at expiry are plotted in Figure 1.1. In these diagrams, the notional is 1 and the strike price 1. As you can see, if you buy a call option, you have limited loss, but unlimited potential gain if spot ends up very high. On the other hand, if you sell a call option, you have unlimited potential liability.
It is now time to whet your appetite for some of the beautiful facts we will soon be encountering. If you are new to this subject, you might well argue that it is impossible to attach a fair value to the contracts that we have been discussing. Imagine we are a bank selling a forward contract, and we cannot find any other counterparty with whom to do the opposite trade to eliminate the risk. Even if we could know in advance the probability distribution of the spot...