A Walk Through Combinatorics

An Introduction to Enumeration and Graph Theory

Mikl??s B??na

• Editore: WSPC
• Anno: 2016
• ISBN:
  9789813148864
• Edizione: 4
• Argomento: Business
• Categoria: Finance

-->

This is a textbook for an introductory combinatorics course lasting one or two semesters. An extensive list of problems, ranging from routine exercises to research questions, is included. In each section, there are also exercises

Chapter 13

Does It Clique? Ramsey Theory

Instead of coloring the vertices of our graphs, in this chapter we will color their edges. We will see that this leads to a completely different set of problems. Our first excursion into the land of infinite graphs is also part of this chapter.

13.1 Ramsey Theory for Finite Graphs

Example 13.1. Six people are waiting in the lobby of a hotel. Prove that there are either three of them who know each other, or three of them who do not know each other.

This statement is far from being obvious. We could think that maybe there is some case in which everyone knows roughly half of the other people, and in the company of any three people there will be two people who know each other, and two people who do not. We will prove, however, that this can never happen.

Solution. (of Example 13.1) Take a K₆ so that each person corresponds to a vertex. Color the edge joining A and B red if A and B know each other, and blue if they do not. Do this for all 15 edges of the graph. The claim of the example will be proved if we can show that there will always be a triangle with monochromatic edges in our graph.

Take any vertex V of our bicolored graph. As V is of degree five, it must have at least three edges adjacent to it that have the same color. Let us assume without loss of generality that this color is red. Let X, Y and Z be the endpoints of three red edges adjacent to V. (The reader can follow our argument in Figure 13.1, where we denoted red edges by solid lines.)

Now if any edge of the triangle XY Z is red, then that edge, and the two edges joining (the endpoints of) that edge to V are red, so we have a triangle with three red edges. If the triangle XY Z does not have a red edge, then it has three blue edges.

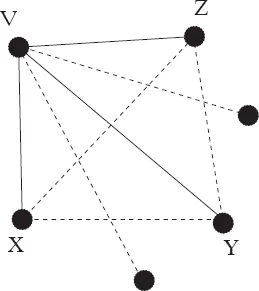
Fig. 13.1 The colors of the edges of the triangle XY Z are crucial.

This beautiful proof is our first example in Ramsey theory. This field is named after Frank Plumpton Ramsey, who was the first person to study this area at the beginning of the twentieth century.

We point out that the result is tight, that is, if there were only five people in the lobby of the hotel, then the same statement would be false. Indeed, take a K₅, and draw it as a regular pentagon and its diagonals. Color all five sides red, and all five diagonals blue. As any triangle in this graph contains at least one side and at least one diagonal, there can be no triangles with monochromatic edges.

Instead of taking a K₆, and coloring its edges red and blue, we could have just taken a graph H on six vertices in which the edges correspond to people who know each other. In this setup, the edges of H correspond to the former red edges, and the edges of the complement of H correspond to the former blue edges. As a complete subgraph is often called a clique, the statement of Example 13.1 can be reformulated as follows. If H is a simple graph on six vertices, then at least one of H and the complement of H contains a clique of size three.

The arguments used in the proof of Example 13.1 strongly depended on the parameter three, the number of people we wanted to know or not to know each other. What happens if we replace this number three by a larger number? Is it true that if there are sufficiently many people in the lobby, there will always be at least k of them who know each other, or k of them who do not know each other? The following theorem answers this question (in fact, a more general one), in the affirmative.

Theorem 13.2 (Ramsey theorem for graphs). Let k and ℓ be two positive integers, both of which is at least two. Then there exists a (minimal) positive integer R(k, ℓ) so that if we color the edges of a complete graph with R(k, ℓ) vertices red and blue, then this graph will either have a K_k subgraph with only red edges, or a K_ℓ subgraph with only blue edges.

Note that any non-empty set of positive integers has a smallest element. Therefore, if we can show that there exists at least one positive integer with the desired property, then we will have shown that a smallest such integer exists.

Example 13.3. Example 13.1, and the discussion after it shows that R(3, 3) = 6. We also have trivial fact R(2, 2) = 2 relating to the graph with one edge.

Proof. (Of Theorem 13.2) We prove the statement by a new version of mathematical induction on k and ℓ. This ...