Energy Geostructures

Innovation in Underground Engineering

Lyesse Laloui, Alice Di Donna, Lyesse Laloui, Alice Di Donna

• Publisher: Wiley-ISTE
• Year: 2013
• Print ISBN: 9781848215726
• eBook ISBN: 9781118761762
• Edition: 1
• Topic: Technology & Engineering
• Subtopic: Civil Engineering
• Index: Technology & Engineering

Energy geostructures are a tremendous innovation in the field of foundation engineering and are spreading rapidly throughout the world. They allow the procurement of a renewable and clean source of energy which can be used for heating and cooling buildings. This technology couples the structural role of geostructures with the energy supply, using the principle of shallow geothermal energy. This book provides a sound basis in the challenging area of energy geostructures.
The objective of this book is to supply the reader with an exhaustive overview on the most up-to-date and available knowledge of these structures. It details the procedures that are currently being applied in the regions where geostructures are being implemented. The book is divided into three parts, each of which is divided into chapters, and is written by the brightest engineers and researchers in the field. After an introduction to the technology as well as to the main effects induced by temperature variation on the geostructures, Part 1 is devoted to the physical modeling of energy geostructures, including in situ investigations, centrifuge testing and small-scale experiments. The second part includes numerical simulation results of energy piles, tunnels and bridge foundations, while also considering the implementation of such structures in different climatic areas. The final part concerns practical engineering aspects, from the delivery of energy geostructures through the development of design tools for their geotechnical dimensioning. The book concludes with a real case study.

Contents

Part 1. Physical Modeling of Energy Piles at Different Scales
1. Soil Response under Thermomechanical Conditions Imposed by Energy Geostructures, Alice Di Donna and Lyesse Laloui.
2. Full-scale In Situ Testing of Energy Piles, Thomas Mimouni and Lyesse Laloui.
3. Observed Response of Energy Geostructures, Peter Bourne-Webb.
4. Behavior of Heat-Exchanger Piles from Physical Modeling, Anh Minh Tang, Jean-Michel Pereira, Ghazi Hassen and Neda Yavari.
5. Centrifuge Modeling of Energy Foundations, John S. McCartney.
Part 2. Numerical Modeling of Energy Geostructures
6. Alternative Uses of Heat-Exchanger Geostructures, Fabrice Dupray, Thomas Mimouni and Lyesse Laloui.
7. Numerical Analysis of the Bearing Capacity of Thermoactive Piles Under Cyclic Axial Loading, Maria E. Suryatriyastuti, Hussein Mroueh, Sébastien Burlon and Julien Habert.
8. Energy Geostructures in Unsaturated Soils, John S. McCartney, Charles J.R. Coccia, Nahed Alsherif and Melissa A. Stewart.
9. Energy Geostructures in Cooling-Dominated Climates, Ghassan Anis Akrouch, Marcelo Sanchez and Jean-Louis Briaud.
10. Impact of Transient Heat Diffusion of a Thermoactive Pile on the Surrounding Soil, Maria E. Suryatriyastuti, Hussein Mroueh and Sébastien Burlon.
11. Ground-Source Bridge Deck De-icing Systems Using Energy Foundations, C. Guney Olgun and G. Allen Bowers.
Part 3. Engineering Practice
12. Delivery of Energy Geostructures, Peter Bourne-Webb with contributions from Tony Amis,
Jean-Baptiste Bernard, Wolf Friedemann, Nico Von Der Hude, Norbert Pralle, Veli Matti Uotinen and Bernhard Widerin.
13. Thermo-Pile: A Numerical Tool for the Design of Energy Piles, Thomas Mimouni and Lyesse Laloui.
14. A Case Study: The Dock Midfield of Zurich Airport, Daniel Pahud.

About the Authors

Lyesse Laloui is Chair Professor, Head of the Soil Mechanics, Geoengineering and CO2 storage Laboratory and Director of Civil Engineering at the Swiss Federal Institute of Technology (EPFL) in Lausanne, Switzerland.
Alice Di Donna is a researcher at the Laboratory of Soil Mechanics at the Swiss Federal Institute of Technology (EPFL) in Lausanne, Switzerland.

PART 1

Physical Modeling of Energy Piles at Different Scales

Chapter 1

Soil Response under Thermomechanical Conditions Imposed by Energy Geostructures

Chapter written by Alice DI DONNA and Lyesse LALOUI.

The foundation of a building represents a connection between the structure and the supporting soil. The mechanical loads coming from the structure are transferred to the soil through it. A number of requirements must be fulfilled to ensure the stability and comfort of the over-structure, the most important of which are (1) the admissible displacements, (2) the acceptable (concrete) stresses and (3) the safety margins with respect to failure [BSI 95]. These aspects are related to the types and properties of the surrounding soils. Data concerning the soil’s response must be collected through a geotechnical survey and represent the basis for the design of the required foundations. Therefore, the behavior of the soil plays a primary role in the design of every geostructure, i.e. every structure that transfers a load to the ground. In the case of energy geostructures, an energy supply role is added to the conventional role of the foundation as a structural support. The foundation is thus subjected to both mechanical and thermal loads transmitted from the piles to the ground. This is the main motivation for understanding and modeling the soil’s response when subjected to a thermomechanical solicitation. In this chapter, the state of knowledge on the thermomechanical behavior of soils is revised within the framework of energy geostructures. A constitutive model capable of reproducing the described behavior is presented and used to study the response of soils subjected to thermal-stress paths typical of the areas around energy piles.

1.1. Introduction

Deep foundations are usually used to limit the settlements of buildings, increase capacity with respect to shallow foundations or reach a more resistant layer of soil when the quality of the surface soil is low. Two stages of the geotechnical design of such foundations are related to the behavior of the surrounding soil: the evaluation of the geotechnical bearing capacity and the prediction of displacements. Starting from the equilibrium of a pile (Figure 1.1), the maximum load Q_LIM that a pile can support is calculated as:

[1.1]

where Q_S is the portion of bearing capacity provided by the friction between the pile and the soil, Q_P is the portion of the bearing capacity provided by the soil below the pile tip and W_P is the pile weight [LAN 99]. A general formula for the calculation of the lateral and base components is:

[1.2]

[1.3]

where H is the pile height,

is the horizontal effective stress normal to the pile–soil interface, δ is the friction angle at the interface, R is the pile radius, Cu is the undrained shear strength, σ_v is the vertical stress at the pile tip and r, ω and z are the radial, circumferential and vertical cylindrical coordinates, respectively. From these equations, it appears that the lateral resistance depends, apart from the friction angle at the interface, on the stress state at the pile–soil interface, while the tip resistance is directly related to the resistance of the soil below the pile.

Figure 1.1. Equilibrium of a pile

When a thermal load is transmitted from a pile to the soil, the latter reacts by changing its volume, and eventually its response, depending on the type of soil. As a result, the temperature variation can affect (positively or negatively) the stress state at the pile–soil interface and the shear strength that governs tip resistance. More significantly, the thermal volume variation in the soil affects the foundation displacement, making it move upward when the soil dilates and downward when it contracts. The entity of the effects induced by the temperature variations on the behavior of the foundation depends on the volume of heated ground and the range of temperature variation. The thermal load imposed by energy piles in current applications is in the range of 2–30°C (see Chapter 3 for data related to current applications), but future developments using the injection of heat in the ground from other technologies, such as solar panels, will lead to higher temperature variations.

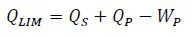
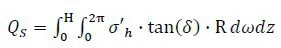
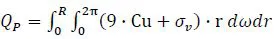
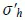
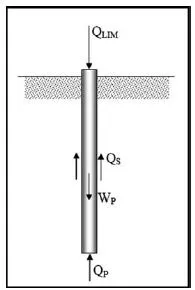
1.2. Thermomechanical behavior of soils

Soils are porous materials made up of a solid skeleton, represented by grains or aggregates, and pores that, in saturated conditions, are filled with water. The case of partial saturation is not considered in this chapter (see Chapter 8 for more details concerning energy piles in unsaturated soils and [FRA 08] for the non-isothermal behavior of unsaturated soils). Soils can be divided into two families: (1) granular (sand and gravel) and (2) fine-grained (silt and clay) materials. Heating a sandy soil in drained conditions results in an increase of volume directly related to the grains’ thermal expansion coefficient. Also, water dilates thermal elastically with a thermal expansion coefficient usually higher than that of grains, but due to drained conditions, the water is free to flow away and does not contribute to the volume variation of the material itself. Table 1.1 provides the thermal expansion coefficients of some minerals and water.

Table 1.1. Volumetric thermal expansion coefficients (T stands for temperature) [MCK 65, DIX 93]

Material	Volumetric thermal expansion coefficient [10^–6°C^–1]
Muscovite	24.8
Kaolinite	29.0
Chlorite	31.2
Illite	25.0
Smectite	39.0
Water	139 + 6.1-T

The response of clays is more complicated and will be discussed in the next section. The complexity of clayey materials’ thermomechanical behavior is a direct consequence of their microstructure and the electrochemical equilibrium between clay particles. Details about this aspect can be found, among others, in [HUE 92].

1.2.1. Thermomechanical behavior of clays

As for granular materials, the two constituents of saturated fine-grained materials (grains/aggregates and water) undergo thermoelastic expansion when heated. However, it has been proved through experimental testing that either a contractive or a dilative volume variation can be observed during heating in drained conditions depending on the load history. The latter is commonly described through the overconsolidation ratio (OCR), defined as:

[1.4]

where

is the preconsolidation stress and

is the current vertical effective stress. The preconsolidation stress is the maximum vertical stress that the soil has already supported (load history). The soil retains a memory of the maximum charge that it has already supported, so that if it is subjected to a load lower than the preconsolidation stress, its deformation is relatively small and, above all, reversible (elastic). If the applied load reaches and surpasses the initial preconsolidation stress, the deformation becomes more significant and, above all, partially irreversible (elastoplastic). In this sense, the preconsolidation stress corresponds to the maximum experienced density (or the lowest void ratio). From a mechanical point of view, it is used to be defined as the limit between the elastic and elastoplastic domains in terms of applied stresses. A soil is considered normally consolidated (NC) if the OCR is within the range of 1 and 2; i.e., if the current load is close to the maximum that the soil has ever supported. Conversely, the material is said to be overconsolidated (OC) if the OCR is greater than 2; i.e., if the current load is lower than the historical maximum. In terms of a fine-grained soil’s response to a temperature variation in drained conditions, it has been largely demonstrated that the material contracts upon heating in NC conditions and a significant part of this deformation is irreversible, while highly OC materials experience a volume expansion during heating that is recovered during cooling. Between these two extreme cases, there is an intermediate case represented by slightly OC clays. In this case, the material shows initial dilation and subsequent contraction during heating, followed by contraction during cooling, thus representing a transition between the two main cases. The first experimental results of this nature date back to between the 1960s and 1980s [CAM 68, PLU 69, DEM 82, DES 88, BAL 88] and have been widely confirmed more recently [MIL 92, TOW 93, BUR 00, CEK 04]. Similar results have been obtained by the authors for a wide range of different clayey materials containing variable quantities of illite, kaolinite, chlorite and smectite. Some examples are given in Figure 1.2. In other words, these experimental results show that a soil can undergo irreversible deformation due to an increase in temperature under a constant mechanical load equal to (see NC cases in Figure 1.2) or even slightly lower than the preconsolidation stress (see cases with OCR = 2 in Figure 1.2). A number of experimental studies on various clays have been performed to develop a theoretical framework for describing this phenomenon, and have led to the conclusion that the “apparent” preconsolidation stress decreases at constant void ratio with increasing temperature. The word “apparent” is used to underline the fact that the applied mechanical load does not change, so that the maximum load historically applied is always the same. Some of these results are summarized and compared in Figure 1.3.

Figure 1.2. Thermal deformation of various clays under different initial conditions

Figure 1.3. Influence of temperature on preconsolidation pressure [LAL 03]

To fit these results within a theoretical-schematized framework, the evolution of the apparent preconsolidation pressure can be plotted in the mean effective stress-temperature plane, as shown in Figure 1.4, where the mean effective stress p′ is defined as:

[1.5]

The isotropic preconsolidation pressure, or the maximum mean effective stress that the soil has ever supported, is considered in this plane. As discussed earlier, and in light of the results illustrated so far, the (apparent) preconsolidation pressure represents the limit between the elastic and elastoplastic domains. In Figure 1.4, point A represents the state of a material subjected to an initial temperature (T₀) and an OC stress state, as its current mechanical load (p′_A) is lower than the preconsolidation pressure (p′_prec). If this material is subjected to drained heating under a constant ...

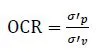
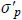
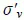
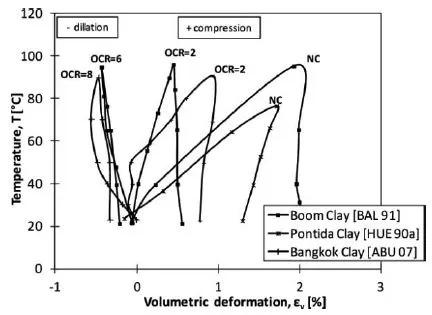
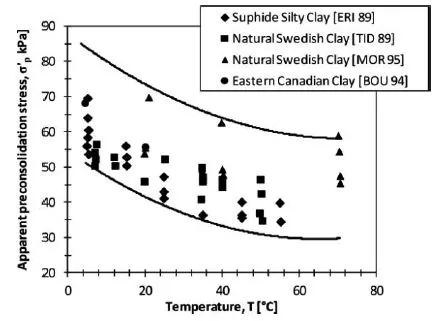
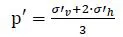
Table of contents

• Cover
• Contents
• Title Page
• Copyright
• Preface
• PART 1: Physical Modeling of Energy Piles at Different Scales
• PART 2: Numerical Modeling of Energy Geostructures
• PART 3: Engineering Practice
• List of Authors
• Index