Vibrations and Waves

George C. King

• Publisher: Wiley
• Year: 2013
• Print ISBN: 9780470011898, 9780470011881
• eBook ISBN: 9781118681787
• Edition: 1
• Topic: Physical Sciences
• Subtopic: Physics
• Index: Physics

This introductory text emphasises physical principles, rather than the mathematics. Each topic begins with a discussion of the physical characteristics of the motion or system. The mathematics is kept as clear as possible, and includes elegant mathematical descriptions where possible. Designed to provide a logical development of the subject, the book is divided into two sections, vibrations followed by waves. A particular feature is the inclusion of many examples, frequently drawn from everyday life, along with more cutting-edge ones. Each chapter includes problems ranging in difficulty from simple to challenging and includes hints for solving problems. Numerous worked examples included throughout the book.

1

Simple Harmonic Motion

In the physical world there are many examples of things that vibrate or oscillate, i.e. perform periodic motion. Everyday examples are a swinging pendulum, a plucked guitar string and a car bouncing up and down on its springs. The most basic form of periodic motion is called simple harmonic motion (SHM). In this chapter we develop quantitative descriptions of SHM. We obtain equations for the ways in which the displacement, velocity and acceleration of a simple harmonic oscillator vary with time and the ways in which the kinetic and potential energies of the oscillator vary. To do this we discuss two particularly important examples of SHM: a mass oscillating at the end of a spring and a swinging pendulum. We then extend our discussion to electrical circuits and show that the equations that describe the movement of charge in an oscillating electrical circuit are identical in form to those that describe, for example, the motion of a mass on the end of a spring. Thus if we understand one type of harmonic oscillator then we can readily understand and analyse many other types. The universal importance of SHM is that to a good approximation many real oscillating systems behave like simple harmonic oscillators when they undergo oscillations of small amplitude. Consequently, the elegant mathematical description of the simple harmonic oscillator that we will develop can be applied to a wide range of physical systems.

1.1 PHYSICAL CHARACTERISTICS OF SIMPLE HARMONIC OSCILLATORS

Observing the motion of a pendulum can tell us a great deal about the general characteristics of SHM. We could make such a pendulum by suspending an apple from the end of a length of string. When we draw the apple away from its equilibrium position and release it we see that the apple swings back towards the equilibrium position. It starts off from rest but steadily picks up speed. We notice that it overshoots the equilibrium position and does not stop until it reaches the other extreme of its motion. It then swings back toward the equilibrium position and eventually arrives back at its initial position. This pattern then repeats with the apple swinging backwards and forwards periodically. Gravity is the restoring force that attracts the apple back to its equilibrium position. It is the inertia of the mass that causes it to overshoot. The apple has kinetic energy because of its motion. We notice that its velocity is zero when its displacement from the equilibrium position is a maximum and so its kinetic energy is also zero at that point. The apple also has potential energy. When it moves away from the equilibrium position the apple’s vertical height increases and it gains potential energy. When the apple passes through the equilibrium position its vertical displacement is zero and so all of its energy must be kinetic. Thus at the point of zero displacement the velocity has its maximum value. As the apple swings back and forth there is a continuous exchange between its potential and kinetic energies. These characteristics of the pendulum are common to all simple harmonic oscillators: (i) periodic motion; (ii) an equilibrium position; (iii) a restoring force that is directed towards this equilibrium position; (iv) inertia causing overshoot; and (v) a continuous flow of energy between potential and kinetic. Of course the oscillation of the apple steadily dies away due to the effects of dissipative forces such as air resistance, but we will delay the discussion of these effects until Chapter 2.

1.2 A MASS ON A SPRING

1.2.1 A mass on a horizontal spring

Our first example of a simple harmonic oscillator is a mass on a horizontal spring as shown in Figure 1.1. The mass is attached to one end of the spring while the other end is held fixed. The equilibrium position corresponds to the unstretched length of the spring and x is the displacement of the mass from the equilibrium position along the x-axis. We start with an idealised version of a real physical situation. It is idealised because the mass is assumed to move on a frictionless surface and the spring is assumed to be weightless. Furthermore because the motion is in the horizontal direction, no effects due to gravity are involved. In physics it is quite usual to start with a simplified version or model because real physical situations are normally complicated and hard to handle. The simplification makes the problem tractable so that an initial, idealised solution can be obtained. The complications, e.g. the effects of friction on the motion of the oscillator, are then added in turn and at each stage a modified and improved solution is obtained. This process invariably provides a great deal of physical understanding about the real system and about the relative importance of the added complications.

Figure 1.1 A simple harmonic oscillator consisting of a mass m on a horizontal spring.

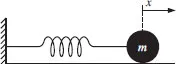
Figure 1.2 Variation of displacement x with time t for a mass undergoing SHM.

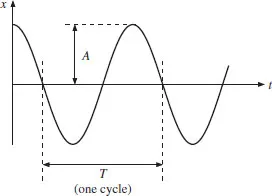
Experience tells us that if we pull the mass so as to extend the spring and then release it, the mass will move back and forth in a periodic way. If we plot the displacement x of the mass with respect to time t we obtain a curve like that shown in Figure 1.2. The amplitude of the oscillation is A, corresponding to the maximum excursion of the mass, and we ...

Table of contents

• Cover
• Contents
• Series page
• Title page
• Copyright page
• Dedication
• Editors’ Preface to the Manchester Physics Series
• Author’s Preface
• 1 Simple Harmonic Motion
• 2 The Damped Harmonic Oscillator
• 3 Forced Oscillations
• 4 Coupled Oscillators
• 5 Travelling Waves
• 6 Standing Waves
• 7 Interference and Diffraction of Waves
• 8 The Dispersion of Waves
• Appendix: Solutions to Problems
• Index