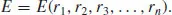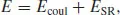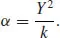Computational Approaches to Energy Materials

Richard Catlow, Alexey Sokol, Aron Walsh, Richard Catlow, Alexey Sokol, Aron Walsh

• Publisher: Wiley
• Year: 2013
• Print ISBN: 9781119950936
• eBook ISBN: 9781118551448
• Edition: 1
• Topic: Physical Sciences
• Subtopic: Physical & Theoretical Chemistry

The development of materials for clean and efficient energy generation and storage is one of the most rapidly developing, multi-disciplinary areas of contemporary science, driven primarily by concerns over global warming, diminishing fossil-fuel reserves, the need for energy security, and increasing consumer demand for portable electronics. Computational methods are now an integral and indispensable part of the materials characterisation and development process.  

Computational Approaches to Energy Materials presents a detailed survey of current computational techniques for the development and optimization of energy materials, outlining their strengths, limitations, and future applications.  The review of techniques includes current methodologies based on electronic structure, interatomic potential and hybrid methods. The methodological components are integrated into a comprehensive survey of applications, addressing the major themes in energy research.

Topics covered include:

• Introduction to computational methods and approaches
• Modelling materials for energy generation applications: solar energy and nuclear energy
• Modelling materials for storage applications: batteries and hydrogen
• Modelling materials for energy conversion applications: fuel cells, heterogeneous catalysis and solid-state lighting
• Nanostructures for energy applications

This full colour text is an accessible introduction for newcomers to the field, and a valuable reference source for experienced researchers working on computational techniques and their application to energy materials.

1

Computational Techniques

C. Richard A. Catlow1, Alexey A. Sokol1, and Aron Walsh2

1Department of Chemistry, University College London, London, UK

2 Department of Chemistry, University of Bath, Bath, UK

1.1 Introduction

In this chapter, we introduce fundamental approaches and ideas, which will be exploited in the rest of the book. These can be divided into two main streams: one dealing with the motion of atoms or ions described at a simplified level of theory and another focusing on electrons. The modeling framework, which covers both streams, is outlined next.

1.2 Atomistic Simulations

1.2.1 Basic Concepts

Methods based on interatomic potentials have a major and continuing role in molecular and materials simulation. The concept of the potential is simple: the energy (E) of the system is written as either an analytical or possibly a numerical function of the nuclear coordinates, ri, of particles i = 1 to n:

The function will normally be written as a sum of terms that depend on the coordinates of two, three or more atoms, although in many potential models, especially those for ionic and semi-ionic solids, only two body terms are considered; for the latter class of material, the electrostatic term is normally separated, that is,

where the Coulomb energy, Ecoul, is obtained by summing over all the interactions between the atomic charges, which are a parameter of the model and must be assigned. The short-range energy, ESR, represents the remainder of the interactions including Pauli repulsion and covalent and dispersive attractive terms. Simple analytical functions are commonly used for ESR, including inverse power (r−m) and exponential terms (exp(−r/r0). Detailed discussions can be found in the seminal book of Born and Huang [1], and more recent literature [2,3].

In modeling metallic systems, rather different approaches must be adopted; in particular, the effects of the conduction band electrons on atomic interactions must be included—a difficult problem for which there is no simple solution. Nevertheless, a number of effective and useful potential models have been developed for metallic systems, which may be based on the “embedded atom concept.” Details and examples are given in [4].

Accurate models especially for ionic solids must include a representation of polarization. It has long been known that in solid-state modeling simple point dipole models have serious inadequacies, leading to excessive polarization, as they omit any representation of the damping of polarization by the resulting increase in short-range repulsion with neighboring ions. This problem was simply and elegantly solved by the development over 50 years ago of the shell model by Dick and Overhauser [5]. This crude but effective model describes an atom or ion in terms of a “core,” which contains all the mass and represents the nucleus and core electrons, and a “shell” (of charge, Y), which is massless and represents the polarizable valence shell electrons; the core and the shell are coupled by an harmonic spring (of constant, k), and the development of a dipole moment is modeled by the displacement of the shell relative to the core. The charge of the shell (Y) and the value of the spring constant (k) are parameters of the model; and of course, the sum of core and shell charges must equal the total atomic charge. Moreover, the shell model parameters can be related to the polarizability (α) by the simple relationship:

Elaborations such as the “breathing shell” model have been developed, but the basic shell model remains the most widely used treatment of polarizability in materials simulation.

A potential model will normally therefore consist of (i) a set of atomic charges, where appropriate, (ii) analytical (or occasionally numerical) functions, containing variable parameters, and (iii) a representation of polarizability for short-range interactions, which will require specification of the parameters Y and k when the shell model is used. In Section 1.2.2, we review the methods used to set the variable parameters and then we return to some of the more common potential models.

1.2.2 Parameterization

Once the choice of the form of the potential model has been made, the crucial next step is to parameterize the model, that is, fix the variable parameters, so that the model describes the specific material (or materials) under investigation. Here, there are two broad strategies, which may in some cases be used in concert:

1. Empirical fitting: involves variation of the parameters in order to reproduce, as accurately as possible, experimental data of the material. Standard procedures are available for calculating a wide range of properties using potential models (see, e.g., [3]). These are usually coupled to a least-squares minimization procedure to achieve the best fit of calculated to experimental data. Commonly used data include cohesive or lattice energies, crystal structures, elastic and dielectric properties and where available lattice dynamical data. The procedure is simple in concept and highly automated in principle, but in practice it may prove difficult and lengthy and require extensive user intervention and direction to achieve the optimum parameter set. And, of course, it requires that suitable and accurate experimental data be available.

2. Fitting to energy surfaces: requires no empirical data, but rather uses energy surfaces calculated by electronic structure methods, with parameters in the potential model being varied to ensure that the surface calculated using the potential model matches as closely as possible that determined by the electronic structure technique. The energy surface is constructed by varying the structural parameters of the material or molecule in a systematic manner, followed by a least squares fitting of the potential parameters. The approach is again in principle straightforward but of course requires an accurate energy surface to which to fit the potential parameters.

Both approaches are widely used and as noted they may be used together, and indeed a potential derived by the latter approach should always be tested in regards to the extent to which it reproduces any available experimental data. More generally, in evaluating a potential model, it is necessary to examine carefully its mode of derivation. When empirical methods are used, the range and accuracy of the data will be crucial; when parameters have been derived from calculated energy surfaces at a higher level of theory, the quality of electronic structure technique will determine the accuracy of the parameterized model.

1.2.3 Parameter Sets

A wide range of parameter sets are available for different classes of material and many can be found in online databases [6]. For oxides, which are extensively used in energy materials, the Born model parameter set derived by Catlow and Lewis [7] may often provide a useful starting point as these parameters have the merit of simplicity and transferability between different materials, which may be an important factor in assessing the suitability of a potential model for applications, in which several materials are investigated and compared. Other significant considerations when deciding on the suitability of a model are accuracy—that is, the extent to which the model reproduces known crystal properties—and stability—an important consideration as models may perform well around the equilibrium configuration of a crystal but have instabilities for other configurations that may be sampled in dynamical simulations or simulations of defective crystals. More generally the assessment and choice of a potential model is crucially important and needs careful and detailed consideration.

1.2.4 Implementation

Having developed or chosen a suitable model for calculating energies and forces as a function of nuclear coordinates, they may be implemented in a wide range of powerful simulation tools (e.g., CP2K, DL-POLY, GULP, GROMACS, KLMC, LAMMPS, METADISE), based on three main concepts:

1. Minimization: A conceptually simple approach, in which the aim is to locate the energy minimum configuration of the system modeled, with the energy calculated using an interatomic potential model or by an electronic structure technique. The complexity of energy landscapes may, however, make the identification of the global minimum far from straightforward, and a range of both sophisticated search and minimization algorithms have been developed. Minimization is perhaps at its most effective when refining approximately known structures, although developments in search procedures for energy landscapes have given the techniques an increasingly predictive value [8,9]. Minimization may be applied to any type of atomic assembly including crystals, molecules and adsorbed species. The approach has been applied with particular effect to defects in solids where the method, originally pioneered by Mott [10], effectively minimizes the energy of a region of crystal surrounding the defect with more approximate quasi-continuum treatments of the more distant regions of the lattice. Energy minimization may also be extended to free energy minimization when entropies can be calculated by, for example, the vibrational partition function in a crystalline solid [11]. The technique has been further developed to study transition states, or more generally, minimum energy pathways as in the popular nudged-elastic band (NEB) approach. Overall, despite its basic simplicity and obvious limitations in omitting any explicit representations of dynamic effects, minimization is a robust and powerful approach and should often be the first approach of a simulation study.

2. Molecular Dyna...

Table of contents

• Cover
• Title Page
• Copyright
• About the Editors
• List of Contributors
• Preface
• Acknowledgments
• Chapter 1: Computational Techniques
• Chapter 2: Energy Generation: Solar Energy
• Chapter 3: Energy Generation: Nuclear Energy
• Chapter 4: Energy Storage: Rechargeable Lithium Batteries
• Chapter 5: Energy Storage: Hydrogen
• Chapter 6: Energy Conversion: Solid Oxide Fuel Cells
• Chapter 7: Energy Conversion: Heterogeneous Catalysis
• Chapter 8: Energy Conversion: Solid-State Lighting
• Chapter 9: Toward the Nanoscale
• Further Reading
• Index